Exponential Distribution
Overview
The exponential distribution is a one-parameter family of curves. The exponential distribution models wait times when the probability of waiting an additional period of time is independent of how long you have already waited. For example, the probability that a light bulb will burn out in its next minute of use is relatively independent of how many minutes it has already burned.
Statistics and Machine Learning Toolbox™ offers several ways to work with the exponential distribution.
Create a probability distribution object
ExponentialDistributionby fitting a probability distribution to sample data (fitdist) or by specifying parameter values (makedist). Then, use object functions to evaluate the distribution, generate random numbers, and so on.Work with the exponential distribution interactively by using the Distribution Fitter app. You can export an object from the app and use the object functions.
Use distribution-specific functions (
expcdf,exppdf,expinv,explike,expstat,expfit,exprnd) with specified distribution parameters. The distribution-specific functions can accept parameters of multiple exponential distributions.Use generic distribution functions (
cdf,icdf,pdf,random) with a specified distribution name ('Exponential') and parameters.
Parameters
The exponential distribution uses the following parameter.
| Parameter | Description | Support |
|---|---|---|
mu (μ) | Mean | μ > 0 |
The parameter μ is also equal to the standard deviation of the exponential distribution.
The standard exponential distribution has μ=1.
A common alternative parameterization of the exponential distribution is to use λ defined as the mean number of events in an interval as opposed to μ, which is the mean wait time for an event to occur. λ and μ are reciprocals.
Parameter Estimation
The likelihood function is the probability density
function (pdf) viewed as a function of the parameters. The maximum
likelihood estimates (MLEs) are the parameter estimates that
maximize the likelihood function for fixed values of
x.
The maximum likelihood estimator of μ for the exponential distribution is , where is the sample mean for samples x1, x2, …, xn. The sample mean is an unbiased estimator of the parameter μ.
To fit the exponential distribution to data and find a parameter estimate, use
expfit, fitdist, or mle. Unlike
expfit and mle, which return
parameter estimates, fitdist returns the fitted probability
distribution object ExponentialDistribution. The object
property mu stores the parameter estimate.
For an example, see Fit Exponential Distribution to Data.
Probability Density Function
The pdf of the exponential distribution is
For an example, see Compute Exponential Distribution pdf.
Cumulative Distribution Function
The cumulative distribution function (cdf) of the exponential distribution is
The result p is the probability that a single observation from the exponential distribution with mean μ falls in the interval [0, x].
For an example, see Compute Exponential Distribution cdf.
Inverse Cumulative Distribution Function
The inverse cumulative distribution function (icdf) of the exponential distribution is
The result x is the value such that an observation from an exponential distribution with parameter μ falls in the range [0 x] with probability p.
Hazard Function
The hazard function (instantaneous failure rate) is the ratio of the pdf and the complement of the cdf. If f(t) and F(t) are the pdf and cdf of a distribution (respectively), then the hazard rate is . Substituting the pdf and cdf of the exponential distribution for f(t) and F(t) yields a constant λ. The exponential distribution is the only continuous distribution with a constant hazard function. λ is the reciprocal of μ and can be interpreted as the rate at which events occur in any given interval. Consequently, when you model survival times, the probability that an item will survive an extra unit of time is independent of the current age of the item.
For an example, see Exponentially Distributed Lifetimes.
Examples
Fit Exponential Distribution to Data
Generate a sample of 100 of exponentially distributed random numbers with mean 700.
x = exprnd(700,100,1); % Generate sampleFit an exponential distribution to data using fitdist.
pd = fitdist(x,'exponential')pd =
ExponentialDistribution
Exponential distribution
mu = 641.934 [532.598, 788.966]
fitdist returns an ExponentialDistribution object. The interval next to the parameter estimate is the 95% confidence interval for the distribution parameter.
Estimate the parameter using the distribution functions.
[muhat,muci] = expfit(x) % Distribution specific functionmuhat = 641.9342
muci = 2×1
532.5976
788.9660
[muhat2,muci2] = mle(x,'distribution','exponential') % Generic distribution function
muhat2 = 641.9342
muci2 = 2×1
532.5976
788.9660
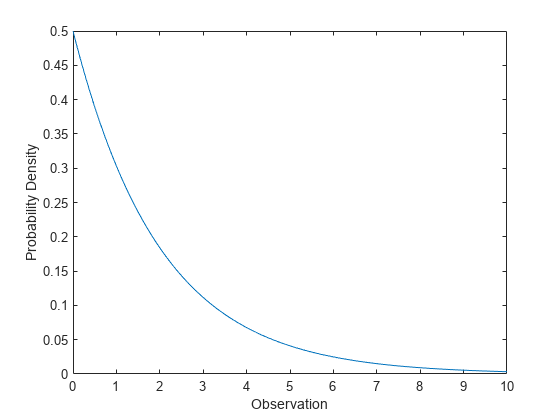
Compute Exponential Distribution pdf
Compute the pdf of an exponential distribution with parameter mu = 2.
x = 0:0.1:10; y = exppdf(x,2);
Plot the pdf.
figure; plot(x,y) xlabel('Observation') ylabel('Probability Density')
Compute Exponential Distribution cdf
Compute the cdf of an exponential distribution with parameter mu = 2.
x = 0:0.1:10; y = expcdf(x,2);
Plot the cdf.
figure; plot(x,y) xlabel('Observation') ylabel('Cumulative Probability')

Exponentially Distributed Lifetimes
Compute the hazard function of the exponential distribution with mean mu = 2 at the values one through five.
x = 1:5; lambda1 = exppdf(x,2)./(1-expcdf(x,2))
lambda1 = 1×5
0.5000 0.5000 0.5000 0.5000 0.5000
The hazard function (instantaneous rate of failure to survival) of the exponential distribution is constant and always equals 1/mu. This constant is often denoted by λ.
Evaluate the hazard functions of the exponential distributions with means one through five at x = 3.
mu = 1:5; lambda2 = exppdf(3,mu)./(1-expcdf(3,mu))
lambda2 = 1×5
1.0000 0.5000 0.3333 0.2500 0.2000
The probability that an item with an exponentially distributed lifetime survive one more unit of time is independent of how long it has survived.
Compute the probability of an item surviving one more year at various ages when the mean survival time is 10 years.
x2 = 5:5:25; x3 = x2 + 1; deltap = (expcdf(x3,10)-expcdf(x2,10))./(1-expcdf(x2,10))
deltap = 1×5
0.0952 0.0952 0.0952 0.0952 0.0952
The probability of surviving one more year is the same regardless of how long an item has already survived.
Related Distributions
Burr Type XII Distribution — The Burr distribution is a three-parameter continuous distribution. An exponential distribution compounded with a gamma distribution on the mean yields a Burr distribution.
Gamma Distribution — The gamma distribution is a two-parameter continuous distribution that has parameters a (shape) and b (scale). When a = 1, the gamma distribution is equal to the exponential distribution with mean μ = b. The sum of k exponentially distributed random variables with mean μ has a gamma distribution with parameters a = k and μ = b.
Geometric Distribution — The geometric distribution is a one-parameter discrete distribution that models the total number of failures before the first success in repeated Bernoulli trials. The geometric distribution is a discrete analog of the exponential distribution and is the only discrete distribution with a constant hazard function.
Generalized Pareto Distribution — The generalized Pareto distribution is a three-parameter continuous distribution that has parameters k (shape), σ (scale), and θ (threshold). When both k = 0 and θ = 0, the generalized Pareto distribution is equal to the exponential distribution with mean μ = σ.
Poisson Distribution — The Poisson distribution is a one-parameter discrete distribution that takes nonnegative integer values. The parameter λ is both the mean and the variance of the distribution. The Poisson distribution models counts of the number of times a random event occurs in a given amount of time. In such a model, the amount of time between occurrences is modeled by the exponential distribution with mean .
Weibull Distribution — The Weibull distribution is a two-parameter continuous distribution that has parameters a (scale) and b (shape). The Weibull distribution is also used to model lifetimes, but it does not have a constant hazard rate. When b = 1, the Weibull distribution is equal to the exponential distribution with mean μ = a.
For an example, see Compare Exponential and Weibull Distribution Hazard Functions.
References
[1] Crowder, Martin J., ed. Statistical Analysis of Reliability Data. Reprinted. London: Chapman & Hall, 1995.
[2] Kotz, Samuel, and Saralees Nadarajah. Extreme Value Distributions: Theory and Applications. London : River Edge, NJ: Imperial College Press; Distributed by World Scientific, 2000.
[3] Meeker, William Q., and Luis A. Escobar. Statistical Methods for Reliability Data. Wiley Series in Probability and Statistics. Applied Probability and Statistics Section. New York: Wiley, 1998.
[4] Lawless, Jerald F. Statistical Models and Methods for Lifetime Data. 2nd ed. Wiley Series in Probability and Statistics. Hoboken, N.J: Wiley-Interscience, 2003.
See Also
ExponentialDistribution | expcdf | exppdf | expinv | explike | expstat | expfit | exprnd | makedist | fitdist
