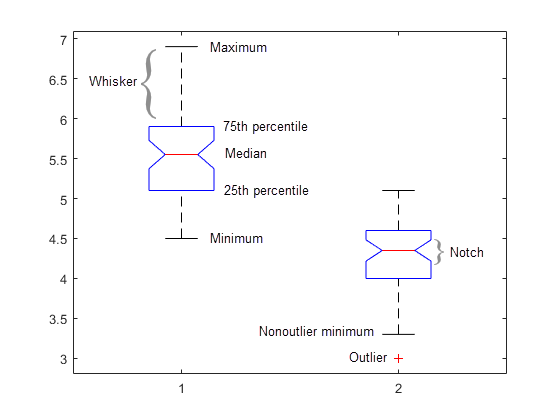
boxplot
要約統計量を箱ひげ図で可視化
説明
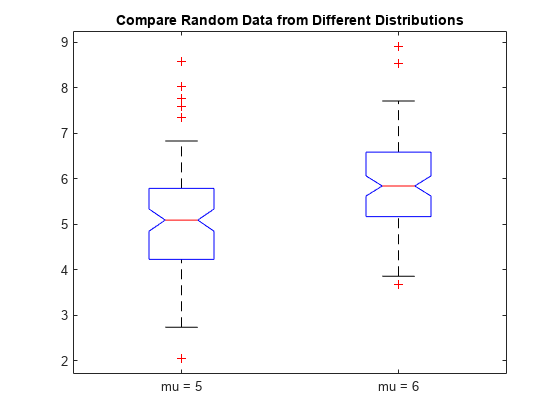
boxplot( は、x)x 内のデータの箱ひげ図を作成します。x がベクトルの場合、boxplot は 1 つのボックスをプロットします。x が行列の場合、boxplot は x の各列について 1 つずつボックスをプロットします。
各ボックスにおいて、中央の印は中央値を、ボックスの上下の端はそれぞれ 25 番目と 75 番目の百分位数を示します。ひげは、外れ値とは見なされない最も極端なデータ点まで延びます。外れ値は、'+' マーカー記号を使用して個別にプロットされます。
boxplot( は、前の構文のいずれかを使用し、axes グラフィックス オブジェクト ax,___)ax で指定された座標軸を使用して箱ひげ図を作成します。
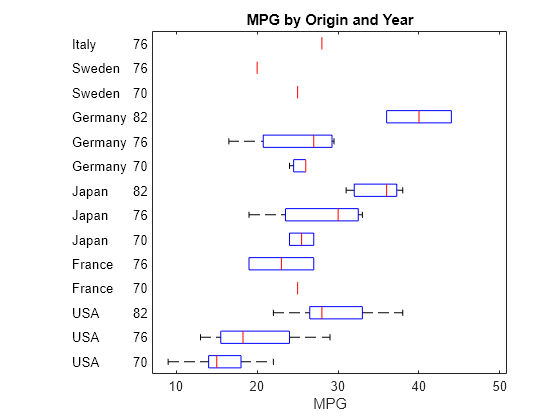
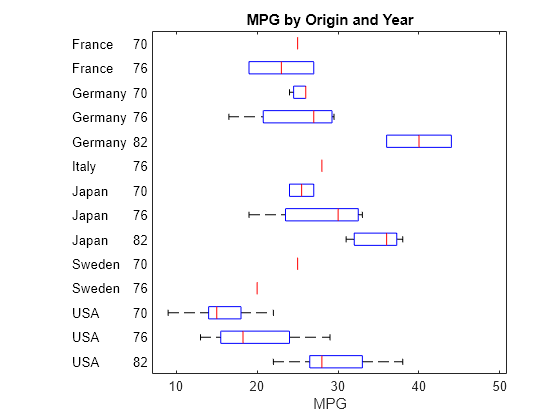
boxplot(___, は、1 つ以上の Name,Value)Name,Value ペア引数で指定された追加オプションを使用して箱ひげ図を作成します。たとえば、ボックスのスタイルや順序を指定できます。
例
標本データを読み込みます。
load carsmallガロンあたりの走行マイル数 (MPG) の測定値から箱ひげ図を作成します。タイトルを追加して軸のラベルを設定します。
boxplot(MPG) xlabel('All Vehicles') ylabel('Miles per Gallon (MPG)') title('Miles per Gallon for All Vehicles')
この箱ひげ図は、標本データに含まれているすべての自動車についてガロンあたりの走行マイル数の中央値が約 24 であることを示しています。最小値は約 9、最大値は約 44 です。
標本データを読み込みます。
load carsmall標本データのガロンあたりの走行マイル数 (MPG) の測定値を自動車の生産国 (Origin) 別にグループ化して箱ひげ図を作成します。タイトルを追加して軸のラベルを設定します。
boxplot(MPG,Origin) title('Miles per Gallon by Vehicle Origin') xlabel('Country of Origin') ylabel('Miles per Gallon (MPG)')
各ボックスは、特定の国の自動車の MPG データを視覚的に表しています。Italy のボックスが単一の線として表示されているのは、このグループの観測値が標本データに 1 つしか含まれていないためです。
2 組の標本データを作成します。最初の標本 x1 は、mu = 5、sigma = 1 の正規分布から生成された乱数を含んでいます。2 番目の標本 x2 は、mu = 6、sigma = 1 の正規分布から生成された乱数を含んでいます。
rng default % For reproducibility x1 = normrnd(5,1,100,1); x2 = normrnd(6,1,100,1);
x1 と x2 のノッチのある箱ひげ図を作成します。各ボックスに、対応する mu 値でラベルを設定します。
figure boxplot([x1,x2],'Notch','on','Labels',{'mu = 5','mu = 6'}) title('Compare Random Data from Different Distributions')
この箱ひげ図は、2 つのグループの中央値の差が約 1 であることを示しています。箱ひげ図でノッチが重なっていないので、95% の信頼度で真の中央値が異なると結論付けることができます。
次の図は、ひげの最大長を四分位数間範囲の 1.0 倍に指定した、同じデータの箱ひげ図を示しています。ひげの範囲外にあるデータ点は、+ を使用して示されています。
figure boxplot([x1,x2],'Notch','on','Labels',{'mu = 5','mu = 6'},'Whisker',1) title('Compare Random Data from Different Distributions')
ひげを短くすると、boxplot はより多くのデータ点を外れ値として表示します。
標本データとして使用するために、標準正規分布から生成された 100 行 25 列の乱数の行列を作成します。
rng default % For reproducibility x = randn(100,25);
同じ図に x のデータの 2 つの箱ひげ図を作成します。上のプロットでは既定の書式設定を、下のプロットではコンパクトな書式設定を使用します。
figure subplot(2,1,1) boxplot(x) subplot(2,1,2) boxplot(x,'PlotStyle','compact')
各プロットは同じデータを表していますが、ボックス数が多いプロットではコンパクトな書式設定の方が可読性が向上する可能性があります。
グループ化されたデータを使用して箱ひげ図を作成します。データ グループの順序を指定して、箱ひげ図の順序を変更します。
100 台の自動車の測定値を含む carsmall データ セットを読み込みます。
load carsmallガロンあたりの走行マイル数 (MPG) の値から箱ひげ図を作成します。自動車の生産国とモデル年に基づいてデータをグループ化します。グループ ラベルが見やすくなるように、箱ひげ図を横方向にします。
groupingVariables = {Origin,Model_Year};
boxplot(MPG,groupingVariables,"Orientation","horizontal")
xlabel("MPG")
title("MPG by Origin and Year")
carsmall データ セットには、生産国とモデル年のすべての組み合わせに対応する自動車は含まれていません。たとえば、このデータ セットには、1970 年にイタリアで生産された自動車は含まれていません。
名前と値の引数 GroupOrder を使用して、箱ひげ図の順序を変更します。データ セット内の各グループの順序を指定します。コンマを使用して、異なるグループ化変数の値を区切ります。
groupOrder = ["USA,82","USA,76","USA,70","Sweden,76","Sweden,70", ... "Japan,82","Japan,76","Japan,70","Italy,76","Germany,82", ... "Germany,76","Germany,70","France,76","France,70"]; boxplot(MPG,groupingVariables,"Orientation","horizontal", ... "GroupOrder",groupOrder) xlabel("MPG") title("MPG by Origin and Year")
生産国が上からアルファベット順になり、各国のモデル年が上から昇順になりました。
グループ化変数を使用して、長さが異なる複数のデータ ベクトルの箱ひげ図を作成します。
長さが異なる 3 つの列ベクトルを無作為に生成します。長さは、それぞれ 5、10、15 にします。データを結合して、長さが 30 である単一の列ベクトルにします。
rng('default') % For reproducibility x1 = rand(5,1); x2 = rand(10,1); x3 = rand(15,1); x = [x1; x2; x3];
グループ化変数を作成し、x 内の同じベクトルに対応する行に同じ値を割り当てます。たとえば、x の最初の 5 行はすべて同じベクトル x1 に由来するので、g の最初の 5 行は同じ値 First になります。
g1 = repmat({'First'},5,1);
g2 = repmat({'Second'},10,1);
g3 = repmat({'Third'},15,1);
g = [g1; g2; g3];箱ひげ図を作成します。
boxplot(x,g)
入力引数
名前と値の引数
オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。
R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。
例: 'Notch','on','Labels',{'mu = 5','mu = 6'} は、ノッチのある箱ひげ図を作成し、左から右の順で 2 つのボックスに mu = 5 および mu = 6 というラベルを付けます。
ボックスの外観
ボックスのスタイル。次のいずれかとして指定します。
| 名前 | 値 |
|---|---|
'outline' | 点線のひげを使用して、塗りつぶされていないボックスをプロットします。これは、'PlotStyle' が 'traditional' の場合の既定設定です。 |
'filled' | 実線のひげを使用して、塗りつぶされた幅の狭いボックスをプロットします。これは、'PlotStyle' が 'compact' の場合の既定設定です。 |
例: 'BoxStyle','filled'
ボックスの色。RGB 3 成分、文字ベクトル、または string スカラーとして指定します。RGB 3 成分は、各要素がそれぞれ色の赤、緑および青の成分の強度を指定する 3 要素の行ベクトルです。各強度は、[0,1] の範囲内でなければなりません。
次の表に、使用可能な色指定文字および対応する RGB 3 成分の値を示します。
| 完全名 | 省略名 | RGB 3 成分 |
|---|---|---|
| 黄 | 'y' | [1 1 0] |
| 赤紫 | 'm' | [1 0 1] |
| シアン | 'c' | [0 1 1] |
| 赤 | 'r' | [1 0 0] |
| 緑 | 'g' | [0 1 0] |
| 青 | 'b' | [0 0 1] |
| 白 | 'w' | [1 1 1] |
| 黒 | 'k' | [0 0 0] |
複数の色は、文字ベクトルまたは string スカラーによる色の名前 ('rgbm' など)、または RGB 値による 3 列の行列によって指定できます。この並びは必要に応じて複製されるか打ち切られるので、たとえば 'rb' を指定すると、赤と青のボックスが交互にプロットされます。
名前と値のペアの引数 'ColorGroup' を指定しなかった場合、boxplot はすべてのボックスについて同じ配色を使用します。
例: 'Colors','rgbm'
中央値のスタイル。次のいずれかとして指定します。
| 名前 | 値 |
|---|---|
'line' | 中央値を表す線を各ボックスに描画します。'PlotStyle' が 'traditional' の場合、これが既定値になります。 |
'target' | 中央値を表す白い円内の黒い点を各ボックスに描画します。'PlotStyle' が 'compact' の場合、これが既定値になります。 |
例: 'MedianStyle','target'
比較区間のマーカー。次のいずれかとして指定します。
| 名前 | 値 |
|---|---|
'off' | ボックスの表示から比較区間を省きます。 |
'on' | 'PlotStyle' が 'traditional' の場合、ノッチを使用して比較区間を描画します。'PlotStyle' が 'compact' の場合、三角形のマーカーを使用して比較区間を描画します。 |
'marker' | 三角形のマーカーを使用して比較区間を描画します。 |
区間が重なっていない場合、2 つの中央値は有意水準 5% で有意差があります。boxplot は、ノッチの両端または三角形のマーカーの中心を使用して区間の両端点を表します。端は q2 – 1.57(q3 – q1)/sqrt(n) と q2 + 1.57(q3 – q1)/sqrt(n) に対応します。ここで、q2 は中央値 (50 番目の百分位数)、q1 と q3 はそれぞれ 25 番目と 75 番目の百分位数、n は NaN 値を除いた観測数です。標本サイズが小さい場合、ノッチがボックスの端を超えて伸びる可能性があります。
ノッチのある箱ひげ図のラベル付きの例については、箱ひげ図を参照してください。
例: 'Notch','on'
外れ値のマーカー サイズ。正の数値として指定します。指定された値は、ポイント単位のマーカー サイズを表します。
'PlotStyle' が 'traditional' の場合、OutlierSize の既定値は 6 になります。'PlotStyle' が 'compact' の場合、OutlierSize の既定値は 4 になります。
例: 'OutlierSize',8
データ型: single | double
プロットのスタイル。次のいずれかとして指定します。
| 名前 | 値 |
|---|---|
'traditional' | 従来のボックス スタイルを使用してボックスをプロットします。 |
'compact' | グループ数が多いプロット用に設計されている、小さいボックス スタイルを使用してボックスをプロットします。このスタイルでは、他の一部のパラメーターの既定設定が変化します。 |
例: 'PlotStyle','compact'
外れ値のマーカーと色。マーカーと色の記号を含む文字ベクトルまたは string スカラーとして指定します。記号の順序に制限はありません。マーカーの記号を省略した場合、外れ値は表示されません。色の記号を省略した場合、外れ値はボックスと同じ色で表示されます。
'PlotStyle' が 'traditional' の場合、既定値は '+r' になり、赤いプラス記号 '+' マーカー記号が各外れ値のプロットに使用されます。
'PlotStyle' が 'compact' の場合、既定値は 'o' になり、対応するボックスと同じ色の円 'o' マーカー記号が各外れ値のプロットに使用されます。
| マーカー | 説明 | 結果として得られるマーカー |
|---|---|---|
"o" | 円 |
|
"+" | プラス記号 |
|
"*" | アスタリスク |
|
"." | 点 |
|
"x" | 十字 |
|
"_" | 水平線 |
|
"|" | 垂直線 |
|
"square" | 正方形 |
|
"diamond" | 菱形 |
|
"^" | 上向き三角形 |
|
"v" | 下向き三角形 |
|
">" | 右向き三角形 |
|
"<" | 左向き三角形 |
|
"pentagram" | 星形五角形 |
|
"hexagram" | 星形六角形 |
|
| 色 | 説明 |
|---|---|
| 黄 |
| 赤紫 |
| シアン |
| 赤 |
| 緑 |
| 青 |
| 白 |
| 黒 |
例: 外れ値を非表示にするには 'Symbol','' を指定します。
ボックスの幅。数値スカラーまたは数値ベクトルとして指定します。ボックスの数と異なる数の幅の値を指定した場合、必要に応じて値のリストが複製されるか打ち切られます。
この名前と値のペアの引数を指定しても、ボックス間の間隔は変化しません。したがって、大きい値の 'Widths' を指定した場合、ボックスが重なる可能性があります。
既定のボックスの幅は、ボックス間の最小分離の半分に等しくなります。名前と値のペアの引数 'Positions' で既定値を使用した場合、これは 0.5 になります。
例: 'Widths',0.3
データ型: single | double
グループの外観
データの範囲と最大距離
プロットの外観
詳細
箱ひげ図は、標本データの要約統計量を可視化します。これには、次のような特徴があります。
各ボックスの上下の線は、標本の 75 番目と 25 番目の百分位数です。各ボックスの上下間の距離は、四分位数間範囲を示しています。
各ボックスの中央の赤い線は、標本中央値です。中央値がボックスの中央に位置していない場合、そのプロットは標本歪度を示します。
ボックスの上下に延びている線がひげです。ひげは、四分位数間範囲の端から、ひげの長さ内にある最も遠い観測値 ("隣接値") まで描かれます。
ひげの長さを超える観測は、外れ値としてマークされています。既定の設定では、ボックスの上下から四分位数間範囲の 1.5 倍より大きく離れた値を外れ値としています。ただし、この値は追加の入力引数を使用して調整できます。外れ値は、赤い + 記号として表示されます。
ノッチは、標本間の中央値の変動性を示します。ノッチがオーバーラップしていない箱どうしが有意水準 5% で異なる中央値をもつように、ノッチの幅が計算されます。有意水準は正規分布の仮定に基づきますが、中央値の比較は他の分布に対して適度にロバストです。箱ひげ図の中央値を比較することは、平均に対して使われる t 検定に似ており、視覚による仮説検定のように考えられます。場合によっては、ノッチがボックスの外まで伸びることもあります。
ヒント
boxplotはデータの視覚的な表現を作成しますが、数値を返すわけではありません。標本データの関連する要約統計量を計算するには、次の関数を使用します。データ値とグループ名を参照するには、Figure ウィンドウ のデータ カーソルを使用します。カーソルは、
datalimパラメーターの影響を受ける元の値を表示します。外れ値が属するグループにラベルを付けるには、関数gnameを使用します。箱ひげ図のコンポーネントのグラフィックス プロパティを変更するには、
Tagプロパティを指定してfindobjを使用することによりコンポーネントのハンドルを取得します。箱ひげ図のコンポーネントのTag値は、パラメーター設定によって異なります。次の表を参照してください。パラメーター設定 Tag の値 すべて設定 'Box''Outliers'
'PlotStyle'が'traditional'である場合'Median''Upper Whisker''Lower Whisker''Upper Adjacent Value''Lower Adjacent Value'
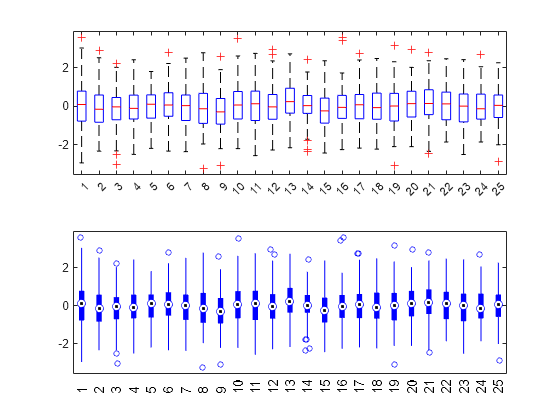
'PlotStyle'が'compact'である場合'Whisker''MedianOuter''MedianInner'
'Notch'が'marker'である場合'NotchLo''NotchHi'
代替機能
関数 boxchart を使用して BoxChart オブジェクトを作成することもできます。boxchart は boxplot の機能をすべて備えているわけではありませんが、いくつかの利点があります。関数 boxchart は、次の点が boxplot と異なります。
グループ軸に沿ってカテゴリカル ルーラーを使用できる
凡例のオプションが用意されている
hold onコマンドを使用できるノッチがより見やすいように改善された視覚的なデザインを備えている
このオブジェクトの外観と動作を制御するには、BoxChart のプロパティ を変更します。
参照
[1] McGill, R., J. W. Tukey, and W. A. Larsen. “Variations of Boxplots.” The American Statistician. Vol. 32, No. 1, 1978, pp. 12–16.
[2] Velleman, P.F., and D.C. Hoaglin. Applications, Basics, and Computing of Exploratory Data Analysis. Pacific Grove, CA: Duxbury Press, 1981.
[3] Nelson, L. S. “Evaluating Overlapping Confidence Intervals.” Journal of Quality Technology. Vol. 21, 1989, pp. 140–141.
[4] Langford, E. “Quartiles in Elementary Statistics”, Journal of Statistics Education. Vol. 14, No. 3, 2006.
バージョン履歴
R2006a より前に導入参考
anova1 | kruskalwallis | multcompare | min | max | median | quantile | iqr | grpstats
