このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

kruskalwallis

クラスカル・ワリス検定

構文

p = kruskalwallis(x)

p = kruskalwallis(x,group)

p = kruskalwallis(x,group,displayopt)

[p,tbl,stats] = kruskalwallis(___)

説明

p = kruskalwallis(x) は、クラスカル・ワリス検定を使用して、行列 x の各列のデータが同じ分布から派生しているという帰無仮説についての p 値を返します。対立仮説は、すべての標本が同じ分布から派生しているとは限らないとします。クラスカル・ワリス検定は、1 因子 ANOVA のノンパラメトリックな別バージョンを提供します。詳細については、クラスカル・ワリス検定を参照してください。

p = kruskalwallis(x,group) は、グループ化変数 group で指定された各カテゴリカル グループのデータが同じ分布から派生しているという帰無仮説の検定についての p 値を返します。対立仮説は、すべてのグループが同じ分布から派生しているとは限らないとします。

p = kruskalwallis(x,group,displayopt) は、検定の p 値を返し、ANOVA 表と箱ひげ図を表示または非表示にするかを選択できます。

[p,tbl,stats] = kruskalwallis(___) は、ANOVA 表の cell 配列 tbl と検定統計量に関する情報を含む stats 構造体も返します。

例

データの標本が同じ分布かどうか検定する

2 つの異なる正規確率分布オブジェクトを作成します。1 番目の分布は mu = 0 および sigma = 1 にします。2 番目の分布は mu = 2 および sigma = 1 にします。

pd1 = makedist('Normal');
pd2 = makedist('Normal','mu',2,'sigma',1);

これらの 2 つの分布から乱数を生成して標本データの行列を作成します。

rng('default'); % for reproducibility
x = [random(pd1,20,2),random(pd2,20,1)];

最初の分布から生成されたデータを x の最初の 2 列に格納し、2 番目の分布から生成されたデータを 3 列目に格納します。

x の各列の標本データが同じ分布から派生しているという帰無仮説を検定します。

p = kruskalwallis(x)

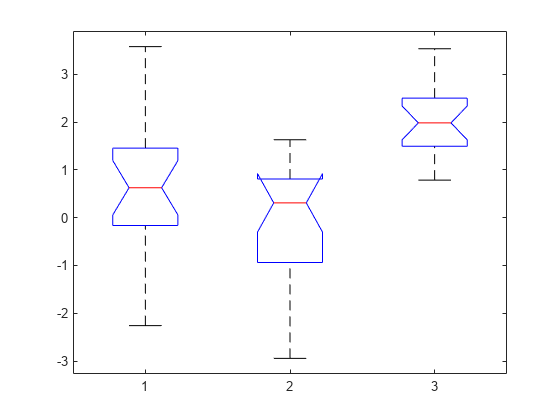
p = 
3.6896e-06

p の戻り値は、kruskalwallis が有意水準 1% で 3 つすべてのデータ標本が同じ分布から派生しているという帰無仮説を棄却することを示します。追加の検定結果を示す ANOVA 表と、x の各列の要約統計量を視覚的に示す箱ひげ図が表示されます。

中央値が同じでないかどうかを調べる補足の検定を実行する

2 つの異なる正規確率分布オブジェクトを作成します。1 番目の分布は mu = 0 および sigma = 1 にします。2 番目の分布は mu = 2 および sigma = 1 にします。

pd1 = makedist('Normal');
pd2 = makedist('Normal','mu',2,'sigma',1);

これらの 2 つの分布から乱数を生成して標本データの行列を作成します。

rng('default'); % for reproducibility
x = [random(pd1,20,2),random(pd2,20,1)];

最初の分布から生成されたデータを x の最初の 2 列に格納し、2 番目の分布から生成されたデータを 3 列目に格納します。

x の各列の標本データが同じ分布から派生しているという帰無仮説を検定します。出力は非表示にし、追加の検定で使用する stats 構造体を生成します。

[p,tbl,stats] = kruskalwallis(x,[],'off')

p = 
3.6896e-06

tbl=4×6 cell array
    {'Source' }    {'SS'        }    {'df'}    {'MS'        }    {'Chi-sq'  }    {'Prob>Chi-sq'}
    {'Columns'}    {[7.6311e+03]}    {[ 2]}    {[3.8155e+03]}    {[ 25.0200]}    {[ 3.6896e-06]}
    {'Error'  }    {[1.0364e+04]}    {[57]}    {[  181.8228]}    {0×0 double}    {0×0 double   }
    {'Total'  }    {[     17995]}    {[59]}    {0×0 double  }    {0×0 double}    {0×0 double   }

stats = struct with fields:
       gnames: [3×1 char]
            n: [20 20 20]
       source: 'kruskalwallis'
    meanranks: [26.7500 18.9500 45.8000]
         sumt: 0

p の戻り値は、有意水準 1% で帰無仮説を棄却することを示します。stats 構造体を使用して補足の検定を実行できます。cell 配列 tbl に、グラフィカルな ANOVA 表 (列と行のラベルを含む) と同じデータが含まれています。

別の分布から派生しているデータ標本を識別するための補足の検定を実行します。

c = multcompare(stats);

Note: Intervals can be used for testing but are not simultaneous confidence intervals.

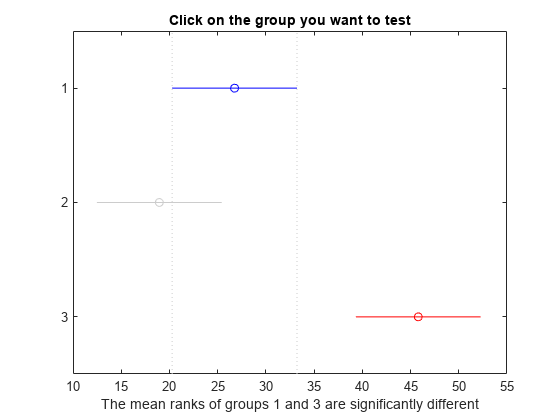
多重比較の結果を table で表示します。

tbl = array2table(c,"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"])

tbl=3×6 table
    Group A    Group B    Lower Limit     A-B      Upper Limit     P-value  
    _______    _______    ___________    ______    ___________    __________

       1          2         -5.1435         7.8       20.744         0.33446
       1          3         -31.994      -19.05      -6.1065       0.0016282
       2          3         -39.794      -26.85      -13.906      3.4768e-06

結果的に、グループ 1 とグループ 3 の間には有意差が認められたため、それらの 2 つのグループが同じ分布から派生しているという帰無仮説は棄却されます。同じことがグループ 2 および 3 についても成り立ちます。しかし、グループ 1 および 2 の間には有意な差がないので、この 2 つのグループが同じ分布に由来しているという帰無仮説は棄却されません。したがって、これらの結果から、グループ 1 とグループ 2 のデータが同じ分布から派生し、グループ 3 のデータは別の分布から派生していると考えられます。

グループ全体で同じ分布かどうか検定する

金属梁の強度の測定値を含む strength というベクトルと、対応する梁の原料である合金の種類を示す alloy というベクトルを作成します。

strength = [82 86 79 83 84 85 86 87 74 82 ...
            78 75 76 77 79 79 77 78 82 79];

alloy = {'st','st','st','st','st','st','st','st',...
         'al1','al1','al1','al1','al1','al1',...
         'al2','al2','al2','al2','al2','al2'};

梁の強度の測定値の分布が 3 つのいずれの金属合金でも同じになるという帰無仮説を検定します。

p = kruskalwallis(strength,alloy,'off')

p = 
0.0018

p の戻り値は、有意水準 1% で帰無仮説を棄却することを示します。

入力引数

x — 標本データ

ベクトル | 行列

仮説検定の標本データ。ベクトルまたは m 行 n 列の行列として指定します。x が m 行 n 列の行列の場合、n 個の各列が m 個の互いに独立した観測値を含む独立した標本を表します。

データ型: single | double

group — グループ化変数

数値ベクトル | logical ベクトル | 文字配列 | string 配列 | 文字ベクトルの cell 配列

グループ化変数。数値ベクトル、logical ベクトル、文字配列、string 配列、または文字ベクトルの cell 配列を指定します。

• x がベクトルの場合、group 内の各要素によって x 内で対応する要素の所属先グループが識別されるため、group は x と同じ長さのベクトルでなければなりません。group の行に空の値が含まれている場合、その行および x 内の対応する観測値は無視されます。x 内または group 内の NaN 値も同様に無視されます。

• x が行列の場合、x 内の各列は異なるグループを表します。group を使用して、それらの列のラベルを指定できます。group の要素数は x の列数と等しくなければなりません。

group に含まれるラベルは、箱ひげ図の注釈にも使用されます。

例: {'red','blue','green','blue','red','blue','green','green','red'}

データ型: single | double | logical | char | string | cell

displayopt — 表示オプション

'on' (既定値) | 'off'

表示オプション。'on' または 'off' として指定します。displayopt が 'on' の場合、kruskalwallis は次の図を表示します。

• ANOVA 表。この表には、二乗和、自由度、x のデータの順位に基づいて計算されたその他の数量が含まれます。

• データ行列 x の各列にあるデータの箱ひげ図。箱ひげ図は、ランクではなく、実際のデータ値に基づきます。

displayopt が 'off' の場合、kruskalwallis はこれらの図を表示しません。

displayopt の値を指定する場合は、group の値も指定しなければなりません。グループ化変数がない場合は、group を [] として指定します。

例: 'off'

出力引数

p — p 値

[0,1] の範囲のスカラー値

検定の p 値。[0,1] の範囲のスカラー値として返されます。p は、帰無仮説に基づく観測値と同様に、極端な検定統計量、またはより極端な検定統計量が観測される確率です。p の値が小さい場合、帰無仮説が有効でない可能性があります。

tbl — ANOVA 表

cell 配列

検定結果の ANOVA 表。cell 配列として返されます。tbl には、二乗和、自由度、x のデータの順位に基づいて計算されたその他の数量、列と行のラベルが含まれます。

stats — 検定データ

構造体

検定データ。構造体として返されます。stats を multcompare の入力値として使用して、標本中央値のペアに対する補足の多重比較検定を実行できます。

詳細

クラスカル・ワリス検定

クラスカル・ワリス検定は、従来型の 1 因子 ANOVA のノンパラメトリック バージョンであり、ウィルコクソン順位和検定を 3 つ以上のグループに拡張したものです。クラスカル・ワリス検定は、2 つ以上のグループがあるデータに対して有効です。x のデータのグループの中央値を比較して、標本が同じ母集団 (または同じ分布をもつ異なる母集団) から抽出されたものであるかを判定します。

クラスカル・ワリス検定では、検定統計量の計算にデータの数値ではなく順位を使用します。ランクは、データを最小値から最大値の順ですべてのグループにわたり並べ替えて、この順番の数値インデックスを取り出して算出します。関連づけられた観測のランクは、関連づけられているすべての観測の平均ランクに等しくなります。従来型の 1 因子 ANOVA で使用される F 統計量がカイ二乗統計量に置き換えられ、p 値でカイ二乗統計量の有意性を測定します。

クラスカル・ワリス検定は、グループの影響によって位置が異なる可能性はあるが、すべての標本が同じ連続分布をもつ母集団から取得されているという仮定と、すべての観測値が相互に独立しているという仮定に基づきます。それに対して、従来型の 1 因子 ANOVA では、母集団は正規分布をもつという強制力がより強い仮定で、最初の仮定が置き換えられます。

バージョン履歴

R2006a より前に導入

参考

anova1 | boxplot | friedman | multcompare | ranksum

トピック

• グループ化変数