friedman

フリードマン検定

構文

p = friedman(x,reps)

p = friedman(x,reps,displayopt)

[p,tbl] = friedman(___)

[p,tbl,stats] = friedman(___)

説明

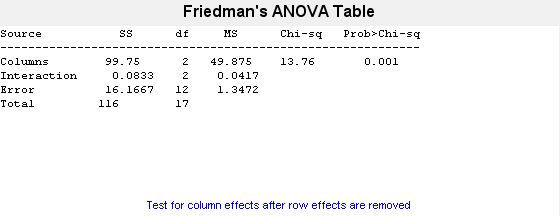
p = friedman(x,reps) はノンパラメトリックなフリードマン検定の p 値を返し、2 通りのレイアウトで列効果を比較します。friedman は、列効果がすべて等しいという帰無仮説を、必ずしも等しくはないという対立仮説に対して検定します。フリードマン検定は、交互作用がない 2 因子 ANOVA に似た解析を提供します。詳細については、フリードマン検定を参照してください。

p = friedman(x,reps,displayopt) は、displayopt が 'on' (既定値) の場合は表示、displayopt が 'off' の場合は非表示になる ANOVA 表の表示を有効にします。

[p,tbl] = friedman(___) は、cell 配列 tbl の ANOVA 表 (列と行のラベルを含む) を返します。

[p,tbl,stats] = friedman(___) も、補足の多重比較検定を実行するために使用できる stats 構造体を返します。

例

フリードマン検定を使用して列効果を検定する

この例では、フリードマン検定を使用して二元配置における列効果を検定する方法を示します。

標本データを読み込みます。

load popcorn
popcorn

popcorn = 6×3

    5.5000    4.5000    3.5000
    5.5000    4.5000    4.0000
    6.0000    4.0000    3.0000
    6.5000    5.0000    4.0000
    7.0000    5.5000    5.0000
    7.0000    5.0000    4.5000

これは、ポップコーンのブランドと製造器具タイプの研究 (Hogg 1987) のデータです。行列 popcorn の列はブランド (Gourmet、National、および Generic) を示しています。行は製造器具のタイプです (Oil と Air)。この研究では、それぞれの製造器具で、それぞれのブランドのポップコーンを 3 回ずつ作りました。値は、ポップコーンの生産量をカップ単位で示しています。

フリードマン検定を使用して、ポップコーンのブランドがポップコーンの生産量に影響するかどうかを判定します。

p = friedman(popcorn,3)

p = 
0.0010

p = 0.001 という小さい値は、ポップコーンのブランドがポップコーンの生産量に影響することを示します。

入力引数

x — 標本データ

行列

仮説検定の標本データ。行列として指定します。x の列は因子 A での変更を表します。行はブロッキング ファクター B での変更を表します。因子の組み合わせごとに複数の観測値が存在する場合、入力 reps は各 "セル" での反復数を示すため、定数でなければなりません。

データ型: single | double

reps — 反復数

1 (既定値) | 正の整数値

グループの各組み合わせについての反復数。正の整数値として指定します。たとえば、次のデータでは、行因子 A と列因子 B の各組み合わせについて 2 つの反復があります (reps = 2)。

$$\begin{array}{c}\begin{array}{cc}B=1& B=2\end{array}\\ \left[\begin{array}{cc}{x}_{111}& x_{121}\\ x_{112}& x_{122}\\ x_{211}& x_{221}\\ x_{212}& x_{222}\\ x_{311}& x_{321}\\ x_{312}& x_{322}\end{array}\right]\end{array}\begin{array}{c}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\}A=1\\ \begin{array}{c}\\ \end{array}\}A=2\\ \begin{array}{c}\\ \end{array}\}A=3\end{array}\end{array}$$

データ型: single | double

displayopt — ANOVA 表の表示オプション

'off' (既定値) | 'on'

ANOVA 表の表示オプション。'off' または 'on' として指定します。

displayopt が 'on' の場合、friedman は ANOVA 表を示す図を表示します。この表では、ランクの変動性が 2 つまたは 3 つの部分に分けられます。

• 列効果間の差違に起因する変化量

• 行と列の間の交互作用に起因する変動性 (reps が既定値 1 よりも大きい場合)

• 体系的な原因では説明できない残りのばらつき

ANOVA 表には、次の 6 つの列があります。

• 最初の列は変動性の原因を示します。

• 2 列目は、それぞれの要因の二乗和 (SS) を示します。

• 3 列目は、各原因に関連付けられた自由度 (df) を示します。

• 4 列目は平均二乗 (MS) で、これは比 SS/df です。

• 5 列目はフリードマンのカイ二乗統計量を示します。

• 6 列目はカイ二乗統計量の p 値を示します。

[編集] メニューから [テキストのコピー] を選択すると、ANOVA 表のテキスト バージョンをクリップボードにコピーできます。

出力引数

p — p 値

[0,1] の範囲のスカラー値

検定の p 値。[0,1] の範囲のスカラー値として返されます。p は、帰無仮説に基づく観測値と同様に極端な検定統計量、またはより極端な検定統計量が観測される確率です。p の値が小さい場合、帰無仮説の妥当性に問題がある可能性があります。

tbl — ANOVA 表

cell 配列

列および行ラベルを含む ANOVA 表。cell 配列として返されます。ANOVA 表には、次の 6 つの列があります。

• 最初の列は変動性の原因を示します。

• 2 列目は、それぞれの要因の二乗和 (SS) を示します。

• 3 列目は、各原因に関連付けられた自由度 (df) を示します。

• 4 列目は平均二乗 (MS) で、これは比 SS/df です。

• 5 列目はフリードマンのカイ二乗統計量を示します。

• 6 列目はカイ二乗統計量の p 値を示します。

[編集] メニューから [テキストのコピー] を選択すると、ANOVA 表のテキスト バージョンをクリップボードにコピーできます。

stats — 検定データ

構造体

検定データ。構造体として返されます。friedman は、列効果はすべて等しいという仮説を、必ずしも等しくはないという対立仮説に対して評価します。しかし、どの列効果のペアに有意差があり、どの列効果のペアについてはそうでないかを確認する検定を実行した方が良い場合もあります。関数 multcompare を使用して、stats を入力値として指定することでこのような検定を実行できます。

詳細

フリードマン検定

フリードマン検定は従来型の平衡 2 因子 ANOVA に類似していますが、フリードマン検定では、行効果として可能なものについて調整した後で、列効果に対してのみ検定が行われます。行効果や交互作用の効果については検定されません。フリードマン検定が利用されるのは、列が研究中の処理を表し、行が考慮する必要がありながらも関心のもたれない障害となる効果 (ブロック) を表すときです。

X の異なる列は因子 A の変化を表します。異なる行はブロック因子 B の変化を表します。因子の各組み合わせに対して複数の観測値がある場合、入力引数 reps では各 "セル" の反復数を指定します。これは定数でなければなりません。

以下の行列は、列因子 A に 3 つの水準があり、行因子 B に 2 つの水準があり、反復が 2 回ある (reps=2) 設定の形式を示しています。添字はそれぞれ、行、列、および反復を示しています。

$$\left[\begin{array}{ccc}{x}_{111}& x_{121}& x_{131}\\ x_{112}& x_{122}& x_{132}\\ x_{211}& x_{221}& x_{231}\\ x_{212}& x_{222}& x_{232}\end{array}\right]$$

フリードマン検定では以下の型のモデルが想定されます。

$$x_{ijk}=\mu +{\alpha }_i+{\beta }_j+{\epsilon }_{ijk}$$

ここで、μは全体の位置パラメーター、$${\alpha }_i$$ は列効果、$${\beta }_j$$ は行効果、$${\epsilon }_{ijk}$$ は誤差を表します。この検定では B の各水準内にあるデータが順位付けされ、A の全水準における差違に対して検定が行われます。friedman が返す p は、$${\alpha }_i=0$$ という帰無仮説に対する p 値です。p 値がゼロに近いと、帰無仮説の信ぴょう性が疑われます。p 値がかなり小さいのは、少なくとも 1 つの列標本中央値がその他の中央値と比べて著しく異なることを示しています。つまり、因子 A に起因する主効果があります。結果が "統計的に有意" かどうかを判定するための棄却限界値 p の選択は、解析する人に委ねられます。p 値が 0.05 または 0.01 未満の場合、一般的に有意義な結果であると言えます。

フリードマン検定では、X 内のデータについて次のように仮定します。

• すべてのデータは、列効果と行効果を起因として場合によっては位置が異なる点を除けば、同一の連続分布を有する母集団から派生していること。

• すべての観測が互いに独立していること。

従来型の 2 因子 ANOVA では、データは正規分布から派生するという、より強力な仮定によって最初の仮定が置き換えられます。

参照

[1] Hogg, R. V., and J. Ledolter. Engineering Statistics. New York: MacMillan, 1987.

[2] Hollander, M., and D. A. Wolfe. Nonparametric Statistical Methods. Hoboken, NJ: John Wiley & Sons, Inc., 1999.

バージョン履歴

R2006a より前に導入

参考

anova2 | multcompare | kruskalwallis