multcompare

多重比較検定

ページ内をすべて折りたたむ

構文

c = multcompare(stats)

c = multcompare(stats,Name,Value)

[c,m] = multcompare(___)

[c,m,h] = multcompare(___)

[c,m,h,gnames] = multcompare(___)

説明

例

c = multcompare(stats) は、stats 構造体に保存された情報を使用して多重比較検定のペアを比較した結果の行列 c を返します。また、multcompare も推定および比較区間の対話型グラフを表示します。各グループの平均はシンボルで表示されます。また、区間はシンボルからの線により表示されます。区間が重なっていない場合は 2 つグループの平均には有意差があり、区間が重なっている場合は有意差はありません。マウスを使用して任意のグループ選択する場合、有意差があれば、グラフは有意差のあるその他すべてのグループを強調表示します。

例

c = multcompare(stats,Name,Value) では、1 つ以上の名前と値の引数を使用してオプションを指定します。たとえば、信頼区間または多重比較検定で使用する棄却限界値の種類を指定できます。

[c,m] = multcompare(___) が返す行列 m には、グループごとの平均の推定値 (または比較対象の統計量) および対応する標準誤差が含まれます。前述の構文のいずれも使用できます。

[c,m,h] = multcompare(___) は、比較グラフのハンドル h も返します。

例

[c,m,h,gnames] = multcompare(___) は、グループ名が含まれる cell 配列 gnames も返します。

例

すべて折りたたむ

グループ平均の多重比較

ライブスクリプトを開く

carsmall データセットを読み込みます。

load carsmall

データには、さまざまな車種およびモデルのガロンあたりの走行マイル数 (MPG) の測定値が格納され、生産国 (Origin) およびその他の車両の特性によってグループ化されています。

1 因子分散分析 (ANOVA) を実行し、自動車の MPG 値が生産国によって異なるかどうかを確認します。

[p,t,stats] = anova1(MPG,Origin);

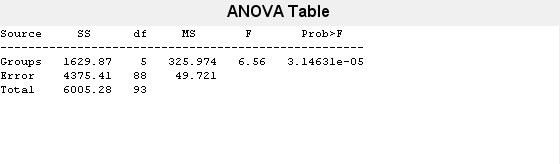
Figure One-way ANOVA contains objects of type uicontrol.

Figure contains an axes object. The axes object contains 42 objects of type line.

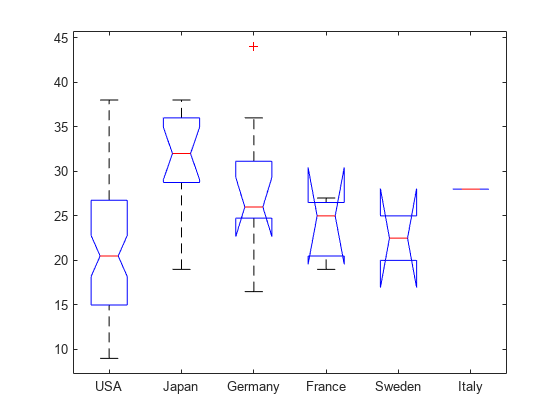
"p" 値 (列 Prob>F の値) が小さいので、グループ平均には有意な違いがあることがわかります。ただし、どのグループが異なる平均値をもつかは ANOVA の結果からはわかりません。多重比較検定を使用して一対比較を実行すると、有意に異なる平均値をもつグループを特定できます。

グループ平均の多重比較検定を実行します。

[c,m,h,gnames] = multcompare(stats);

Figure Multiple comparison of means contains an axes object. The axes object with title Click on the group you want to test contains 13 objects of type line.

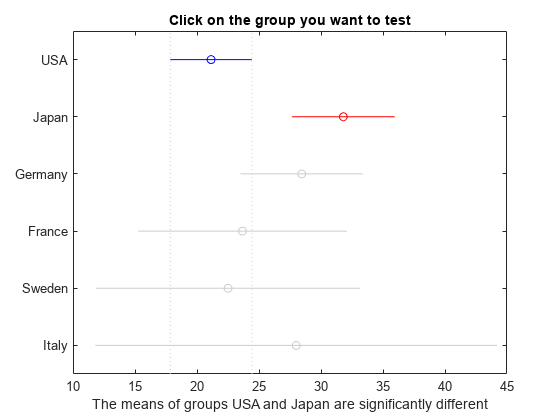
multcompare は推定値とその周辺の比較間隔を表示します。任意の国のグラフをクリックすると、その国の平均を他の国の平均と比較できます。

平均の推定値、標準誤差、および該当するグループ名を table で表示します。

tbl = array2table(m,"RowNames",gnames, ...
    "VariableNames",["Mean","Standard Error"])

tbl=6×2 table
                Mean     Standard Error
               ______    ______________

    USA        21.133       0.88141    
    Japan        31.8        1.8206    
    Germany    28.444        2.3504    
    France     23.667        4.0711    
    Sweden       22.5         4.986    
    Italy          28        7.0513

制御グループとの多重比較

ライブスクリプトを開く

ダネットの検定を使用して制御グループに対して多重比較検定を実行し、その結果をテューキーの HSD 法による一対比較の結果と比較します。

carsmall データセットを読み込みます。

load carsmall

1 因子 ANOVA を実行し、生産国によって定義されたグループ間で自動車の燃費を比較します。

[~,~,stats] = anova1(MPG,Origin,"off");

グループの名前を表示します。

stats.gnames

ans = 6x1 cell
    {'USA'    }
    {'Japan'  }
    {'Germany'}
    {'France' }
    {'Sweden' }
    {'Italy'  }

グループ平均の多重比較の例に示したグループのすべての異なるペアに関する多重比較の結果によると、米国と日本の平均値が有意に異なります。この例では、既定の検定であるテューキーの HSD 法を使用しています。

ダネットの検定を使用して、グループ平均を制御グループと比較します。

CriticalValueTypeを "dunnett" と指定して、ダネットの検定を実行します。既定では、multcompare は最初のグループ (米国) を制御グループとして選択します。名前と値の引数ControlGroupを使用して、異なる制御グループを選択できます。

[results,~,~,gnames] = multcompare(stats,"CriticalValueType","dunnett");

Figure Multiple comparison of means contains an axes object. The axes object contains 13 objects of type line.

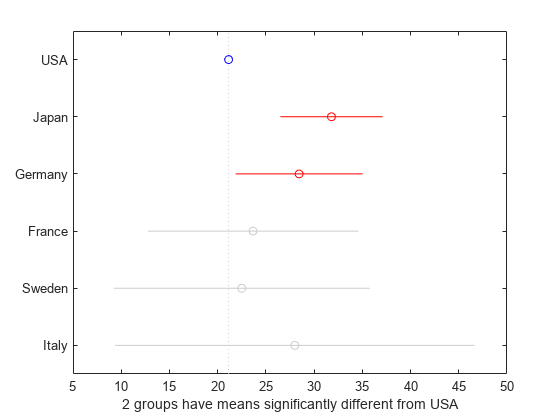
図の青い円は、制御グループの平均を示しています。赤い円とバーは、制御グループの平均と有意に異なる平均値をもつグループの平均値および信頼区間を表しています。赤いバーは、制御グループの平均を表す垂直方向の点線と交差していないことに注意してください。有意に異なる平均値をもたないグループはグレーで表示されています。

ダネットの検定により、日本とドイツの 2 つのグループが米国 (制御グループ) の平均と有意に異なる平均値をもつことがわかります。グループ平均の多重比較の例で、既定の方法 (テューキーの HSD 法) ではドイツが特定されなかったことに注意してください。結果の差異は、2 つの比較検定の保守度が異なることに関連しています。ダネットの検定は制御グループとの比較のみを考慮するため、既定の方法ほど保守的ではありません。既定の方法では、グループのすべての異なるペアについて一対比較を実行します。

多重比較の結果と該当するグループ名を table で表示します。

tbl = array2table(results,"VariableNames", ...
    ["Group","Control Group","Lower Limit","Difference","Upper Limit","P-value"]);
tbl.("Group") = gnames(tbl.("Group"));
tbl.("Control Group") = gnames(tbl.("Control Group"))

tbl=5×6 table
       Group       Control Group    Lower Limit    Difference    Upper Limit     P-value 
    ___________    _____________    ___________    __________    ___________    _________

    {'Japan'  }       {'USA'}          5.3649        10.667        15.969       4.727e-06
    {'Germany'}       {'USA'}         0.73151        7.3116        13.892        0.022346
    {'France' }       {'USA'}         -8.3848        2.5339        13.453         0.97912
    {'Sweden' }       {'USA'}         -11.905        1.3672         14.64         0.99953
    {'Italy'  }       {'USA'}          -11.76        6.8672        25.495         0.86579

2 因子 ANOVA の多重比較

ライブスクリプトを開く

標本データを読み込みます。

load popcorn
popcorn

popcorn = 6×3

    5.5000    4.5000    3.5000
    5.5000    4.5000    4.0000
    6.0000    4.0000    3.0000
    6.5000    5.0000    4.0000
    7.0000    5.5000    5.0000
    7.0000    5.0000    4.5000

このデータは、ポップコーンのブランドと製造器具タイプに関する研究 (Hogg 1987) によるものです。行列 popcorn の列はブランド (Gourmet、National、および Generic) を示しています。行は製造器具のタイプ (オイルとエアー) です。初めの 3 行はオイルタイプの製造器具、最後の 3 行はエアータイプの製造器具に対応しています。この研究では、各製造器具で各ブランドのポップコーンを 3 回ずつ作りました。値は、ポップコーンの生産量をカップ単位で示しています。

2 因子 ANOVA を実行します。主効果について多重比較検定を実行するために必要な統計量も計算します。

[~,~,stats] = anova2(popcorn,3,"off")

stats = struct with fields:
      source: 'anova2'
     sigmasq: 0.1389
    colmeans: [6.2500 4.7500 4]
        coln: 6
    rowmeans: [4.5000 5.5000]
        rown: 9
       inter: 1
        pval: 0.7462
          df: 12

構造体 stats には次の情報が含まれています。

平均二乗誤差 (sigmasq)
各ポップコーンブランドの平均生産量の推定値 (colmeans)
各ポップコーンブランドの観測数 (coln)
各製造器具タイプの平均生産量の推定値 (rowmeans)
各製造器具タイプの観測数 (rown)
交互作用の数 (inter)
交互作用項の有意水準を示す p 値 (pval)
誤差自由度 (df)

多重比較検定を実行して、出来上がるポップコーンの量がポップコーンブランド (列) のペア間で異なるかどうかを調べます。

c1 = multcompare(stats);

Note: Your model includes an interaction term.  A test of main effects can be 
difficult to interpret when the model includes interactions.

Figure Multiple comparison of column means contains an axes object. The axes object with title Click on the group you want to test contains 7 objects of type line.

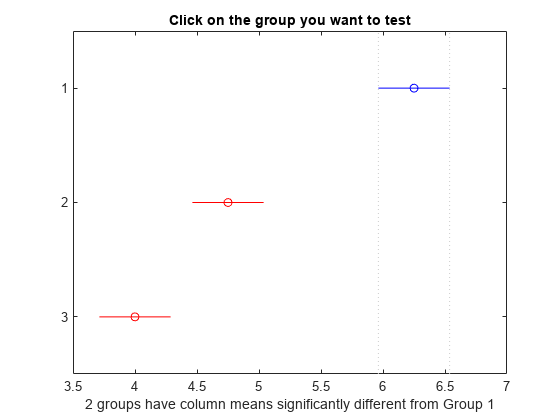
図には、平均の多重比較が示されています。既定では、グループ 1 の平均が強調表示され、比較区間が青になります。他の 2 つのグループの比較区間は、グループ 1 の平均の区間と重なっていないので、赤で強調表示されています。区間が重なっていないことから、どちらの平均もグループ 1 の平均と異なることがわかります。他のグループの平均を選択して、すべてのグループの平均が他と有意に異なることを確認します。

多重比較の結果を table で表示します。

tbl1 = array2table(c1,"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"])

tbl1=3×6 table
    Group A    Group B    Lower Limit    A-B     Upper Limit     P-value  
    _______    _______    ___________    ____    ___________    __________

       1          2         0.92597       1.5       2.074       4.1188e-05
       1          3           1.676      2.25       2.824       6.1588e-07
       2          3         0.17597      0.75       1.324         0.011591

c1 の初めの 2 列には、比較したグループが示されています。4 列目には、推定したグループ平均の間の差が示されています。3 列目と 5 列目には、真の平均の差に関する 95% 信頼区間の下限と上限が示されています。6 列目には、対応する平均の差がゼロに等しいという仮説を検定するための p 値が含まれています。すべての "p" 値が非常に小さいので、3 つのブランドすべてででき上がるポップコーンの量が異なることがわかります。

多重比較検定を実行して、出来上がるポップコーンの量が 2 種類の製造器具タイプ (行) の間で異なるかどうかを調べます。

c2 = multcompare(stats,"Estimate","row");

Note: Your model includes an interaction term.  A test of main effects can be 
difficult to interpret when the model includes interactions.

Figure Multiple comparison of row means contains an axes object. The axes object with title Click on the group you want to test contains 5 objects of type line.

tbl2 = array2table(c2,"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"])

tbl2=1×6 table
    Group A    Group B    Lower Limit    A-B    Upper Limit     P-value  
    _______    _______    ___________    ___    ___________    __________

       1          2         -1.3828      -1      -0.61722      0.00010037

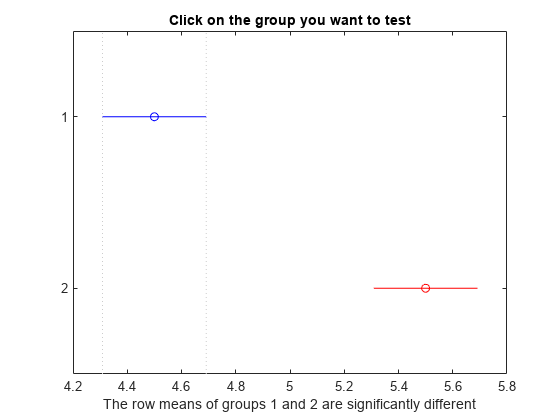
"p" 値が小さいので、でき上がるポップコーンの量は 2 つの製造器具タイプ (エアーとオイル) で異なることがわかります。図には同じ結果が示されています。比較区間が重なっていないので、グループの平均が互いに有意に異なることがわかります。

3 因子 ANOVA の多重比較

ライブスクリプトを開く

標本データを読み込みます。

y = [52.7 57.5 45.9 44.5 53.0 57.0 45.9 44.0]';
g1 = [1 2 1 2 1 2 1 2];
g2 = ["hi" "hi" "lo" "lo" "hi" "hi" "lo" "lo"];
g3 = ["may" "may" "may" "may" "june" "june" "june" "june"];

y は応答ベクトル、g1、g2 および g3 はグループ化変数 (因子) です。各因子には 2 つのレベルがあり、y のすべての観測値は因子のレベルの組み合わせによって識別されます。たとえば、観測値 y(1) は、因子 g1 のレベル 1、因子 g2 のレベル hi および因子 g3 のレベル may に関連付けられています。同様に、観測値 y(6) は、因子 g1 のレベル 2、因子 g2 のレベル hi および因子 g3 のレベル june に関連付けられています。

すべての因子レベルについて応答が同じであるか検定します。また、多重比較検定に必要な統計量も計算します。

[~,~,stats] = anovan(y,{g1 g2 g3},"Model","interaction", ...
    "Varnames",["g1","g2","g3"]);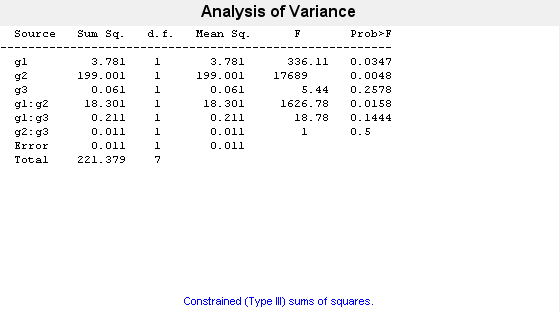

Figure N-Way ANOVA contains objects of type uicontrol.

0.2578 という "p" 値は、因子 g3 のレベル may および june について平均応答が有意には異なっていないことを示しています。0.0347 という p 値は、因子 g1 のレベル 1 および 2 について平均応答が有意に異なっていることを示しています。同様に、0.0048 という "p" 値は、因子 g2 のレベル hi および lo について平均応答が有意に異なっていることを示しています。

多重比較検定を実行し、因子 g1 および g2 についてどのグループが有意に異なるかを調べます。

[results,~,~,gnames] = multcompare(stats,"Dimension",[1 2]);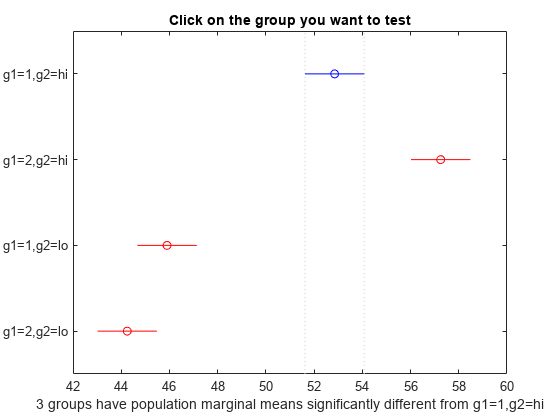

Figure Multiple comparison of population marginal means contains an axes object. The axes object with title Click on the group you want to test contains 9 objects of type line.

対応するグループの比較区間をクリックすると、他のグループについて検定を行うことができます。クリックしたバーは青になります。有意に異なるグループのバーは、赤になります。有意には異ならないグループのバーは、灰色になります。たとえば、g1 のレベル 1 と g2 のレベル lo の組み合わせの比較区間をクリックすると、g1 のレベル 2 と g2 のレベル lo の組み合わせの比較区間は重なるので灰色になります。逆に、他の比較区間は赤になり、有意に異なることを示します。

多重比較の結果と該当するグループ名を table で表示します。

tbl = array2table(results,"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"]);
tbl.("Group A")=gnames(tbl.("Group A"));
tbl.("Group B")=gnames(tbl.("Group B"))

tbl=6×6 table
       Group A           Group B        Lower Limit     A-B     Upper Limit     P-value 
    ______________    ______________    ___________    _____    ___________    _________

    {'g1=1,g2=hi'}    {'g1=2,g2=hi'}      -6.8604       -4.4      -1.9396       0.027249
    {'g1=1,g2=hi'}    {'g1=1,g2=lo'}       4.4896       6.95       9.4104       0.016983
    {'g1=1,g2=hi'}    {'g1=2,g2=lo'}       6.1396        8.6        11.06       0.013586
    {'g1=2,g2=hi'}    {'g1=1,g2=lo'}       8.8896      11.35        13.81       0.010114
    {'g1=2,g2=hi'}    {'g1=2,g2=lo'}        10.54         13        15.46      0.0087375
    {'g1=1,g2=lo'}    {'g1=2,g2=lo'}      -0.8104       1.65       4.1104        0.07375

関数 multcompare は、2 つのグループ化変数 g1 および g2 についてグループ (レベル) の組み合わせを比較します。たとえば、この行列の 1 行目は、g1 のレベル 1 と g2 のレベル hi の組み合わせが g1 のレベル 2 と g2 のレベル hi の組み合わせと同じ平均応答値になっていることを示しています。この検定に対応する "p" 値は 0.0272 なので、平均応答が有意に異なっていることがわかります。この結果は、図からもわかります。青いバーは、g1 のレベル 1 と g2 のレベル hi の組み合わせについて平均応答の比較区間を示しています。赤いバーは、他のグループの組み合わせについて平均応答の比較区間を示しています。どの赤いバーも青いバーと重なっていないので、g1 のレベル 1 と g2 のレベル hi の組み合わせの平均応答が他のグループの組み合わせの平均応答と有意に異なっていることがわかります。

入力引数

すべて折りたたむ

`stats` — 検定データ
構造体

検定データ。構造体として指定します。以下の関数のいずれかを使用して構造体を作成できます。

anova1 — 1 因子分散分析
anova2 — 2 因子分散分析
anovan — N 因子分散分析
aoctool — 対話型共分散分析ツール
friedman — フリードマン検定
kruskalwallis — クラスカル・ワリス検定

multcompare は、変量効果または入れ子形式の効果を含むモデルに anovan 出力を使用する多重比較をサポートしません。変量効果モデルでの計算は、すべての効果が固定として処理される警告を生成します。入れ子形式のモデルは受け入れません。

データ型: struct

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

例: Alpha=0.01,CriticalValueType="bonferroni",Display="off" はボンフェローニの棄却限界値を計算し、1% の有意水準で仮説検定を行い、対話型表示を行いません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: "Alpha",0.01,"CriticalValueType","bonferroni","Display","off"

`Alpha` — 有意水準
`0.05` (既定値) | (0,1) の範囲のスカラー値

多重比較検定の有意水準。(0,1) の範囲のスカラー値として指定します。Alpha について指定された値は、行列 c に返された区間および Figure における区間に対する 100 × (1 – α)% の信頼度を決定します。

例: "Alpha",0.01

データ型: single | double

`Approximate` — 近似法を使用してダネットの検定用の棄却限界値を計算するためのフラグ
`true` または `1` | `false` または `0`

近似法を使用してダネットの検定用の棄却限界値を計算するためのフラグ。logical 1 (true) または 0 (false) として指定します。

関数 multcompare は、多変量 t 分布を積分してダネットの検定用の棄却限界値を求めます。多因子 (n 因子) ANOVA では、n が大きい場合は計算速度が低下する可能性があります。計算を高速化するには、Approximate を true に指定して近似法 ([5]) を使用します。近似法にはランダム性があります。結果を再現する場合は、multcompare を呼び出す前に関数 rng を使用して乱数シードを設定します。

stats のソースが anovan である場合、既定値は true です。それ以外の場合、既定値は false です。

この引数は、CriticalValueType が "dunnett" である場合のみ有効です。

例: "Approximate",true

データ型: logical

`ControlGroup` — ダネットの検定に使用する制御グループのインデックス
`1` (既定値) | 正の整数値

ダネットの検定に使用する制御グループのインデックス。正の整数値として指定します。

関数 multcompare で比較するグループのいずれかを制御グループとして指定します。ControlGroup を idx と指定すると仮定します。次の表に、stats のソースによって異なる制御グループ値を示します。

`stats` のソース	制御グループ
`anova1`	`multcompare` は、`stats.means(idx)` に対応するグループ `stats.gnames(idx)` を制御グループとして使用します。
`anova2`	`multcompare` は、`stats.colmeans(idx)` (`Estimate` が `"column"` の場合 (既定)) または `stats.rowmeans(idx)` (`Estimate` が `"row"` の場合) に対応するグループを制御グループとして使用します。
`anovan`	`Dimension` を `d` と指定する場合、`multcompare` は `stats.grpnames{d}(idx)` を制御グループとして使用します。
`aoctool`	`multcompare` は、`stats.gnames(idx)` を制御グループとして使用します。
`friedman`	`multcompare` は、`stats.meanranks(idx)` に対応するグループを制御グループとして使用します。
`kruskalwallis`	`multcompare` は、`stats.meanranks(idx)` に対応するグループ `stats.gnames(idx)` を制御グループとして使用します。

この引数は、CriticalValueType が "dunnett" である場合のみ有効です。

例: "ControlGroup",3

データ型: single | double

`CriticalValueType` — 棄却限界値の種類
`"tukey-kramer"` (既定値) | `"lsd"` | `"dunnett"` | `"dunn-sidak"` | `"bonferroni"` | `"scheffe"`

多重比較検定に使用する棄却限界値の種類。次のいずれかを指定します。

値	説明
`"lsd"`	フィッシャーの最小有意差法
`"dunnett"`	ダネットの検定
`"tukey-kramer"` または `"hsd"` (既定の設定)	テューキーの HSD 法
`"dunn-sidak"`	ダンとシダックのアプローチ
`"bonferroni"`	ボンフェローニの方法
`"scheffe"`	シェッフェの方法

この表は、棄却限界値の種類を保守度が低いものから順に並べた一覧です。検定ごとに多重比較の問題の防止レベルが異なります。

"lsd" では保護は提供されません。
"dunnett" では、制御グループとの比較について保護が提供されます。
"tukey-kramer"、"dunn-sidak"、および "bonferroni" では、一対比較について保護が提供されます。
"scheffe" では、一対比較と推定値のすべての線形結合の比較について保護が提供されます。

詳細については、多重比較法を参照してください。

例: "CriticalValueType","bonferroni"

データ型: string | char

`Display` — 表示切り替え
`"on"` (既定値) | `"off"`

表示切り替え。"on" または "off" として指定します。"on" を指定する場合、multcompare は推定値のグラフおよびその比較区間を表示します。"off" を指定する場合、multcompare はグラフの表示を省略します。

例: "Display","off"

データ型: string | char

`Dimension` — 周辺平均を計算する次元
`1` (既定値) | 正の整数値 | 正の整数値のベクトル

母集団周辺平均を計算する次元。正の整数値またはそのような値のベクトルとして指定します。CriticalValueType を "dunnett" と指定する場合、次元は 1 つのみ指定できます。

この引数は、関数 anovan を使用して入力構造体 stats を作成する場合のみ有効です。

たとえば、Dimension を 1 と指定する場合、multcompare は第 1 グループ化変数の各値の平均を比較し、他のグループ化変数の効果を除去することで、設計が平衡化されているかのように調整します。Dimension を [1,3] と指定する場合、multcompare は、第 1 および第 3 のグループ化変数のそれぞれの組み合わせに対応する母集団周辺平均を計算しますが、第 2 のグループ化変数の効果を除去します。特異なモデルを近似する場合、一部のセルの平均は推定できない場合があり、その場合、これらのセル平均に依存する母集団周辺平均はすべて、値 NaN をもちます。

母集団周辺平均については、Milliken, Johnson (1992)、および、Searle, Speed, Milliken (1980) によって述べられています。母集団周辺平均の背景となるアイデアは、Dimension で指定される因子の値を固定し、各因子の組み合わせが同じ回数起こるかのように、他の因子の効果を平均化することにより、不平衡な設計の影響をすべて除くことです。母集団周辺平均の定義は、各因子の組み合わせでの観測の数に依存していません。各因子の組み合わせでの観測の数が意味をもたないように設定されている実験では、母集団周辺平均は、他の因子を無視した単純な平均よりも解釈が容易である可能性があります。因子の各組み合わせでの観測数が意味をもつ調査や研究では、母集団周辺平均は解釈が難しい場合があります。

例: "Dimension",[1,3]

データ型: single | double

`Estimate` — 比較する推定
`"column"` (既定値) | `"row"` | `"slope"` | `"intercept"` | `"pmm"`

比較する推定。許容値として指定します。Estimate の許容値は入力構造体 stats の生成に使用する関数により異なり、以下の表に従います。

関数	値
`anova1`	なし。`multcompare` はこの引数を無視し、グループ平均を常に比較します。
`anova2`	列平均を比較する `"column"` または行平均を比較する `"row"` のいずれか。
`anovan`	なし。`multcompare` はこの引数を無視し、名前と値の引数 `Dimension` で指定された母集団周辺平均を常に比較します。
`aoctool`	傾き、切片または母集団周辺平均をそれぞれ比較するために、`"slope"`、`"intercept"`、`"pmm"` のいずれかを使用します。共分散モデルの解析が別個の傾きを含まなければ、`"slope"` は使用できません。モデルが別個の切片を含まなければ、比較はできません。
`friedman`	なし。`multcompare` はこの引数を無視し、列のランクの平均を常に比較します。
`kruskalwallis`	なし。`multcompare` はこの引数を無視し、グループランクの平均を常に比較します。

例: "Estimate","row"

データ型: string | char

出力引数

すべて折りたたむ

`c` — 多重比較の結果の行列
スカラー値の行列

多重比較の結果の行列。p 行 6 列のスカラー値の行列として返します。ここで p はグループのペア数です。行列の各行には、1 組の比較検定の結果が含まれます。列 1 および 2 には、比較する 2 つの標本のインデックスが含まれます。列 3 には、信頼区間の下限が含まれ、列 4 には推定が含まれます。列 5 には信頼区間の上限が含まれます。列 6 には、対応する平均との差が 0 ではないことを仮説検定する p 値が含まれます。

たとえば、1 つの行が次の要素を含むとします。

2.0000  5.0000  1.9442  8.2206  14.4971 0.0432

これらの数値は、グループ 2 の平均からグループ 5 の平均を引くと、8.2206 と推定され、真の差の平均に対する 95% の信頼区間は、[1.9442, 14.4971] であることを示しています。グループ 2 とグループ 5 の平均の差が 0 から大きく離れているという仮説検定の p 値は 0.0432 です。

この例では、信頼区間は 0 を含みません。したがって、差は 5% の有意水準で有意になります。信頼区間が 0 を含む場合、差は有意ではありません。p 値 0.0432 も、グループ 2 とグループ 5 の平均の差が 0 から大きく離れていることを示しています。

`m` — 推定の行列
スカラー値の行列

推定の行列。スカラー値の行列として返します。m の 1 列目は、各グループの平均の推定値 (または、比較対象の統計量) を含みます。そして、2 列目は、それらの標準誤差を含みます。

`h` — Figure のハンドル
ハンドル

対話型グラフを含む Figure のハンドル。ハンドルとして返します。このグラフのタイトルは、グラフとの対話に関する命令を含み、x 軸ラベルは、選択される平均と比べてどの平均に有意差があるかについての情報を含みます。このグラフをプレゼンテーションに使用する場合、タイトルと x 軸ラベルを省略することをお勧めします。グラフウィンドウの対話型機能を使用するか、次のコマンドを使用すると、それらを除去できます。

title("")
xlabel("")

`gnames` — グループ名
文字ベクトルの cell 配列

グループ名。文字ベクトルの cell 配列として返されます。gnames の各行にはグループ名が含まれます。

詳細

すべて折りたたむ

多重比較検定

分散分析では複数のグループの平均を比較して、グループの平均が必ずしも等しくないという一般的な対立仮説に対して、すべてが等しいという仮説を検定します。この対立仮説では、一般的すぎる場合もあります。平均のどのペアに有意差があり、どのペアがそうでないかに関しての情報が必要となることもあります。多重比較検定 はこの情報を提供できます。

他のグループに対して 1 つのグループの平均に関する単純な t 検定を実行するとき、t 統計量のカットオフの値を決定する有意水準を指定します。たとえば、実際の差がない場合に有意差を誤って求める確率を 5% 以下にするには、alpha = 0.05 という値を指定します。多数のグループ平均がある場合、比較するペアも多くなります。この状況で、通常の t 検定を適用する場合、alpha の値は各比較に適用されるため、有意差を誤って見つけるという可能性は、比較の数の増加と共に増えます。多重比較のアルゴリズムは、"任意の" 比較を誤って有意であるとしてしまう確率に、上界を与えるように設定されます。

帰無仮説と対立仮説

関数 multcompare は、名前と値の引数 CriticalValueType で指定された棄却限界値の種類に応じて異なるセットの帰無仮説 (H₀) と対立仮説 (H₁) を調べます。

ダネットの検定 (CriticalValueType が "dunnett") では、制御グループとの多重比較を実行します。そのため、制御グループとの比較に関する帰無仮説と対立仮説は次のようになります。

$\begin{array}{l} H_{0} : m_{i} = m_{0}, \\ H_{1} : m_{i} \neq m_{0}, \end{array}$
ここで、m_i と m₀ はそれぞれグループ i と制御グループの推定値です。この関数は、制御グループ以外のすべてのグループについて H₀ と H₁ を複数回調べます。
その他の検定では、multcompare はグループのすべての異なるペアについて多重対比較を実行します。グループ i とグループ j の一対比較の帰無仮説と対立仮説は次のようになります。

$\begin{matrix} H_{0} : m_{i} = m_{j}, \\ H_{1} : m_{i} \neq m_{j} . \end{matrix}$

参照

[1] Hochberg, Y., and A. C. Tamhane. Multiple Comparison Procedures. Hoboken, NJ: John Wiley & Sons, 1987.

[2] Milliken, G. A., and D. E. Johnson. Analysis of Messy Data, Volume I: Designed Experiments. Boca Raton, FL: Chapman & Hall/CRC Press, 1992.

[3] Searle, S. R., F. M. Speed, and G. A. Milliken. “Population marginal means in the linear model: an alternative to least-squares means.” American Statistician. 1980, pp. 216–221.

[4] Dunnett, Charles W. “A Multiple Comparison Procedure for Comparing Several Treatments with a Control.” Journal of the American Statistical Association, vol. 50, no. 272, Dec. 1955, pp. 1096–121.

[5] Krishnaiah, Paruchuri R., and J. V. Armitage. "Tables for multivariate t distribution." Sankhyā: The Indian Journal of Statistics, Series B (1966): 31-56.

バージョン履歴

R2006a より前に導入

すべて展開する

R2022a: `CType` の名前を `CriticalValueType` に変更

名前と値の引数 CType は、その機能をわかりやすくするために名前が CriticalValueType に変更されました。

参考

トピック

多重比較

multcompare

構文

説明

例

グループ平均の多重比較

制御グループとの多重比較

2 因子 ANOVA の多重比較

3 因子 ANOVA の多重比較

入力引数

stats — 検定データ 構造体

名前と値の引数

Alpha — 有意水準 0.05 (既定値) | (0,1) の範囲のスカラー値

Approximate — 近似法を使用してダネットの検定用の棄却限界値を計算するためのフラグ true または 1 | false または 0

ControlGroup — ダネットの検定に使用する制御グループのインデックス 1 (既定値) | 正の整数値

CriticalValueType — 棄却限界値の種類 "tukey-kramer" (既定値) | "lsd" | "dunnett" | "dunn-sidak" | "bonferroni" | "scheffe"

Display — 表示切り替え "on" (既定値) | "off"

Dimension — 周辺平均を計算する次元 1 (既定値) | 正の整数値 | 正の整数値のベクトル

Estimate — 比較する推定 "column" (既定値) | "row" | "slope" | "intercept" | "pmm"

出力引数

c — 多重比較の結果の行列 スカラー値の行列

m — 推定の行列 スカラー値の行列

h — Figure のハンドル ハンドル

gnames — グループ名 文字ベクトルの cell 配列

詳細

多重比較検定

帰無仮説と対立仮説

参照

バージョン履歴

R2022a: CType の名前を CriticalValueType に変更

参考

トピック

`stats` — 検定データ
構造体

`Alpha` — 有意水準
`0.05` (既定値) | (0,1) の範囲のスカラー値

`Approximate` — 近似法を使用してダネットの検定用の棄却限界値を計算するためのフラグ
`true` または `1` | `false` または `0`

`ControlGroup` — ダネットの検定に使用する制御グループのインデックス
`1` (既定値) | 正の整数値

`CriticalValueType` — 棄却限界値の種類
`"tukey-kramer"` (既定値) | `"lsd"` | `"dunnett"` | `"dunn-sidak"` | `"bonferroni"` | `"scheffe"`

`Display` — 表示切り替え
`"on"` (既定値) | `"off"`

`Dimension` — 周辺平均を計算する次元
`1` (既定値) | 正の整数値 | 正の整数値のベクトル

`Estimate` — 比較する推定
`"column"` (既定値) | `"row"` | `"slope"` | `"intercept"` | `"pmm"`

`c` — 多重比較の結果の行列
スカラー値の行列

`m` — 推定の行列
スカラー値の行列

`h` — Figure のハンドル
ハンドル

`gnames` — グループ名
文字ベクトルの cell 配列

R2022a: `CType` の名前を `CriticalValueType` に変更