多重比較

分散分析 (ANOVA) 手法では、一連のグループの平均 (処理効果) が等しいかどうかを検定します。帰無仮説が棄却された場合、すべてのグループの平均が等しいわけではないという結論が得られます。しかし、この結果からはどのグループの平均が異なるかに関する詳しい情報は得られません。

どの平均のペアが有意に異なるかを判別するために一連の t 検定を実行することは推奨されません。複数の t 検定を実行した場合、平均が有意であると考えられる確率と有意差の結果は、多数の検定を行ったことが原因かもしれません。これらの t 検定は、同じ標本のデータを使用するので、独立していません。このため、複数の検定の有意水準を定量化することがより困難になります。

実際には真である帰無仮説 (H₀) が 1 回の t 検定で棄却される確率が小さい値 (たとえば 0.05) であるとします。そして、独立した t 検定を 6 回行ったとします。各検定の有意水準が 0.05 の場合、H₀ が各ケースについて真であるとすると、H₀ が検定により棄却できないという正しい結果になる確率は (0.95)⁶ = 0.735 です。そして、いずれかの検定により帰無仮説が誤って棄却される確率は 1 - 0.735 = 0.265 になります。これは、0.05 よりはるかに大きい値です。

複数検定の補正には、多重比較法が使用できます。関数 multcompare は、グループの平均 (処理効果) を多重対比較します。オプションとして、テューキーの HSD 法の基準 (既定のオプション)、ボンフェローニの方法、シェッフェの方法、フィッシャーの最小有意差 (LSD) 法、および t 検定に対するダンとシダックのアプローチがあります。この関数は、制御グループとの多重比較を実行するダネットの検定もサポートします。

グループの平均の多重比較を実行するには、構造体 stats を multcompare の入力引数として指定します。stats は、次の関数のいずれかから取得できます。

• anova1 — 1 因子 ANOVA

• anova2 — 2 因子 ANOVA

• anovan — 多因子 ANOVA

• aoctool — 対話型 ANCOVA

• kruskalwallis — 1 因子レイアウトについてのノンパラメトリック手法

• friedman — 2 因子レイアウトについてのノンパラメトリック手法

反復測定の多重比較法のオプションについては、multcompare (RepeatedMeasuresModel) を参照してください。

1 因子 ANOVA による多重比較

標本データを読み込みます。

load carsmall

MPG は各自動車のガロンあたりの走行マイル数、Cylinders は各自動車の気筒の数 (4、6 または 8) を表します。

気筒数が異なる自動車ではガロンあたりの走行マイル数 (mpg) の平均が異なるかどうかを検定します。また、多重比較検定に必要な統計量も計算します。

[p,~,stats] = anova1(MPG,Cylinders,"off");
p

p = 4.4902e-24

p 値は約 0 という小さい値なので、気筒数が異なる自動車ではガロンあたりの走行マイル数の平均が有意に異なることが強く示されます。

ボンフェローニの方法を使用して多重比較検定を実行し、どの気筒数で自動車の性能が異なるかを判別します。

[results,means,~,gnames] = multcompare(stats,"CriticalValueType","bonferroni");

図の青いバーは、4 気筒の自動車のグループを表しています。赤いバーは、他のグループを表しています。自動車の平均 mpg についてどの赤い比較区間も重なっていないので、気筒数が 4、6 または 8 の車では平均 mpg が有意に異なることがわかります。

多重比較の結果と該当するグループ名を table で表示します。

tbl = array2table([results,means],"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value","Mean","Standard Error"]);
tbl.("Group A")=gnames(tbl.("Group A"));
tbl.("Group B")=gnames(tbl.("Group B"))

tbl=3×8 table
    Group A    Group B    Lower Limit     A-B      Upper Limit     P-value       Mean     Standard Error
    _______    _______    ___________    ______    ___________    __________    ______    ______________

     {'4'}      {'6'}       4.8605       7.9418      11.023       3.3159e-08     29.53       0.63634    
     {'4'}      {'8'}       12.613       15.234      17.855       2.7661e-24    21.588        1.0913    
     {'6'}      {'8'}        3.894       7.2919       10.69        3.172e-06    14.296       0.86596    

results 行列の初めの 2 列には、どのグループを比較したかが示されています。たとえば、1 行目では 4 気筒の自動車と 6 気筒の自動車を比較しています。4 列目には、比較したグループにおける平均 mpg の差が示されています。3 列目と 5 列目には、グループ平均の差に関する 95% の信頼区間の下限と上限が示されています。最後の列には、検定の p 値が示されています。すべての "p" 値がほぼゼロなので、すべてのグループの平均 mpg がすべてのグループで異なっていることがわかります。

行列 means の 1 列目には、自動車の各グループについて平均 mpg の推定値が格納されます。2 列目には、推定値の標準誤差が格納されます。

3 因子 ANOVA の多重比較

標本データを読み込みます。

y = [52.7 57.5 45.9 44.5 53.0 57.0 45.9 44.0]';
g1 = [1 2 1 2 1 2 1 2];
g2 = ["hi" "hi" "lo" "lo" "hi" "hi" "lo" "lo"];
g3 = ["may" "may" "may" "may" "june" "june" "june" "june"];

y は応答ベクトル、g1、g2 および g3 はグループ化変数 (因子) です。各因子には 2 つの水準があり、y のすべての観測値は因子の水準の組み合わせによって識別されます。たとえば、観測値 y(1) は、因子 g1 の水準 1、因子 g2 の水準 hi および因子 g3 の水準 may に関連付けられています。同様に、観測値 y(6) は、因子 g1 の水準 2、因子 g2 の水準 hi および因子 g3 の水準 june に関連付けられています。

すべての因子水準について応答が同じであるか検定します。また、多重比較検定に必要な統計量も計算します。

[~,~,stats] = anovan(y,{g1 g2 g3},"Model","interaction", ...
    "Varnames",["g1","g2","g3"]);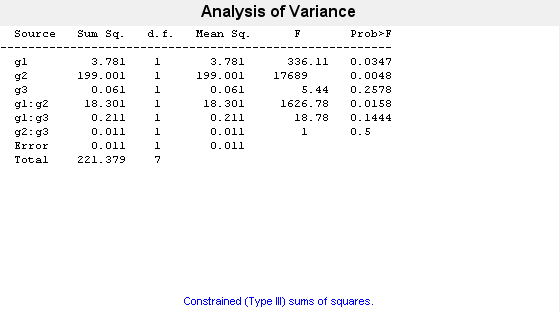

0.2578 という "p" 値は、因子 g3 の水準 may および june について平均応答が有意には異なっていないことを示しています。0.0347 という p 値は、因子 g1 の水準 1 および 2 について平均応答が有意に異なっていることを示しています。同様に、0.0048 という "p" 値は、因子 g2 の水準 hi および lo について平均応答が有意に異なっていることを示しています。

多重比較検定を実行し、因子 g1 および g2 についてどのグループが有意に異なるかを調べます。

[results,~,~,gnames] = multcompare(stats,"Dimension",[1 2]);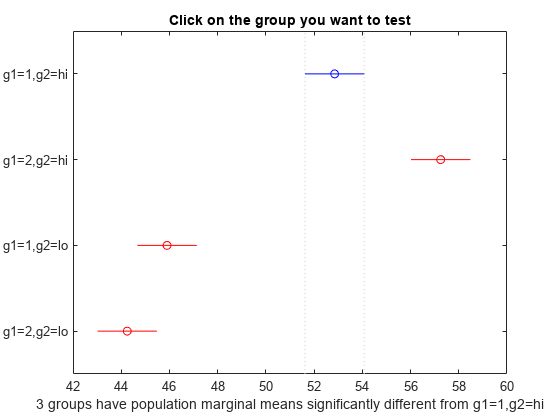

対応するグループの比較区間をクリックすると、他のグループについて検定を行うことができます。クリックしたバーは青になります。有意に異なるグループのバーは、赤になります。有意には異ならないグループのバーは、灰色になります。たとえば、g1 の水準 1 と g2 の水準 lo の組み合わせの比較区間をクリックすると、g1 の水準 2 と g2 の水準 lo の組み合わせの比較区間は重なるので灰色になります。逆に、他の比較区間は赤になり、有意に異なることを示します。

多重比較の結果と該当するグループ名を table で表示します。

tbl = array2table(results,"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"]);
tbl.("Group A")=gnames(tbl.("Group A"));
tbl.("Group B")=gnames(tbl.("Group B"))

tbl=6×6 table
       Group A           Group B        Lower Limit     A-B     Upper Limit     P-value 
    ______________    ______________    ___________    _____    ___________    _________

    {'g1=1,g2=hi'}    {'g1=2,g2=hi'}      -6.8604       -4.4      -1.9396       0.027249
    {'g1=1,g2=hi'}    {'g1=1,g2=lo'}       4.4896       6.95       9.4104       0.016983
    {'g1=1,g2=hi'}    {'g1=2,g2=lo'}       6.1396        8.6        11.06       0.013586
    {'g1=2,g2=hi'}    {'g1=1,g2=lo'}       8.8896      11.35        13.81       0.010114
    {'g1=2,g2=hi'}    {'g1=2,g2=lo'}        10.54         13        15.46      0.0087375
    {'g1=1,g2=lo'}    {'g1=2,g2=lo'}      -0.8104       1.65       4.1104        0.07375

関数 multcompare は、2 つのグループ化変数 g1 および g2 についてグループ (水準) の組み合わせを比較します。たとえば、この行列の 1 行目は、g1 の水準 1 と g2 の水準 hi の組み合わせが g1 の水準 2 と g2 の水準 hi の組み合わせと同じ平均応答値になっていることを示しています。この検定に対応する "p" 値は 0.0272 なので、平均応答が有意に異なっていることがわかります。この結果は、図からもわかります。青いバーは、g1 の水準 1 と g2 の水準 hi の組み合わせについて平均応答の比較区間を示しています。赤いバーは、他のグループの組み合わせについて平均応答の比較区間を示しています。どの赤いバーも青いバーと重なっていないので、g1 の水準 1 と g2 の水準 hi の組み合わせの平均応答が他のグループの組み合わせの平均応答と有意に異なっていることがわかります。

多重比較法

名前と値の引数 CriticalValueType を次の表のいずれかの値に設定して、多重比較法を指定します。

値	説明
"lsd"	フィッシャーの最小有意差法
"dunnett"	ダネットの検定
"tukey-kramer" または "hsd" (既定の設定)	テューキーの HSD 法
"dunn-sidak"	ダンとシダックのアプローチ
"bonferroni"	ボンフェローニの方法
"scheffe"	シェッフェの方法

この表は、棄却限界値の種類を保守度が低いものから順に並べた一覧です。検定ごとに多重比較の問題の防止レベルが異なります。

• "lsd" では保護は提供されません。

• "dunnett" では、制御グループとの比較について保護が提供されます。

• "tukey-kramer"、"dunn-sidak"、および "bonferroni" では、一対比較について保護が提供されます。

• "scheffe" では、一対比較と推定値のすべての線形結合の比較について保護が提供されます。

関数 multcompare は、名前と値の引数 CriticalValueType で指定された棄却限界値の種類に応じて異なるセットの帰無仮説 (H₀) と対立仮説 (H₁) を調べます。

• ダネットの検定 (CriticalValueType が "dunnett") では、制御グループとの多重比較を実行します。そのため、制御グループとの比較に関する帰無仮説と対立仮説は次のようになります。

  $$\begin{array}{l}{H}_0:\text{}{m}_i=m_0,\\ H_1:\text{}{m}_i\ne m_0,\end{array}$$

  ここで、m_i と m₀ はそれぞれグループ i と制御グループの推定値です。この関数は、制御グループ以外のすべてのグループについて H₀ と H₁ を複数回調べます。

• その他の検定では、multcompare はグループのすべての異なるペアについて多重対比較を実行します。グループ i とグループ j の一対比較の帰無仮説と対立仮説は次のようになります。

  $$\begin{array}{c}{H}_0:\text{}{m}_i=m_j,\\ H_1:\text{}{m}_i\ne m_j.\end{array}$$

フィッシャーの最小有意差法

最小有意差法を使用するには、CriticalValueType を "lsd" と指定します。この検定では次の検定統計量を使用します。

$$t=\frac{{\overline{y}}_i-{\overline{y}}_j}{\sqrt{MSE\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}}.$$

H₀:m_i = m_j は次の場合に棄却されます。

$$\left|{\overline{y}}_i-{\overline{y}}_j\right|>\underset{LSD}{\underbrace{t_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.,N-k}\sqrt{MSE\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}}}.$$

フィッシャーは、帰無仮説 H₀:m₁ = m₂ = ... = m_k が ANOVA の F 検定によって棄却された場合のみ LSD を実行し、多重比較を防ぐことを提案しています。この場合でも、LSD ではどの仮説も棄却されない可能性があります。また、一部のグループの平均に差がある場合でも、ANOVA では H₀ が棄却されない可能性がありますこのような状況になるのは、残りのグループ平均が等しいため F 検定統計量が有意でなくなる可能性があるからです。他の条件がないと、LSD では多重比較の問題を防止できません。

ダネットの検定

ダネットの検定を使用するには、CriticalValueType を "dunnett" と指定します。この検定は、制御グループとの多重比較を行うためのものです。名前と値の引数 ControlGroup を使用して、制御グループを指定できます。ダネットの検定の検定統計量は、グループ平均のソースによって異なります。1 因子 ANOVA から得たグループ平均を調べる場合、検定統計量は次のようになります。

$$t_i=\frac{{\overline{y}}_i-{\overline{y}}_0}{\sqrt{MSE\left(\frac{1}{n_i}+\frac{1}{n_0}\right)}}.$$

H₀ : m_i = m₀ は |t_i| < d の場合に棄却されます。関数 multcompare は、次の方程式を解くことで d を求めます。

$$F(d,\dots ,d|C,\nu )=P\left(\left|t_1\right|<d,\dots ,\left|t_p\right|<d\right)=1-\alpha ,$$

ここで、p は制御グループ以外のグループの数、F(⋯|C,ν) は相関行列 C と自由度 ν をもつ多変量 t 分布の累積分布関数 (cdf) です。

多因子 (n 因子) ANOVA では、n が大きい場合は d の計算速度が低下する可能性があります。計算を高速化するには、名前と値の引数 Approximate を true (多因子 ANOVA の既定値) に指定して近似法 ([5]) を使用します。近似法にはランダム性があります。結果を再現する場合は、multcompare を呼び出す前に関数 rng を使用して乱数シードを設定します。

テューキーの HSD 法

テューキーの HSD 法を使用するには、CriticalValueType を "Tukey-Kramer" または "hsd" と指定します。検定は、スチューデント化された範囲分布に基づいて行われます。H₀:m_i = m_j は次の場合に棄却されます。

$$\left|t\right|=\frac{\left|{\overline{y}}_i-{\overline{y}}_j\right|}{\sqrt{MSE\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}}>\frac{1}{\sqrt{2}}{q}_{\alpha ,k,N-k,}$$

ここで、$$q_{\alpha ,k,N-k}$$ は、パラメーター k および自由度 N - k でスチューデント化された範囲分布の上位 100*(1 - α) 番目の百分位数です。k はグループ数 (処理数または周辺平均)、N は観測値の総数です。

テューキーの HSD 法は、平衡型の 1 因子 ANOVA および標本サイズが等しい同様の手順に最適です。サイズの異なる標本による 1 因子 ANOVA の場合も、標準的であることが実証されています。まだ証明されていないテューキー クレーマーの推測によると、不平衡共変量値をもつ共分散の分析に見られるように、比較対象の数量が相関をもつ問題に対しても正確です。

ダンとシダックのアプローチ

ダンとシダックのアプローチを使用するには、CriticalValueType を "dunn-sidak" と指定します。このアプローチでは、ダンにより提唱されシダックにより証明された調整を多重比較に対して行った後で t 分布の棄却限界値を使用します。H₀:m_i = m_j は次の場合に棄却されます。

$$\left|t\right|=\frac{\left|{\overline{y}}_i-{\overline{y}}_j\right|}{\sqrt{MSE\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}}>t_{1-\eta /2,v,}$$

ここで

$$\eta =1-{\left(1-\alpha \right)}^{{}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\left(\begin{array}{l}k\\ 2\end{array}\right)$}\right.}}$$

k はグループ数です。この過程は、ボンフェローニのアルゴリズムに似ていますが、それほど保守的ではありません。

ボンフェローニの方法

ボンフェローニの方法を使用するには、CriticalValueType を "bonferroni" と指定します。この方法では、多重比較を補正するように調整した後でスチューデント t 分布の棄却限界値を使用します。H₀:m_i = m_j は $$\alpha /2\left(\begin{array}{l}k\\ 2\end{array}\right)$$ という有意水準で棄却されます。k は次の場合のグループ数です。

$$\left|t\right|=\frac{\left|{\overline{y}}_i-{\overline{y}}_j\right|}{\sqrt{MSE\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}}>t_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2\left(\begin{array}{c}k\\ 2\end{array}\right)$}\right.,N-k,}$$

ここで、N は観測値の総数、k はグループ数 (周辺平均) です。このアルゴリズムは保守的ですが、通常、Scheffé アルゴリズムほど保守的ではありません。

シェッフェの方法

シェッフェの方法を使用するには、CriticalValueType を "scheffe" と指定します。棄却限界値は F 分布から導き出されます。H₀:m_i = m_j は次の場合に棄却されます。

$$\frac{\left|{\overline{y}}_i-{\overline{y}}_j\right|}{\sqrt{MSE\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}}>\sqrt{\left(k-1\right)F_{k-1,N-k,\alpha }}$$

この方法では、平均のすべての線形結合の比較について同時信頼水準が与えられます。ペアの間の単純な差を比較するための、保守的なアルゴリズムです。

参照

[1] Milliken G. A. and D. E. Johnson. Analysis of Messy Data. Volume I: Designed Experiments. Boca Raton, FL: Chapman & Hall/CRC Press, 1992.

[2] Neter J., M. H. Kutner, C. J. Nachtsheim, W. Wasserman. 4th ed. Applied Linear Statistical Models.Irwin Press, 1996.

[3] Hochberg, Y., and A. C. Tamhane. Multiple Comparison Procedures. Hoboken, NJ: John Wiley & Sons, 1987.

[4] Dunnett, Charles W. “A Multiple Comparison Procedure for Comparing Several Treatments with a Control.” Journal of the American Statistical Association, vol. 50, no. 272, Dec. 1955, pp. 1096–121.

[5] Krishnaiah, Paruchuri R., and J. V. Armitage. "Tables for multivariate t distribution." Sankhyā: The Indian Journal of Statistics, Series B (1966): 31-56.

参考

multcompare | anova1 | anova2 | anovan | aoctool | kruskalwallis | friedman

関連するトピック

• 1 因子 ANOVA の実行
• 2 因子 ANOVA の実行