多因子 ANOVA

多因子 ANOVA の紹介

関数 anovan を使用すると、多因子 ANOVA を実行できます。一連のデータの平均が複数因子のグループ (レベル) に関して異なるかどうかを判別するには、多因子 ANOVA を使用します。既定の設定では、anovan はすべてのグループ化変数を固定効果として扱います。変量効果がある ANOVA の例については、変量効果のある分散分析 (ANOVA)を参照してください。反復測定については、fitrm と ranova を参照してください。

多因子 ANOVA は 2 因子 ANOVA の汎化です。たとえば、因子が 3 つあるモデルは次のように記述できます。

$$y_{ijkr}=\mu +{\alpha }_i+{\beta }_j+{\gamma }_k+{(\alpha \beta )}_{ij}+{(\alpha \gamma )}_{ik}+{(\beta \gamma )}_{jk}+{(\alpha \beta \gamma )}_{ijk}+{\epsilon }_{ijkr,}$$

ここで

• y_ijkr は応答変数の観測値です。i は因子 A のグループ i を表します (i = 1, 2, ..., I)。j は因子 B のグループ j を表します (j = 1, 2, ..., J)。k は因子 C のグループ k を表します。r は複製数を表します (r = 1, 2, ..., R)。定数 R について観測値の総数は N = I*J*K*R ですが、観測値の数は因子のグループの各組み合わせについて同じである必要はありません。

• μ は全体の平均です。

• α_i は、因子 A に起因する、全体の平均 μ に対する因子 A のグループの偏差です。α_i の合計は 0 になります。

  $${\displaystyle {\sum }_{i=1}^I{\alpha }_i}=0.$$

• β_j は、因子 B に起因する、全体の平均 μ に対する因子 B のグループの偏差です。β_j の合計は 0 になります。

  $${\displaystyle {\sum }_{j=1}^J{\beta }_j}=0.$$

• γ_k は、因子 C に起因する、全体の平均 μ に対する因子 C のグループの偏差です。γ_k の合計は 0 になります。

  $${\displaystyle {\sum }_{k=1}^K{\gamma }_k}=0.$$

• (αβ)_ij は、因子 A および B の間の交互作用項です。(αβ)_ij をいずれかのインデックスについて合計すると 0 になります。

  $${\displaystyle {\sum }_{i=1}^I{\left(\alpha \beta \right)}_{ij}}={\displaystyle {\sum }_{j=1}^J{\left(\alpha \beta \right)}_{ij}}=0.$$

• (αγ)_ik は、因子 A および C の間の交互作用項です。(αγ)_ik をいずれかのインデックスについて合計すると 0 になります。

  $${\displaystyle {\sum }_{i=1}^I{\left(\alpha \gamma \right)}_{ik}}={\displaystyle {\sum }_{k=1}^K{\left(\alpha \gamma \right)}_{ik}}=0.$$

• (βγ)_jk は、因子 B および C の間の交互作用項です。(βγ)_jk をいずれかのインデックスについて合計すると 0 になります。

  $${\displaystyle {\sum }_{j=1}^J{\left(\beta \gamma \right)}_{jk}}={\displaystyle {\sum }_{k=1}^K{\left(\beta \gamma \right)}_{jk}}=0.$$

• (αβγ)_ijk は、因子 A、B および C の間の 3 次交互作用項です。αβγ(_ijk) をいずれかのインデックスについて合計すると 0 になります。

  $${\displaystyle {\sum }_{i=1}^I{\left(\alpha \beta \gamma \right)}_{ijk}}={\displaystyle {\sum }_{j=1}^J{\left(\alpha \beta \gamma \right)}_{ijk}}={\displaystyle {\sum }_{k=1}^K{\left(\alpha \beta \gamma \right)}_{ijk}}=0.$$

• ε_ijkr はランダム外乱です。これらは、独立、正規分布、および一定の分散になっていると仮定されます。

3 因子 ANOVA では、因子 A、B、C の効果と応答変数 y に対する交互作用に関する仮説を検定します。因子 A の各グループにおける平均応答の等価性について、仮説は次のようになります。

$$\begin{array}{l}{H}_0:{\alpha }_1={\alpha }_2\cdots ={\alpha }_I\\ H_1:\text{ at least one }{\alpha }_i\text{ is different},i=1,2,\mathrm{...},I.\end{array}$$

因子 B の各グループにおける平均応答の等価性について、仮説は次のようになります。

$$\begin{array}{l}{H}_0:{\beta }_1={\beta }_2=\cdots ={\beta }_J\\ H_1:\text{ at least one }{\beta }_j\text{ is different, }j=1,2,\mathrm{...},J.\end{array}$$

因子 C の各グループにおける平均応答の等価性について、仮説は次のようになります。

$$\begin{array}{l}{H}_0:{\gamma }_1={\gamma }_2=\cdots ={\gamma }_K\\ H_1:\text{ at least one }{\gamma }_k\text{ is different},k=1,2,\mathrm{...},K.\end{array}$$

因子の交互作用について、仮説は次のようになります。

$$\begin{array}{l}{H}_0:{\left(\alpha \beta \right)}_{ij}=0\\ H_1:\text{at least one }{\left(\alpha \beta \right)}_{ij}\ne 0\end{array}$$

$$\begin{array}{l}{H}_0:{\left(\alpha \gamma \right)}_{ik}=0\\ H_1:\text{at least one }{\left(\alpha \gamma \right)}_{ik}\ne 0\\ \\ H_0:{\left(\beta \gamma \right)}_{jk}=0\\ H_1:\text{at least one }{\left(\beta \gamma \right)}_{jk}\ne 0\\ \\ H_0:{\left(\alpha \beta \gamma \right)}_{ijk}=0\\ H_1:\text{at least one }{\left(\alpha \beta \gamma \right)}_{ijk}\ne 0\end{array}$$

この表記法では、(αβ)_ij のように 2 つの添字があるパラメーターは 2 つの因子の交互作用効果を表します。パラメーター (αβγ)_ijk は、3 次交互作用を表します。ANOVA モデルは、パラメーターの完全なセットまたは任意のサブセットをもつことができますが、それらの因子にのより単純な項を含まない限り、複雑な交互作用項を一般には含みません。たとえば、通常はすべての 2 次相互項を含まないときは 3 次相互項は含みません。

多因子 ANOVA 用データの準備

anova1 および anova2 と異なり、anovan ではデータが表形式になっている必要はありません。代わりに、応答観測値のベクトルと各因子に対応する値を含む別々のベクトル (あるいはテキスト配列) を要求します。この入力データ形式は、2 因子より多いとき、あるいは因子の組み合せあたりの観測値が一定でないときには、行列よりも便利です。

$$\begin{array}{ccccccccccc}y& =& [& y_1,& y_2,& y_3,& y_4,& y_5,& \cdots ,& y_N& {]}^{\prime }\\ & & & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow & & \uparrow & \\ g1& =& \{& \text{'}A\text{'},& \text{'}A\text{'},& \text{'}C\text{'},& \text{'}B\text{'},& \text{'}B\text{'},& \cdots ,& \text{'}D\text{'}& \}\\ g2& =& [& 1& 2& 1& 3& 1& \cdots ,& 2& ]\\ g3& =& \{& \text{'}\text{hi}\text{'},& \text{'}\text{mid}\text{'},& \text{'}\text{low}\text{'},& \text{'}\text{mid}\text{'},& \text{'}\text{hi}\text{'},& \cdots ,& \text{'}\text{low}\text{'}& \}\end{array}$$

多因子 ANOVA の実行

この例では、自動車データに対して多因子 ANOVA を実行する方法を示します。データには、1970 ～ 1982 年に製造された 406 台の自動車に関する燃費などの情報が含まれています。

標本データを読み込みます。

load carbig

この例の 4 つの変数に注目します。MPG は、406 種類の自動車の 1 ガロンあたりのマイル数です (NaN と記述されている欠損値を含むものもあります)。その他の 3 つの変数は、cyl4 (4 気筒が搭載された車かどうか)、org (ヨーロッパ、日本、米国製)、when (期間の前期、中期、後期に製造) の 3 つの因子です。

3 次交互作用と Type 3 の二乗和を要求して、完全なモデルを当てはめます。

varnames = {'Origin';'4Cyl';'MfgDate'};
anovan(MPG,{org cyl4 when},3,3,varnames);

多くの項に、フル ランクでないことを示す # という記号が付けられ、それらのうち 1 つは自由度がゼロで、p 値が欠落しています。これは、因子の組み合せが失われていたり、モデルが高次項をもつときに発生することがあります。この場合、下記のクロス集計により、期間の初期にヨーロッパで製造された 4 気筒以外の自動車は存在しないことが tbl(2,1,1) の 0 からわかります。

[tbl,chi2,p,factorvals] = crosstab(org,when,cyl4)

tbl = 
tbl(:,:,1) =

    82    75    25
     0     4     3
     3     3     4


tbl(:,:,2) =

    12    22    38
    23    26    17
    12    25    32

chi2 = 207.7689

p = 8.0973e-38

factorvals=3×3 cell array
    {'USA'   }    {'Early'}    {'Other'   }
    {'Europe'}    {'Mid'  }    {'Four'    }
    {'Japan' }    {'Late' }    {0x0 double}

その結果、3 次交互作用の影響を推定することは不可能で、3 次交互作用項をモデルに含めると、近似が特異になります。

ANOVA 表から得られる限られた情報でも、3 次交互作用が p 値 0.699 をもち、有意でないことがわかります。

2 次交互作用のみを調べます。

[p,tbl2,stats,terms] = anovan(MPG,{org cyl4 when},2,3,varnames);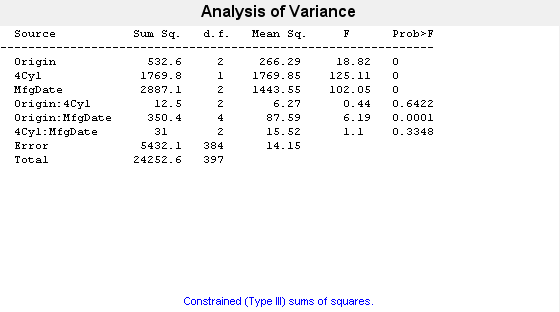

terms

terms = 6×3

     1     0     0
     0     1     0
     0     0     1
     1     1     0
     1     0     1
     0     1     1

これですべての項を見積もることができます。交互作用項 4 (Origin*4Cyl) と交互作用項 6 (4Cyl*MfgDate) に対する p 値は、典型的なカットオフ値 0.05 よりもかなり大きく、これらの項が有意でないことを示しています。これらの項を省略し、影響を誤差の項に集めることができます。出力変数 terms は、それぞれが項を表すビット パターンであるコードの行列を出力します。

terms から項の入力を削除して、モデルから項を省略します。

terms([4 6],:) = []

terms = 4×3

     1     0     0
     0     1     0
     0     0     1
     1     0     1

anovan を再度実行します。このときは結果のベクトルをモデル引数として指定します。因子の多重比較に必要な統計量も返されます。

[~,~,stats] = anovan(MPG,{org cyl4 when},terms,3,varnames)

stats = struct with fields:
         source: 'anovan'
          resid: [3.1235 0.1235 3.1235 1.1235 2.1235 0.1235 -0.8765 -0.8765 -0.8765 0.1235 NaN NaN NaN NaN NaN 0.1235 -0.8765 NaN 0.1235 -0.8765 -2.3832 7.1235 3.1235 6.1235 0.6168 1.2857 0.2857 -0.7143 0.2857 1.2857 6.1235 -4.8765 ... ] (1x406 double)
         coeffs: [18x1 double]
            Rtr: [10x10 double]
       rowbasis: [10x18 double]
            dfe: 388
            mse: 14.1056
    nullproject: [18x10 double]
          terms: [4x3 double]
        nlevels: [3x1 double]
     continuous: [0 0 0]
         vmeans: [3x1 double]
       termcols: [5x1 double]
     coeffnames: {18x1 cell}
           vars: [18x3 double]
       varnames: {3x1 cell}
       grpnames: {3x1 cell}
        vnested: []
            ems: [5x5 double]
          denom: []
        dfdenom: []
        msdenom: []
         varest: []
          varci: []
       txtdenom: []
         txtems: []
        rtnames: []

ここでは、これらの車の燃費が 3 つすべての因子に関連し、製造日の影響が車の製造場所に依存することを示すより単純なモデルを得ることができました。

生産国と気筒について多重比較を実行します。

[results,~,~,gnames] = multcompare(stats,'Dimension',[1,2]);

多重比較の結果と該当するグループ名を table で表示します。

tbl = array2table(results,"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"]);
tbl.("Group A") = gnames(tbl.("Group A"));
tbl.("Group B") = gnames(tbl.("Group B"))

tbl=15×6 table
              Group A                         Group B               Lower Limit      A-B      Upper Limit     P-value  
    ____________________________    ____________________________    ___________    _______    ___________    __________

    {'Origin=USA,4Cyl=Other'   }    {'Origin=Japan,4Cyl=Other' }      -5.4891      -3.8412      -2.1932      4.2334e-10
    {'Origin=USA,4Cyl=Other'   }    {'Origin=Europe,4Cyl=Other'}      -4.4146      -2.7251      -1.0356      6.2974e-05
    {'Origin=USA,4Cyl=Other'   }    {'Origin=USA,4Cyl=Four'    }      -9.9992      -8.5828      -7.1664               0
    {'Origin=USA,4Cyl=Other'   }    {'Origin=Japan,4Cyl=Four'  }      -14.024      -12.424      -10.824               0
    {'Origin=USA,4Cyl=Other'   }    {'Origin=Europe,4Cyl=Four' }      -12.898      -11.308       -9.718               0
    {'Origin=Japan,4Cyl=Other' }    {'Origin=Europe,4Cyl=Other'}     -0.71714        1.116       2.9492          0.5085
    {'Origin=Japan,4Cyl=Other' }    {'Origin=USA,4Cyl=Four'    }      -7.3655      -4.7417      -2.1179      3.8678e-06
    {'Origin=Japan,4Cyl=Other' }    {'Origin=Japan,4Cyl=Four'  }      -9.9992      -8.5828      -7.1664               0
    {'Origin=Japan,4Cyl=Other' }    {'Origin=Europe,4Cyl=Four' }      -9.7464      -7.4668      -5.1872      1.4557e-20
    {'Origin=Europe,4Cyl=Other'}    {'Origin=USA,4Cyl=Four'    }      -8.5396      -5.8577      -3.1757      6.9888e-09
    {'Origin=Europe,4Cyl=Other'}    {'Origin=Japan,4Cyl=Four'  }      -12.052      -9.6988      -7.3459               0
    {'Origin=Europe,4Cyl=Other'}    {'Origin=Europe,4Cyl=Four' }      -9.9992      -8.5828      -7.1664               0
    {'Origin=USA,4Cyl=Four'    }    {'Origin=Japan,4Cyl=Four'  }      -5.4891      -3.8412      -2.1932      4.2334e-10
    {'Origin=USA,4Cyl=Four'    }    {'Origin=Europe,4Cyl=Four' }      -4.4146      -2.7251      -1.0356      6.2974e-05
    {'Origin=Japan,4Cyl=Four'  }    {'Origin=Europe,4Cyl=Four' }     -0.71714        1.116       2.9492          0.5085

参考

anova | anova1 | anovan | multcompare | kruskalwallis

関連する例

• 変量効果のある分散分析 (ANOVA)

詳細

• 1 因子 ANOVA
• 2 因子 ANOVA
• 多重比較
• ノンパラメトリック手法