共分散分析

共分散分析の紹介

共分散分析は、応答 (y、予測される変数) と予測子 (x、予測に使われる変数) をもつグループ化されたデータを分析するための手法です。共分散分析を使用して、グループ間で変化する可能性のある直線の係数により、x の線形関数として y をモデル化することができます。

共分散分析ツール

関数 aoctool は、共分散分析 (ANOCOVA) モデルを使った近似と予測のための対話形式のグラフィカルな環境を開きます。これは、i 番目のグループについて次のモデルで近似します。

同じ平均	y = α + ε
異なる平均	y = (α + αi) + ε
同じライン	y = α + βx + ε
平行ライン	y = (α + αi) + βx + ε
異なるライン	y = (α + αi) + (β + βi)x + ε

たとえば、平行ラインのモデルにおいて、切片はグループごとに異なりますが、傾きはグループごとに同一です。同じ平均のモデルでは、共通の切片がありますが傾きはありません。グループ係数を決定するには、次の制約を設定します。

$${\displaystyle \sum {\alpha }_j={\displaystyle \sum {\beta }_j=0}}$$

次の節では、aoctool の使用について調べます。

1. データを読み込みます。Statistics and Machine Learning Toolbox™ の carsmall.mat というデータ セットには、1970 年、1976 年および 1982 年の自動車に関する情報が含まれています。この例では、自動車の重さと燃費の関係、およびこの関係が年によって変化したかどうかを調べます。デモを開始するには、データ セットを読み込みます。

   load carsmall

   ワークスペース ブラウザーは、データ セットの変数を表示します。

   

   ユーザーのデータについて aoctool を使用することもできます。

2. ツールを起動します。次のコマンドは、aoctool を呼び出し、Model_Year に定義された 3 つのモデル グループのそれぞれに対して、Weight と MPG の列ベクトルに別々のラインを近似させます。初期の当てはめでは、変数 y (MPG) を変数 x (Weight) の線形関数としてモデル化します。

   [h,atab,ctab,stats] = aoctool(Weight,MPG,Model_Year);
   

   aoctool の呼び出しに関する詳細は、関数 aoctool のリファレンス ページを参照してください。

3. 出力を調べます。グラフィカルな出力は、次のプロットを表示するメイン ウィンドウと、係数推定表と分散分析表で構成されます。プロットにおいて、各 Model_Year のグループは別のラインをもちます。各グループのデータ点は、同じ色と記号によりエンコードされ、各グループに対する近似は、データ点と同じ色になります。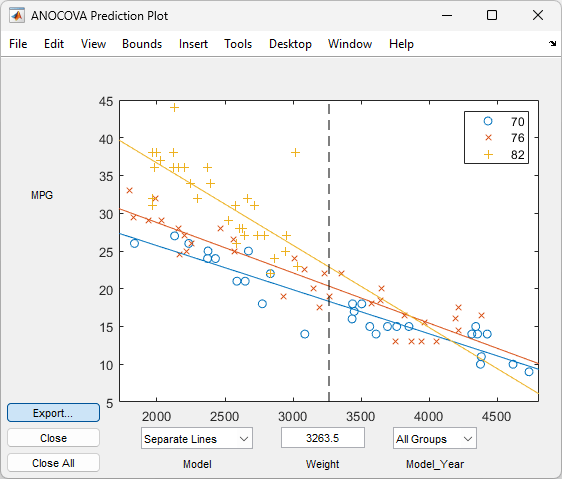

   

   3 本の線の係数は、ANOCOVA Coefficients と示されます。各グループの傾きが約 -0.0078 で、偏差が小さいことがわかります。

   • モデル年 1970: y = (45.9798 – 8.5805) + (–0.0078 + 0.002)x + ε

   • モデル年 1976: y = (45.9798 – 3.8902) + (–0.0078 + 0.0011)x + ε

   • モデル年 1982: y = (45.9798 + 12.4707) + (–0.0078 – 0.0031)x + ε

   

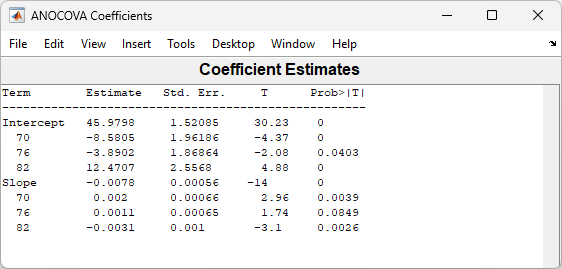
   3 つの近似線は、ほとんど同じ傾きをもつため、これらが本当に同じかどうか疑問に思うでしょう。Model_Year*Weight の交互作用は、傾きの差を表し、ANOVA の表はこの項の有意差の検定を表示します。F 統計量が 5.23 で p 値が 0.0072 であるので、傾きには有意差があります。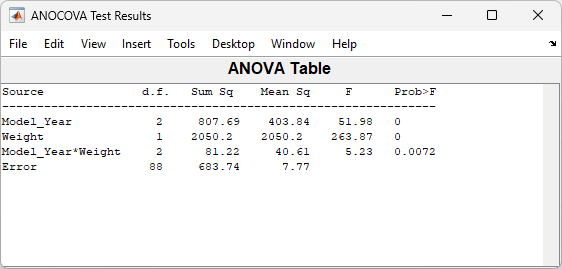

   

4. 傾きが同じになるよう、制限をかけます。傾きが同一に制限されているときの近似を調べるために、[ANOCOVA 予測プロット] ウィンドウに戻って、[モデル] ポップアップを使って [平行ライン] モデルを選択します。ウィンドウは、更新され次のグラフを表示します。

   

   この近似も妥当に見えますが、[異なるライン] モデルより明らかに悪いことがわかります。再度 [モデル] ポップアップ メニューを使って、オリジナルのモデルに戻ります。

信頼限界

共分散分析ツール の例は、各 Model_Year に対する MPG と Weight の関係を推定します。これらの推定はどれほど正確でしょうか。調べるために、一度に 1 つのグループを調べることにより、近似の上に信頼限界を重ね合わせることができます。

1. Figure の右下にある [Model_Year] メニューの設定を [すべてのグループ] から 82 に変更します。他のグループのデータと当てはめがグレー表示になり、信頼限界が 82 年の当てはめの周辺に表示されます。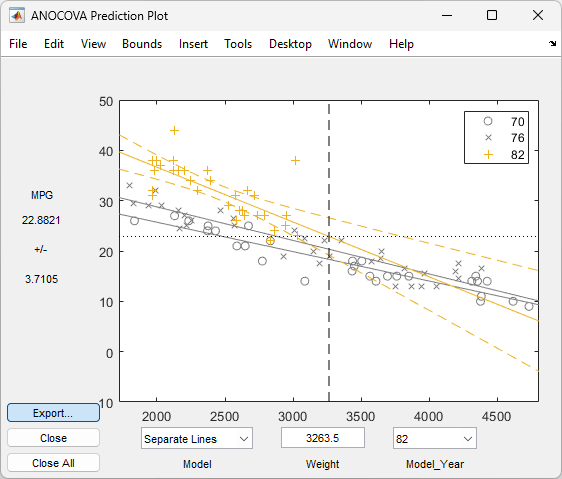

   

   破線は、モデル年 82 について当てはめた線の周辺で包絡線を形成します。正しい関係が線形であると仮定すると、これらの境界は正しい線について 95% の信頼領域を与えます。その他のモデル年に対する近似は、2000 と 3000 の間の Weight の値に対しては信頼限界の外にあることに注意してください。

2. 平均の応答値を推定するだけでなく、新規の観測値に対する応答値を予測できることに価値がある場合があります。関数 aoctool の [信頼限界] メニューを使用して、[ライン] から [観測値] への信頼限界の定義を変更します。結果となる広い間隔は、パラメーター推定の不確実性と新規の観測の無作為性を反映しています。

   

   関数 polytool のように、関数 aoctool には Weight を操作するために使用できる十字があり、y 軸の更新に従い、推定と信頼限界を見ることができます。これらの値は、[すべてのグループ] ではなく、1 つのグループが選択されたときにのみ表示されます。

多重比較

aoctool の stats 出力を関数 multcompare の入力として使うことによって、多重比較検定を行うことができます。関数 multcompare は、傾き、切片、母集団周辺平均 (各グループに対する平均の重みの予測された MPG ) を検定することができます。共分散分析ツール の例は、傾きは、3 つが同じではないことを示しますが、2 つは同じであり、他の 1 つのみが異なるのでしょうか。この仮説を検定できます。

multcompare(stats,0.05,"on","","s")

    1.0000    2.0000   -0.0012    0.0008    0.0029    0.6043
    1.0000    3.0000    0.0013    0.0051    0.0088    0.0049
    2.0000    3.0000    0.0005    0.0042    0.0079    0.0209

この行列は、グループ 1 と 2 (1970 と 1976) の切片の推定された差が 0.0008で、差に対する信頼区間が [-0.0012, 0.0029] であることを示します。これらの 2 つには有意差はありません。しかし、1982 の切片と残りの 2 つのそれぞれとの間には有意差があります。グラフは同じ情報を示します。

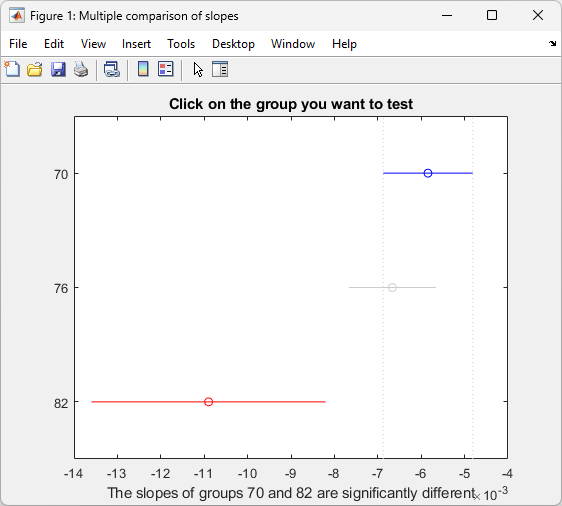
stats 構造体は、関数 aoctool の最初の呼び出しで作成されたため、(典型的に別々の直線のモデルの) 初期のモデルの当てはめに基づくことに注意してください。モデルを対話形式で変更し、新規モデルに基づいて多重比較したい場合は、aoctool を再度実行して、別の stats 構造体を取得し、新規モデルを初期モデルとして指定しなければなりません。

参考

aoctool | multcompare