replaceFilters

Replace existing filters with new filters in Filter Analyzer app

Since R2024a

Syntax

replaceFilters(fa,filt1,...,filtn)

replaceFilters(___,Name=Value)

Description

replaceFilters(fa,filt1,...,filtn) replaces all the filters in the Filter Analyzer app fa with new filters. The number of specified filters must be equal to the total number of filters currently in the app. If you want to replace only a subset of the filters, use the FilterNames argument to specify which ones.

example

replaceFilters(___,Name=Value) specifies options using name-value arguments in addition to the input arguments from the previous syntax.

example

Examples

collapse all

Replace Existing Filters

Open Live Script

Start the Filter Analyzer app with one lowpass filter.

d1 = designfilt("lowpassfir", ...
    PassbandFrequency=0.45,StopbandFrequency=0.55);
fa = filterAnalyzer(d1,FilterNames="LP");

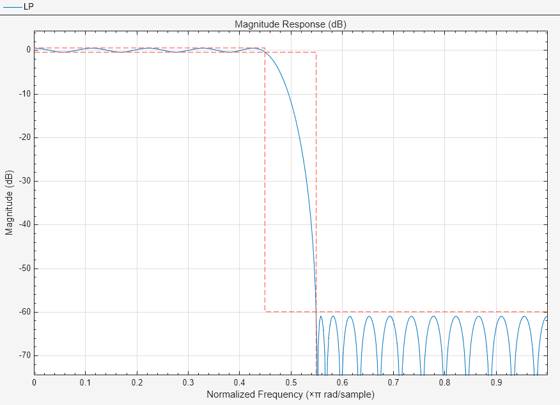
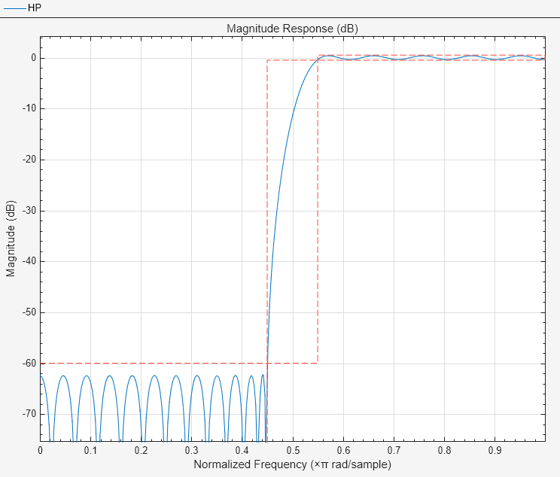
Replace the lowpass filter with a highpass filter.

d2 = designfilt("highpassfir", ...
    PassbandFrequency=0.55,StopbandFrequency=0.45);
replaceFilters(fa,d2,FilterNames="LP")
renameFilters(fa,"LP","HP")

Input Arguments

collapse all

`fa` — Filter Analyzer app handle
`filterAnalyzer` object

Filter Analyzer app handle, specified as a filterAnalyzer object.

`filt` — Input filters
coefficient matrices | cell array | `digitalFilter` object | filter System object™

Input filter, specified as coefficient matrices, a cell array, a digitalFilter object, or a filter System object.

For more information, see Import Filter on the Filter Analyzer page..

Example: b = [1 3 3 1]/6 and a = [3 0 1 0]/3 together specify a third-order lowpass Butterworth filter with a normalized 3-dB frequency of 0.5π rad/sample.

Example: sos2ctf([2 4 2 6 0 2; 3 3 0 6 0 0]) specifies a third-order lowpass Butterworth filter with a normalized 3-dB frequency of 0.5π rad/sample.

Example: d = designfilt("lowpassiir",FilterOrder=3,HalfPowerFrequency=0.5) specifies a third-order lowpass Butterworth filter with a normalized 3-dB frequency of 0.5π rad/sample.

Example: hd = design(fdesign.lowpass,"butter",SystemObject=true) specifies a lowpass Butterworth filter System object.

Filter Coefficients

You can use Filter Analyzer to analyze filters specified as numerator and denominator coefficients. If you specify the coefficients as the L-row matrices

$B = [\begin{matrix} b_{11} & b_{12} & \dots & b_{1, m + 1} \\ b_{21} & b_{22} & \dots & b_{2, m + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ b_{L 1} & b_{L 2} & \dots & b_{L, m + 1} \end{matrix}], A = [\begin{matrix} a_{11} & a_{12} & \dots & a_{1, n + 1} \\ a_{21} & a_{22} & \dots & a_{2, n + 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{L 1} & a_{L 2} & \dots & a_{L, n + 1} \end{matrix}],$

Filter Analyzer assumes you have specified the filter as a sequence of L cascaded transfer functions (CTF), such that the full transfer function of the filter is

$H (z) = \frac{b_{11} + b_{12} z^{- 1} + \dots + b_{1, m + 1} z^{- m}}{a_{11} + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times \frac{b_{21} + b_{22} z^{- 1} + \dots + b_{2, m + 1} z^{- m}}{a_{21} + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times \frac{b_{L 1} + b_{L 2} z^{- 1} + \dots + b_{L, m + 1} z^{- m}}{a_{L 1} + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}},$

where m ≥ 0 is the numerator order of the filter and n ≥ 0 is the denominator order.

If L = 1, then B and A are row vectors that specify the transfer function of an IIR filter.
If you specify both B and A as column vectors, Filter Analyzer assumes they represent the transfer function of an IIR filter.
If B is a scalar, Filter Analyzer assumes you specified the filter as a cascade of all-pole IIR filters with each section having a scaling gain equal to B.
If A is a scalar, Filter Analyzer assumes you specified the filter as a cascade of FIR filters with each section having a scaling gain equal to 1/A.

Note

To convert second-order section matrices to cascaded transfer functions, use the sos2ctf function.
To convert a zero-pole-gain filter representation to cascaded transfer functions, use the zp2ctf function.

Coefficients and Gain

If you have a scaling gain separate from the coefficient values, you can enter it in Filter Analyzer using the Import Filters dialog box. At the command line, you can specify the coefficients and gain as a cell array of the form {B,A,g}, where B and A are as defined in the Filter Coefficients section.

The gain can be a scalar overall gain or a vector of section gains.

If the gain is a scalar, Filter Analyzer applies the value uniformly to all the cascade filter sections.
If the gain is a vector, it must have one more element than the number of filter sections in the cascade. Filter Analyzer applies a scale value to each of the filter sections and applies the last value uniformly to all the filter sections.

If you specify the coefficient matrices and gain vector as

Filter Analyzer uses the transfer function

$H (z) = g_{S} (g_{1} \frac{b_{11} + b_{12} z^{- 1} + \dots + b_{1, m + 1} z^{- m}}{a_{11} + a_{12} z^{- 1} + \dots + a_{1, n + 1} z^{- n}} \times g_{2} \frac{b_{21} + b_{22} z^{- 1} + \dots + b_{2, m + 1} z^{- m}}{a_{21} + a_{22} z^{- 1} + \dots + a_{2, n + 1} z^{- n}} \times \dots \times g_{L} \frac{b_{L 1} + b_{L 2} z^{- 1} + \dots + b_{L, m + 1} z^{- m}}{a_{L 1} + a_{L 2} z^{- 1} + \dots + a_{L, n + 1} z^{- n}}) .$

`digitalFilter` Objects

You can use Filter Analyzer to analyze digitalFilter objects. Use designfilt to generate or edit digital filters based on frequency-response specifications.

Filter System Objects

If you have DSP System Toolbox™, you can use Filter Analyzer to analyze these filter System objects.

System object
`dsp.AllpassFilter`
`dsp.AllpoleFilter`
`dsp.CICCompensationDecimator`
`dsp.CICCompensationInterpolator`
`dsp.CICDecimator`
`dsp.CICInterpolator`
`dsp.ComplexBandpassDecimator` (since R2024b)
`dsp.CoupledAllpassFilter`
`dsp.DCBlocker` (since R2024b)
`dsp.Delay`
`dsp.Differentiator`
`dsp.DigitalDownConverter`
`dsp.DigitalUpConverter`
`dsp.FIRDecimator`
`dsp.FIRFilter`
`dsp.FIRHalfbandDecimator`
`dsp.FIRHalfbandInterpolator`
`dsp.FIRInterpolator`
`dsp.FIRRateConverter`
`dsp.FarrowRateConverter`
`dsp.FilterCascade`
`dsp.FourthOrderSectionFilter` — Filter Analyzer does not support fixed-point arithmetic for this object
`dsp.HighpassFilter`
`dsp.IIRFilter`
`dsp.IIRHalfbandDecimator`
`dsp.IIRHalfbandInterpolator`
`dsp.LowpassFilter`
`dsp.NotchPeakFilter` — Filter Analyzer does not support fixed-point arithmetic for this System object
`dsp.ParallelFilter`
`dsp.SOSFilter`
`dsp.VariableBandwidthFIRFilter`
`dsp.VariableBandwidthIIRFilter`

If you also have DSP HDL Toolbox™, you can use Filter Analyzer to analyze these filter System objects.

System object
`dsphdl.FIRFilter` (DSP HDL Toolbox) (since R2024b)
`dsphdl.BiquadFilter` (DSP HDL Toolbox) (since R2024b)

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: FilterNames=["LP" "HP"],SampleRates=[150 3e3]

`Arithmetic` — Arithmetic type of filter System objects
`"double"` (default) | `"single"` | `"fixed"`

Arithmetic type of filter System objects, specified as one of "double", "single", or "fixed". If you do not specify this argument, and the filter System objects are in an unlocked state, Filter Analyzer assumes the filters are double precision.

Data Types: char | string

`FilterNames` — Names of filters to replace
string vector

Names of filters to replace, specified as a string vector. Filter names are the names that identify the different filters in the app Filters table.

Example: ["LPbutter" "LPelliptic"]

Data Types: char | string

`SampleRates` — Filter sample rates
`1` (default) | scalar | vector

Filter sample rates, specified as a scalar or vector of values specified in Hz.

If SampleRates is a scalar, the specified value applies to all filters.
If SampleRates is a vector, it must have a number of elements equal to the number of filters.

This argument does not apply if one or more filters are objects with a sample rate.

Example: [150 3e3]

Version History

Introduced in R2024a

replaceFilters

Syntax

Description