このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

fitrkernel

ランダムな特徴量拡張を使用してガウス カーネル回帰モデルを当てはめる

構文

Mdl = fitrkernel(X,Y)

Mdl = fitrkernel(Tbl,ResponseVarName)

Mdl = fitrkernel(Tbl,formula)

Mdl = fitrkernel(Tbl,Y)

Mdl = fitrkernel(___,Name,Value)

[Mdl,FitInfo] = fitrkernel(___)

[Mdl,FitInfo,HyperparameterOptimizationResults] = fitrkernel(___)

説明

fitrkernel は、非線形回帰用のガウス カーネル回帰モデルの学習または交差検証を行います。fitrkernel は、大規模な学習セットが含まれているビッグ データ事例に使用する方が現実的ですが、メモリに収まる小規模なデータ セットにも適用できます。

fitrkernel は、低次元空間のデータを高次元空間にマッピングしてから、正則化された目的関数を最小化することによって高次元空間で線形モデルを当てはめます。高次元空間で線形モデルを取得することは、低次元空間におけるモデルへのガウス カーネルの適用と等価です。使用可能な線形回帰モデルには、正則化されたサポート ベクター マシン (SVM) と最小二乗回帰モデルがあります。

インメモリ データに対して非線形 SVM 回帰モデルに学習をさせる方法については、fitrsvm を参照してください。

Mdl = fitrkernel(X,Y) は、X 内の予測子データと Y 内の対応する応答を使用して学習をさせたコンパクトなガウス カーネル回帰モデルを返します。

Mdl = fitrkernel(Tbl,ResponseVarName) は、テーブル Tbl に含まれる予測子変数と Tbl.ResponseVarName 内の応答値を使用して学習させたカーネル回帰モデル Mdl を返します。

Mdl = fitrkernel(Tbl,formula) は、テーブル Tbl 内の標本データを使用して学習させたカーネル回帰モデルを返します。入力引数 formula は、Mdl を当てはめるために使用する Tbl 内の予測子変数の応答およびサブセットの説明モデルです。

Mdl = fitrkernel(Tbl,Y) は、テーブル Tbl 内の予測子変数とベクトル Y 内の応答値を使用して、カーネル回帰モデルを返します。

Mdl = fitrkernel(___,Name,Value) では、前の構文におけるいずれかの入力引数の組み合わせに加えて、1 つ以上の名前と値のペアの引数を使用してオプションを指定します。たとえば、最小二乗回帰の実装、拡張空間の次元数の指定、交差検証オプションの指定を行うことができます。

[Mdl,FitInfo] = fitrkernel(___) は、前の構文の入力引数のいずれかを使用して、当てはめの情報も構造体配列 FitInfo に返します。交差検証済みモデルについて FitInfo を要求することはできません。

[Mdl,FitInfo,HyperparameterOptimizationResults] = fitrkernel(___) は、名前と値のペアの引数 'OptimizeHyperparameters' を使用してハイパーパラメーターを最適化する場合に、ハイパーパラメーター最適化の結果も返します。

例

ガウス カーネル回帰モデルの学習

SVM を使用して、tall 配列についてカーネル回帰モデルに学習をさせます。

tall 配列に対する計算を実行する場合、MATLAB® は並列プール (Parallel Computing Toolbox™ がある場合は既定) またはローカルの MATLAB セッションを使用します。Parallel Computing Toolbox がある場合にローカルの MATLAB セッションを使用して例を実行するには、関数 mapreducer を使用してグローバルな実行環境を変更します。

mapreducer(0)

データがあるフォルダーの場所を参照するデータストアを作成します。データは、単一のファイル、ファイルの集まり、またはフォルダー全体のどれに含まれていてもかまいません。datastore によって NaN 値に置き換えられるようにするため、'NA' 値を欠損データとして扱います。使用する変数のサブセットを選択します。データストアの先頭に tall table を作成します。

varnames = {'ArrTime','DepTime','ActualElapsedTime'};
ds = datastore('airlinesmall.csv','TreatAsMissing','NA',...
    'SelectedVariableNames',varnames);
t = tall(ds);

予測子変数 (X) として DepTime と ArrTime を、応答変数 (Y) として ActualElapsedTime を指定します。ArrTime が DepTime より遅い観測値を選択します。

daytime = t.ArrTime>t.DepTime;
Y = t.ActualElapsedTime(daytime);     % Response data
X = t{daytime,{'DepTime' 'ArrTime'}}; % Predictor data

予測子変数を標準化します。

Z = zscore(X); % Standardize the data

標準化された予測子を使用して、既定のガウス カーネル回帰モデルに学習をさせます。当てはめの要約を抽出して、最適化アルゴリズムによりモデルがどの程度適切にデータに当てはめられたかを判断します。

[Mdl,FitInfo] = fitrkernel(Z,Y)

Found 6 chunks.
|=========================================================================
| Solver | Iteration  /  |   Objective   |   Gradient    | Beta relative |
|        | Data Pass     |               |   magnitude   |    change     |
|=========================================================================
|   INIT |     0 /     1 |  4.307833e+01 |  9.925486e-02 |           NaN |
|  LBFGS |     0 /     2 |  2.782790e+01 |  7.202403e-03 |  9.891473e-01 |
|  LBFGS |     1 /     3 |  2.781351e+01 |  1.806211e-02 |  3.220672e-03 |
|  LBFGS |     2 /     4 |  2.777773e+01 |  2.727737e-02 |  9.309939e-03 |
|  LBFGS |     3 /     5 |  2.768591e+01 |  2.951422e-02 |  2.833343e-02 |
|  LBFGS |     4 /     6 |  2.755857e+01 |  5.124144e-02 |  7.935278e-02 |
|  LBFGS |     5 /     7 |  2.738896e+01 |  3.089571e-02 |  4.644920e-02 |
|  LBFGS |     6 /     8 |  2.716704e+01 |  2.552696e-02 |  8.596406e-02 |
|  LBFGS |     7 /     9 |  2.696409e+01 |  3.088621e-02 |  1.263589e-01 |
|  LBFGS |     8 /    10 |  2.676203e+01 |  2.021303e-02 |  1.533927e-01 |
|  LBFGS |     9 /    11 |  2.660322e+01 |  1.221361e-02 |  1.351968e-01 |
|  LBFGS |    10 /    12 |  2.645504e+01 |  1.486501e-02 |  1.175476e-01 |
|  LBFGS |    11 /    13 |  2.631323e+01 |  1.772835e-02 |  1.161909e-01 |
|  LBFGS |    12 /    14 |  2.625264e+01 |  5.837906e-02 |  1.422851e-01 |
|  LBFGS |    13 /    15 |  2.619281e+01 |  1.294441e-02 |  2.966283e-02 |
|  LBFGS |    14 /    16 |  2.618220e+01 |  3.791806e-03 |  9.051274e-03 |
|  LBFGS |    15 /    17 |  2.617989e+01 |  3.689255e-03 |  6.364132e-03 |
|  LBFGS |    16 /    18 |  2.617426e+01 |  4.200232e-03 |  1.213026e-02 |
|  LBFGS |    17 /    19 |  2.615914e+01 |  7.339928e-03 |  2.803348e-02 |
|  LBFGS |    18 /    20 |  2.620704e+01 |  2.298098e-02 |  1.749830e-01 |
|=========================================================================
| Solver | Iteration  /  |   Objective   |   Gradient    | Beta relative |
|        | Data Pass     |               |   magnitude   |    change     |
|=========================================================================
|  LBFGS |    18 /    21 |  2.615554e+01 |  1.164689e-02 |  8.580878e-02 |
|  LBFGS |    19 /    22 |  2.614367e+01 |  3.395507e-03 |  3.938314e-02 |
|  LBFGS |    20 /    23 |  2.614090e+01 |  2.349246e-03 |  1.495049e-02 |
|========================================================================|

Mdl = 
  RegressionKernel
              ResponseName: 'Y'
                   Learner: 'svm'
    NumExpansionDimensions: 64
               KernelScale: 1
                    Lambda: 8.5385e-06
             BoxConstraint: 1
                   Epsilon: 5.9303

FitInfo = struct with fields:
                  Solver: 'LBFGS-tall'
            LossFunction: 'epsiloninsensitive'
                  Lambda: 8.5385e-06
           BetaTolerance: 1.0000e-03
       GradientTolerance: 1.0000e-05
          ObjectiveValue: 26.1409
       GradientMagnitude: 0.0023
    RelativeChangeInBeta: 0.0150
                 FitTime: 56.3717
                 History: [1x1 struct]

Mdl は RegressionKernel モデルです。回帰誤差を調べるには、Mdl と学習データまたは新しいデータを関数 loss に渡すことができます。または、Mdl と新しい予測子データを関数 predict に渡して、新しい観測値の応答を予測することができます。また、Mdl と学習データを関数 resume に渡して学習を続行することもできます。

FitInfo は、最適化情報が格納されている構造体配列です。最適化終了時の結果が満足できるものであるかどうかを判断するには、FitInfo を使用します。

精度を向上させるため、fitrkernel の名前と値のペアの引数を使用して、最適化反復の最大回数 ('IterationLimit') を増やしたり、許容誤差の値 ('BetaTolerance' および 'GradientTolerance') を小さくしたりすることができます。このようにすると、FitInfo の ObjectiveValue や RelativeChangeInBeta などの尺度が向上します。名前と値のペアの引数 'OptimizeHyperparameters' を使用してモデル パラメーターを最適化することもできます。

カーネル回帰モデルの交差検証

carbig データ セットを読み込みます。

load carbig

予測子変数 (X) と応答変数 (Y) を指定します。

X = [Acceleration,Cylinders,Displacement,Horsepower,Weight];
Y = MPG;

配列 X および Y から、それぞれの配列で NaN 値が含まれている行を削除します。NaN 値が含まれている行を削除してからデータを fitrkernel に渡すと、学習が高速化され、メモリ使用量が少なくなります。

R = rmmissing([X Y]); % Data with missing entries removed
X = R(:,1:5); 
Y = R(:,end); 

5 分割の交差検証を使用してカーネル回帰モデルを交差検証します。予測子変数を標準化します。

Mdl = fitrkernel(X,Y,'Kfold',5,'Standardize',true)

Mdl = 
  RegressionPartitionedKernel
    CrossValidatedModel: 'Kernel'
           ResponseName: 'Y'
        NumObservations: 392
                  KFold: 5
              Partition: [1x1 cvpartition]
      ResponseTransform: 'none'

numel(Mdl.Trained)

ans = 5

Mdl は RegressionPartitionedKernel モデルです。fitrkernel は 5 分割交差検証を実施するので、学習分割 (分割内) 観測値に対して学習をさせる 5 個の RegressionKernel モデルが Mdl に格納されます。

各分割の交差検証損失 (平均二乗誤差) を調べます。

kfoldLoss(Mdl,'mode','individual')

ans = 5×1

   13.1983
   14.2686
   23.9162
   21.0763
   24.3975

カーネル回帰の最適化

名前と値の引数 OptimizeHyperparameters を使用して、自動的にハイパーパラメーターを最適化します。

carbig データ セットを読み込みます。

load carbig

予測子変数 (X) と応答変数 (Y) を指定します。

X = [Acceleration,Cylinders,Displacement,Horsepower,Weight];
Y = MPG;

配列 X および Y から、それぞれの配列で NaN 値が含まれている行を削除します。NaN 値が含まれている行を削除してからデータを fitrkernel に渡すと、学習が高速化され、メモリ使用量が少なくなります。

R = rmmissing([X Y]); % Data with missing entries removed
X = R(:,1:5); 
Y = R(:,end); 

自動的なハイパーパラメーター最適化を使用して、5 分割交差検証損失を最小化するハイパーパラメーターを求めます。名前と値の引数 KernelScale、Lambda、Epsilon、および Standardize の最適な値を fitrkernel で求めるため、OptimizeHyperparameters として 'auto' を指定します。再現性を得るために、乱数シードを設定し、'expected-improvement-plus' の獲得関数を使用します。

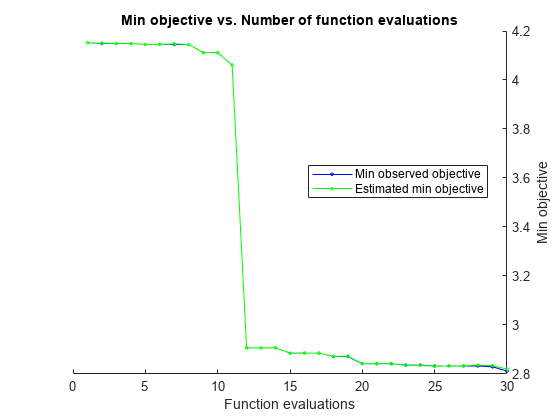
rng('default')
[Mdl,FitInfo,HyperparameterOptimizationResults] = fitrkernel(X,Y,'OptimizeHyperparameters','auto',...
    'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName','expected-improvement-plus'))

|===================================================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |  KernelScale |       Lambda |      Epsilon |  Standardize |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |              |              |
|===================================================================================================================================|
|    1 | Best   |      4.1521 |     0.30569 |      4.1521 |      4.1521 |       11.415 |    0.0017304 |       615.77 |         true |
|    2 | Best   |      4.1489 |     0.11417 |      4.1489 |      4.1503 |       509.07 |    0.0064454 |     0.048411 |         true |
|    3 | Accept |       5.251 |      1.3428 |      4.1489 |      4.1489 |    0.0015621 |   1.8257e-05 |     0.051954 |         true |
|    4 | Accept |      4.3329 |     0.22432 |      4.1489 |      4.1489 |    0.0053278 |         2.37 |       17.883 |        false |
|    5 | Accept |      4.2414 |     0.16841 |      4.1489 |      4.1489 |     0.004474 |      0.13531 |       14.426 |         true |
|    6 | Best   |       4.148 |     0.10239 |       4.148 |       4.148 |      0.43562 |       2.5339 |     0.059928 |         true |
|    7 | Accept |      4.1521 |     0.11964 |       4.148 |       4.148 |       3.2193 |     0.012683 |       813.56 |        false |
|    8 | Best   |      3.8438 |     0.13147 |      3.8438 |      3.8439 |       5.7821 |     0.065897 |        2.056 |         true |
|    9 | Accept |      4.1305 |      0.1233 |      3.8438 |      3.8439 |       110.96 |      0.42454 |       7.6606 |         true |
|   10 | Best   |      3.7951 |     0.12824 |      3.7951 |      3.7954 |       1.1595 |     0.054292 |     0.012493 |         true |
|   11 | Accept |      4.2311 |     0.70699 |      3.7951 |      3.7954 |    0.0011423 |   0.00015862 |       8.6125 |        false |
|   12 | Best   |      2.8871 |      1.3624 |      2.8871 |      2.8872 |       185.22 |   2.1981e-05 |       1.0401 |        false |
|   13 | Accept |      4.1521 |     0.23463 |      2.8871 |      3.0058 |       993.92 |   2.6036e-06 |       58.773 |        false |
|   14 | Best   |      2.8648 |     0.74671 |      2.8648 |      2.8765 |       196.57 |   2.2026e-05 |        1.081 |        false |
|   15 | Accept |      4.2977 |      0.1953 |      2.8648 |      2.8668 |     0.017949 |   1.5685e-05 |        15.01 |        false |
|   16 | Best   |      2.8016 |     0.65159 |      2.8016 |      2.8017 |          786 |   3.4462e-06 |       1.6117 |        false |
|   17 | Accept |      2.9032 |     0.24185 |      2.8016 |      2.8026 |       974.16 |   0.00019486 |       1.6661 |        false |
|   18 | Accept |      2.9051 |      1.6268 |      2.8016 |      2.8018 |       288.21 |   2.6218e-06 |       2.0933 |        false |
|   19 | Accept |      3.4438 |      2.1378 |      2.8016 |       2.803 |       56.999 |    2.885e-06 |       1.3903 |        false |
|   20 | Accept |      2.8436 |      2.1307 |      2.8016 |      2.8032 |       533.99 |   2.7293e-06 |       0.6719 |        false |
|===================================================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |  KernelScale |       Lambda |      Epsilon |  Standardize |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |              |              |
|===================================================================================================================================|
|   21 | Accept |      2.8301 |      1.8305 |      2.8016 |      2.8024 |       411.02 |   3.4347e-06 |      0.98949 |        false |
|   22 | Accept |      2.8233 |     0.60735 |      2.8016 |      2.8043 |       455.25 |   5.2936e-05 |       1.1189 |        false |
|   23 | Accept |      4.1168 |     0.12915 |      2.8016 |       2.802 |       237.02 |      0.85493 |      0.42894 |        false |
|   24 | Best   |      2.7876 |     0.45954 |      2.7876 |      2.7877 |       495.51 |   1.8049e-05 |       1.9006 |        false |
|   25 | Accept |      2.8197 |     0.36807 |      2.7876 |      2.7877 |       927.29 |    1.128e-05 |       1.1902 |        false |
|   26 | Accept |      2.8361 |     0.33532 |      2.7876 |      2.7882 |       354.44 |   6.1939e-05 |       2.2591 |        false |
|   27 | Accept |      2.7985 |     0.46401 |      2.7876 |      2.7906 |       506.54 |   1.4142e-05 |       1.3659 |        false |
|   28 | Accept |      2.8163 |     0.43367 |      2.7876 |      2.7905 |        829.6 |   1.0965e-05 |       2.7415 |        false |
|   29 | Accept |      2.8469 |      1.1727 |      2.7876 |      2.7902 |       729.48 |   3.4914e-06 |     0.039087 |        false |
|   30 | Accept |       2.882 |      1.7445 |      2.7876 |      2.7902 |       255.25 |   3.2869e-06 |     0.059794 |        false |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 32.5757 seconds
Total objective function evaluation time: 20.3399

Best observed feasible point:
    KernelScale      Lambda      Epsilon    Standardize
    ___________    __________    _______    ___________

      495.51       1.8049e-05    1.9006        false   

Observed objective function value = 2.7876
Estimated objective function value = 2.7902
Function evaluation time = 0.45954

Best estimated feasible point (according to models):
    KernelScale      Lambda      Epsilon    Standardize
    ___________    __________    _______    ___________

      495.51       1.8049e-05    1.9006        false   

Estimated objective function value = 2.7902
Estimated function evaluation time = 0.49973

Mdl = 
  RegressionKernel
              ResponseName: 'Y'
                   Learner: 'svm'
    NumExpansionDimensions: 256
               KernelScale: 495.5140
                    Lambda: 1.8049e-05
             BoxConstraint: 141.3376
                   Epsilon: 1.9006

FitInfo = struct with fields:
                  Solver: 'LBFGS-fast'
            LossFunction: 'epsiloninsensitive'
                  Lambda: 1.8049e-05
           BetaTolerance: 1.0000e-04
       GradientTolerance: 1.0000e-06
          ObjectiveValue: 1.3382
       GradientMagnitude: 0.0051
    RelativeChangeInBeta: 9.4332e-05
                 FitTime: 0.1595
                 History: []

HyperparameterOptimizationResults = 
  BayesianOptimization with properties:

                      ObjectiveFcn: @createObjFcn/inMemoryObjFcn
              VariableDescriptions: [6x1 optimizableVariable]
                           Options: [1x1 struct]
                      MinObjective: 2.7876
                   XAtMinObjective: [1x4 table]
             MinEstimatedObjective: 2.7902
          XAtMinEstimatedObjective: [1x4 table]
           NumObjectiveEvaluations: 30
                  TotalElapsedTime: 32.5757
                         NextPoint: [1x4 table]
                            XTrace: [30x4 table]
                    ObjectiveTrace: [30x1 double]
                  ConstraintsTrace: []
                     UserDataTrace: {30x1 cell}
      ObjectiveEvaluationTimeTrace: [30x1 double]
                IterationTimeTrace: [30x1 double]
                        ErrorTrace: [30x1 double]
                  FeasibilityTrace: [30x1 logical]
       FeasibilityProbabilityTrace: [30x1 double]
               IndexOfMinimumTrace: [30x1 double]
             ObjectiveMinimumTrace: [30x1 double]
    EstimatedObjectiveMinimumTrace: [30x1 double]

ビッグ データの場合、最適化手順に時間がかかる可能性があります。最適化手順を実行するにはデータ セットが大きすぎる場合、データの一部だけを使用してパラメーターの最適化を試すことができます。関数 datasample を使用し、'Replace','false' を指定して、データを非復元抽出します。

入力引数

X — 予測子データ

数値行列

回帰モデルを当てはめる対象となる予測子データ。n 行 p 列の数値行列を指定します。n は観測値の個数、p は予測子変数の個数です。

Y の長さと X の観測値数は同じでなければなりません。

データ型: single | double

Y — 応答データ

数値ベクトル

応答データ。n 次元の数値ベクトルを指定します。Y の長さは X または Tbl の観測値の数と等しくなければなりません。

データ型: single | double

Tbl — 標本データ

テーブル

モデルを学習させるために使用する標本データ。テーブルとして指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。オプションとして、Tbl に応答変数用の列を 1 つ追加できます。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

• Tbl に応答変数が含まれている場合に Tbl 内の他の変数をすべて予測子として使用するには、ResponseVarName を使用して応答変数を指定します。

• Tbl に応答変数が含まれている場合に Tbl 内の他の変数の一部のみを予測子として使用するには、formula を使用して式を指定します。

• Tbl に応答変数が含まれていない場合は、Y を使用して応答変数を指定します。応答変数の長さと Tbl の行数は等しくなければなりません。

ResponseVarName — 応答変数名

Tbl 内の変数の名前

応答変数の名前。Tbl 内の変数の名前で指定します。応答変数は、数値ベクトルでなければなりません。

ResponseVarName には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、応答変数 Y が Tbl に Tbl.Y として格納されている場合、'Y' を指定します。それ以外の場合、モデルを学習させるときに、Tbl の列は Y を含めてすべて予測子として扱われます。

データ型: char | string

formula — 応答変数および予測子変数サブセットの説明モデル

文字ベクトル | string スカラー

応答変数および予測子変数サブセットの説明モデル。"Y~x1+x2+x3" という形式の文字ベクトルまたは string スカラーを指定します。この形式では、Y は応答変数を、x1、x2 および x3 は予測子変数を表します。

モデルに学習をさせるための予測子として Tbl 内の変数のサブセットを指定するには、式を使用します。式を指定した場合、formula に現れない Tbl 内の変数は使用されません。

式の変数名は Tbl の変数名 (Tbl.Properties.VariableNames) であり、有効な MATLAB^® 識別子でなければなりません。関数 isvarname を使用して Tbl の変数名を検証できます。変数名が有効でない場合、関数 matlab.lang.makeValidName を使用してそれらを変換できます。

データ型: char | string

メモ

ソフトウェアは、NaN、空の文字ベクトル ('')、空の string ("")、<missing>、および <undefined> の要素を欠損値として扱い、以下のいずれかの特性をもつ観測値を削除します。

• 応答変数の欠損値

• 予測子の観測値 (X または Tbl の行) 内の少なくとも 1 つの欠損値

• 重み ('Weights') が NaN 値または 0

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

例: Mdl = fitrkernel(X,Y,Learner="leastsquares",NumExpansionDimensions=2^15,KernelScale="auto") は、ヒューリスティックな手順により選択されたカーネル スケール パラメーターによる特徴量拡張を使用して、予測子データを 2^15 次元空間にマッピングしてから最小二乗回帰を実施します。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: Mdl = fitrkernel(X,Y,'Learner','leastsquares','NumExpansionDimensions',2^15,'KernelScale','auto')

メモ

交差検証の名前と値の引数は、名前と値の引数 'OptimizeHyperparameters' と一緒には使用できません。'OptimizeHyperparameters' の場合の交差検証は、名前と値の引数 'HyperparameterOptimizationOptions' を使用することのみによって変更できます。

カーネル回帰のオプション

BoxConstraint — ボックス制約

1 (既定値) | 正のスカラー

ボックス制約。'BoxConstraint' と正のスカラーで構成されるコンマ区切りペアとして指定します。

この引数は、'Learner' が 'svm' (既定値) であり、正則化項の強度 'Lambda' の値を指定しなかった場合のみ有効です。ボックス制約 (C) と正則化項の強度 (λ) には C = 1/(λn) という関係があるので、'BoxConstraint' または 'Lambda' のいずれかを指定できます。n は観測値 (X の行) の個数です。

例: 'BoxConstraint',100

データ型: single | double

Epsilon — イプシロン不感応区間の幅の半分

'auto' (既定値) | 非負のスカラー値

イプシロン不感応区間の幅の半分。'Epsilon' と 'auto' または非負のスカラー値から構成されるコンマ区切りのペアとして指定します。

'auto' の場合、関数 fitrkernel は Epsilon の値を iqr(Y)/13.49 に決定します。これは、応答変数 Y の四分位数間範囲を使用した標準偏差の 1/10 の推定値です。iqr(Y) がゼロに等しい場合、fitrkernel は Epsilon の値を 0.1 に設定します。

'Epsilon' は、Learner が svm である場合のみ有効です。

例: 'Epsilon',0.3

データ型: single | double

NumExpansionDimensions — 拡張空間の次元数

'auto' (既定値) | 正の整数

拡張空間の次元数。'NumExpansionDimensions' と 'auto' または正の整数から構成されるコンマ区切りのペアとして指定します。'auto' の場合、関数 fitrkernel は 2.^ceil(min(log2(p)+5,15)) を使用して次元数を選択します。p は予測子の個数です。

例: 'NumExpansionDimensions',2^15

データ型: char | string | single | double

KernelScale — カーネル スケール パラメーター

1 (既定値) | 'auto' | 正のスカラー

カーネル スケール パラメーター。'KernelScale' と 'auto' または正のスカラーから構成されるコンマ区切りのペアとして指定します。MATLAB は、このカーネル スケール パラメーターを使用して、ランダムな特徴量拡張のためのランダムな基底を取得します。詳細については、ランダムな特徴量拡張を参照してください。

'auto' が指定された場合、MATLAB はヒューリスティック手法を使用して適切なカーネル スケール パラメーターを選択します。このヒューリスティック手法では副標本抽出を使用するので、呼び出すたびに推定値が変化する可能性があります。このため、結果を再現するには、学習の前に rng を使用して乱数シードを設定します。

例: 'KernelScale','auto'

データ型: char | string | single | double

Lambda — 正則化項の強度

'auto' (既定値) | 非負のスカラー

正則化項の強度。'Lambda' と 'auto' または非負のスカラーから構成されるコンマ区切りのペアとして指定します。

'auto' の場合、Lambda の値は 1/n です。n は観測値の個数です。

Learner が 'svm' の場合、ボックス制約 (C) と正則化項の強度 (λ) には C = 1/(λn) という関係があるので、BoxConstraint または Lambda のいずれかを指定できます。

例: 'Lambda',0.01

データ型: char | string | single | double

Learner — 線形回帰モデルのタイプ

'svm' (既定値) | 'leastsquares'

線形回帰モデルのタイプ。'Learner' と 'svm' または 'leastsquares' から構成されるコンマ区切りのペアとして指定します。

次の表では $$f\left(x\right)=T(x)\beta +b.$$ です。

• x は p 個の予測子変数による観測値 (行ベクトル) です。

• $$T(·)$$ は特徴量を拡張するための観測値 (行ベクトル) の変換です。T(x) は $${ℝ}^p$$ の x を高次元空間 ($${ℝ}^m$$) にマッピングします。

• β は係数のベクトルです。

• b はスカラー バイアスです。

値	アルゴリズム	応答の範囲	損失関数
'leastsquares'	通常の最小二乗による線形回帰	y ∊ (-∞,∞)	平均二乗誤差 (MSE): $$\ell \left[y,f\left(x\right)\right]=\frac{1}{2}{\left[y-f\left(x\right)\right]}^2$$
'svm'	サポート ベクター マシン回帰	'leastsquares' と同じ	イプシロン不感応: $$\ell \left[y,f\left(x\right)\right]=\max \left[0,\left|y-f\left(x\right)\right|-\epsilon \right]$$

例: 'Learner','leastsquares'

Standardize — 予測子データを標準化するためのフラグ

false または 0 (既定値) | true または 1

R2023b 以降

予測子データを標準化するためのフラグ。数値または logical の 0 (false) または 1 (true) として指定します。Standardize を true に設定すると、各数値予測子変数が対応する列の平均値と標準偏差によってセンタリングおよびスケーリングされます。ソフトウェアは、カテゴリカル予測子を標準化しません。

例: "Standardize",true

データ型: single | double | logical

Verbose — 詳細レベル

0 (既定値) | 1

詳細レベル。'Verbose' と 0 または 1 のいずれかから構成されるコンマ区切りのペアとして指定します。Verbose は、fitrkernel がコマンド ラインに表示する診断情報の量を制御します。

値	説明
0	fitrkernel は診断情報を表示しません。
1	fitrkernel は、目的関数の値や勾配の大きさなどの診断情報を表示および格納します。診断情報は FitInfo.History に格納されます。

例: 'Verbose',1

データ型: single | double

BlockSize — 割り当てられたメモリの最大容量

4e^3 (4 GB) (既定値) | 正のスカラー

割り当てられたメモリの最大容量 (メガバイト)。'BlockSize' と正のスカラーから構成されるコンマ区切りのペアとして指定します。

変換後の予測子データを保持するために fitrkernel で必要となるメモリが BlockSize の値より多い場合、MATLAB はブロック単位方式を使用します。ブロック単位方式の詳細については、アルゴリズムを参照してください。

例: 'BlockSize',1e4

データ型: single | double

RandomStream — 乱数ストリーム

グローバル ストリーム (既定値) | 乱数ストリーム オブジェクト

データ変換の再現性を得るための乱数ストリーム。'RandomStream' と乱数ストリーム オブジェクトから構成されるコンマ区切りのペアとして指定します。詳細については、ランダムな特徴量拡張を参照してください。

X 内のデータを高次元空間に変換するために fitrkernel が使用するランダムな基底関数を再現するには、'RandomStream' を使用します。詳細は、RandStream を使用したグローバル ストリームの管理 と 乱数ストリームの作成と管理 を参照してください。

例: 'RandomStream',RandStream('mlfg6331_64')

他の回帰のオプション

CategoricalPredictors — カテゴリカル予測子のリスト

正の整数のベクトル | logical ベクトル | 文字行列 | string 配列 | 文字ベクトルの cell 配列 | 'all'

カテゴリカル予測子のリスト。次の表のいずれかの値として指定します。

値	説明
正の整数のベクトル	ベクトルの各エントリは、対応する予測子がカテゴリカルであることを示すインデックス値です。インデックス値の範囲は 1 ～ p です。p はモデルの学習に使用した予測子の数です。 fitrkernel が入力変数のサブセットを予測子として使用する場合、関数はサブセットのみを使用して予測子にインデックスを作成します。応答変数、観測値の重みの変数、および関数で使用されないその他の変数は、CategoricalPredictors 値でカウントされません。
logical ベクトル	true というエントリは、対応する予測子がカテゴリカルであることを意味します。ベクトルの長さは p です。
文字行列	行列の各行は予測子変数の名前です。名前は PredictorNames のエントリに一致しなくてはなりません。文字行列の各行が同じ長さになるように、名前を余分な空白で埋めてください。
文字ベクトルの cell 配列または string 配列	配列の各要素は予測子変数の名前です。名前は PredictorNames のエントリに一致しなくてはなりません。
"all"	すべての予測子がカテゴリカルです。

既定では、予測子データがテーブル (Tbl) 内にある場合、fitrkernel は、その変数が logical ベクトル、categorical ベクトル、文字配列、string 配列または文字ベクトルの cell 配列のいずれかである場合に、変数を categorical であると見なします。予測子データが行列 (X) である場合、fitrkernel はすべての予測子が連続的であると見なします。他の予測子をカテゴリカル予測子として指定するには、名前と値の引数 CategoricalPredictors を使用してそれらを指定します。

特定されたカテゴリカル予測子に対して、fitrkernel はカテゴリカル変数に順序が設定されていないか順序が設定されているかに応じて、2 つの異なる方式を使用してダミー変数を作成します。順序付けのないカテゴリカル変数の場合、fitrkernel は、そのカテゴリカル変数の各レベルについて 1 つずつダミー変数を作成します。順序付けされたカテゴリカル変数の場合、fitrkernel は、カテゴリの数よりも 1 つ少ないダミー変数を作成します。詳細については、ダミー変数の自動作成を参照してください。

例: 'CategoricalPredictors','all'

データ型: single | double | logical | char | string | cell

PredictorNames — 予測子変数名

一意な名前の string 配列 | 一意な文字ベクトルの cell 配列

予測子変数名。一意な名前の string 配列または一意な文字ベクトルの cell 配列として指定します。PredictorNames の機能は、学習データの提供方法によって決まります。

• X と Y を指定した場合、PredictorNames を使用して X 内の予測子変数に名前を割り当てることができます。

  • PredictorNames 内の名前の順序は、X の列の順序に一致しなければなりません。つまり、PredictorNames{1} は X(:,1) の名前、PredictorNames{2} は X(:,2) の名前であり、他も同様です。また、size(X,2) と numel(PredictorNames) は等しくなければなりません。

  • 既定では PredictorNames は {'x1','x2',...} です。

• Tbl を指定する場合、PredictorNames を使用して学習に使用する予測子変数を選択できます。つまり、fitrkernel は、学習中に PredictorNames の予測子変数と応答変数のみを使用します。

  • PredictorNames は Tbl.Properties.VariableNames のサブセットでなければならず、応答変数の名前を含めることはできません。

  • 既定では、すべての予測子変数の名前が PredictorNames に格納されます。

  • PredictorNames と formula の両方ではなく、いずれか一方を使用して学習用の予測子を指定することをお勧めします。

例: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]

データ型: string | cell

ResponseName — 応答変数名

"Y" (既定値) | 文字ベクトル | string スカラー

応答変数名。文字ベクトルまたは string スカラーとして指定します。

• Y を指定した場合、ResponseName を使用して応答変数の名前を指定できます。

• ResponseVarName または formula を指定した場合、ResponseName を使用できません。

例: "ResponseName","response"

データ型: char | string

ResponseTransform — 生の応答値を変換するための関数

'none' (既定値) | 関数ハンドル | 関数名

生の応答値を変換するための関数。関数ハンドルまたは関数名として指定します。既定の設定は 'none' です。これは @(y)y、つまり変換なしを表します。関数ハンドルは、ベクトル (元の応答値) を受け入れて同じサイズのベクトル (変換した応答値) を返さなければなりません。

例: myfunction = @(y)exp(y) を使用して、指数変換を入力ベクトルに適用する関数のハンドルを作成するとします。この場合、応答変換として 'ResponseTransform',myfunction を指定できます。

データ型: char | string | function_handle

Weights — 観測値の重み

スカラー値のベクトル | Tbl 内の変数の名前

観測値の重み。'Weights' とスカラー値のベクトルまたは Tbl 内の変数の名前から構成されるコンマ区切りのペアとして指定します。ソフトウェアは、X または Tbl の各観測値 (行) に、Weights の対応する値で重みを付けます。Weights の長さは、X または Tbl の行数と等しくなければなりません。

入力データをテーブル Tbl として指定した場合、Weights は数値ベクトルが含まれている Tbl 内の変数の名前にすることができます。この場合、Weights には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、重みのベクトル W が Tbl.W として格納されている場合、'W' として指定します。それ以外の場合、モデルを学習させるときに、Tbl の列は W を含めてすべて予測子として扱われます。

既定の設定では、Weights は ones(n,1) です。n は X または Tbl の観測値数です。

fitrkernel は合計が 1 になるように重みを正規化します。

データ型: single | double | char | string

交差検証オプション

CrossVal — 交差検証フラグ

'off' (既定値) | 'on'

交差検証フラグ。'Crossval' と 'on' または 'off' から構成されるコンマ区切りのペアとして指定します。

'on' を指定した場合、10 分割の交差検証が実施されます。

名前と値のペアの引数 CVPartition、Holdout、KFold または Leaveout を使用すると、この交差検証の設定を変更できます。交差検証済みモデルを作成するときに使用できる交差検証の名前と値のペアの引数は、一度に 1 つだけです。

例: 'Crossval','on'

CVPartition — 交差検証分割

[] (既定値) | cvpartition オブジェクト

交差検証分割。交差検証のタイプと学習セットおよび検証セットのインデックス付けを指定する cvpartition オブジェクトとして指定します。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: cvp = cvpartition(500,KFold=5) を使用して、500 個の観測値に対する 5 分割交差検証について無作為な分割を作成するとします。この場合、CVPartition=cvp を設定して交差検証分割を指定できます。

Holdout — ホールドアウト検証の対象データの比率

(0,1) の範囲のスカラー値

ホールドアウト検証に使用するデータの比率。範囲 [0,1] のスカラー値として指定します。Holdout=p を指定した場合、以下の手順が実行されます。

1. p*100% のデータを無作為に選択して検証データとして確保し、残りのデータを使用してモデルに学習をさせる。

2. コンパクトな学習済みモデルを交差検証済みモデルの Trained プロパティに格納する。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: Holdout=0.1

データ型: double | single

KFold — 分割の数

10 (既定値) | 1 より大きい正の整数値

交差検証済みモデルで使用する分割の数。1 より大きい正の整数値として指定します。KFold=k を指定した場合、以下の手順が実行されます。

1. データを無作為に k 個のセットに分割する。

2. 各セットについて、そのセットを検証データとして確保し、他の k – 1 個のセットを使用してモデルに学習をさせる。

3. k 個のコンパクトな学習済みモデルを、交差検証済みモデルの Trained プロパティに含まれている k 行 1 列の cell ベクトルに格納する。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: KFold=5

データ型: single | double

Leaveout — Leave-one-out 法の交差検証のフラグ

'off' (既定値) | 'on'

Leave-one-out 法の交差検証のフラグ。'Leaveout' と 'on' または 'off' で構成されるコンマ区切りのペアとして指定します。'Leaveout','on' を指定した場合、n 個の観測値 (n は欠損観測値を除外した観測値の個数) のそれぞれについて以下の手順が実行されます。

1. その観測値を検証データとして確保し、他の n - 1 個の観測値を使用してモデルに学習をさせる。

2. n 個のコンパクトな学習済みモデルを、交差検証済みモデルの Trained プロパティに含まれている n 行 1 列の cell ベクトルのセルに格納する。

交差検証済みモデルの作成に使用できる名前と値のペアの引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: 'Leaveout','on'

収束制御

BetaTolerance — 線形係数およびバイアス項の相対許容誤差

1e-4 (既定値) | 非負のスカラー

線形係数およびバイアス項 (切片) の相対許容誤差。非負のスカラーとして指定します。

$$B_t=\left[{\beta }_t{}^{\prime }{b}_t\right]$$ であるとします。これは、最適化反復 t における係数およびバイアス項のベクトルです。$${\Vert \frac{B_t-B_{t-1}}{B_t}\Vert }_2<\text{BetaTolerance}$$ で最適化が終了します。

GradientTolerance も指定した場合、いずれかの終了条件が満たされると最適化が終了します。

例: 'BetaTolerance',1e-6

データ型: single | double

GradientTolerance — 勾配の絶対許容誤差

1e-6 (既定値) | 非負のスカラー

勾配の絶対許容誤差。非負のスカラーとして指定します。

最適化反復 t における係数およびバイアス項に関する目的関数の勾配ベクトルを $$\nabla {ℒ}_t$$ とします。$${\Vert \nabla {ℒ}_t\Vert }_{\infty }=\max \left|\nabla {ℒ}_t\right|<\text{GradientTolerance}$$ で最適化が終了します。

BetaTolerance も指定した場合、いずれかの終了条件が満たされると最適化が終了します。

例: 'GradientTolerance',1e-5

データ型: single | double

HessianHistorySize — ヘッセ近似の履歴バッファーのサイズ

15 (既定値) | 正の整数

ヘッセ近似の履歴バッファーのサイズ。'HessianHistorySize' と正の整数から構成されるコンマ区切りのペアとして指定します。各反復において、fitrkernel は最新の HessianHistorySize 回の反復の統計量を使用してヘッシアンを構成します。

例: 'HessianHistorySize',10

データ型: single | double

IterationLimit — 最適化反復の最大回数

正の整数

最適化反復の最大回数。'IterationLimit' と正の整数から構成されるコンマ区切りのペアとして指定します。

BlockSize で指定されたメモリに変換後のデータが収まる場合、既定値は 1000 です。それ以外の場合、既定値は 100 です。

例: 'IterationLimit',500

データ型: single | double

ハイパーパラメーター最適化オプション

OptimizeHyperparameters — 最適化するパラメーター

'none' (既定値) | 'auto' | 'all' | 使用可能パラメーター名の string 配列または cell 配列 | optimizableVariable オブジェクトのベクトル

最適化するパラメーター。'OptimizeHyperparameters' と次のいずれかの値から構成されるコンマ区切りのペアとして指定します。

• 'none' — 最適化を行いません。

• 'auto' — {'KernelScale','Lambda','Epsilon','Standardize'} を使用します。

• 'all' — すべての使用可能パラメーターを最適化します。

• 使用可能パラメーター名の cell 配列。

• optimizableVariable オブジェクトのベクトル。通常は hyperparameters の出力です。

最適化では、パラメーターを変化させることにより、fitrkernel の交差検証損失 (誤差) を最小化しようとします。交差検証のタイプおよびその他の最適化の側面を制御するには、名前と値のペアの引数 HyperparameterOptimizationOptions を使用します。

メモ

OptimizeHyperparameters の値は、他の名前と値の引数を使用して指定した値より優先されます。たとえば、OptimizeHyperparameters を "auto" に設定すると、fitrkernel は "auto" オプションに対応するハイパーパラメーターを最適化して、ハイパーパラメーターに指定された値を無視します。

fitrkernel では、以下のパラメーターを使用できます。

• Epsilon — fitrkernel は、既定では範囲 [1e-3,1e2]*iqr(Y)/1.349 の対数スケールで、正の値を探索します。

• KernelScale — fitrkernel は、既定では範囲 [1e-3,1e3] の対数スケールで、正の値を探索します。

• Lambda — fitrkernel は、既定では範囲 [1e-3,1e3]/n の対数スケールで、正の値を探索します。n は観測値の個数です。

• Learner — fitrkernel は 'svm' と 'leastsquares' で探索します。

• NumExpansionDimensions — fitrkernel は、既定では範囲 [100,10000] の対数スケールで、正の整数を探索します。

• Standardize — fitrkernel は、true と false で探索します。

既定以外のパラメーターを設定するには、既定以外の値が含まれている optimizableVariable オブジェクトのベクトルを渡します。以下に例を示します。

load carsmall
params = hyperparameters('fitrkernel',[Horsepower,Weight],MPG);
params(2).Range = [1e-4,1e6];

'OptimizeHyperparameters' の値として params を渡します。

既定では、コマンド ラインに反復表示が表示され、最適化のハイパーパラメーターの個数に従ってプロットが表示されます。最適化とプロットにおける目的関数は、log(1 + cross-validation loss) です。反復表示を制御するには、名前と値の引数 'HyperparameterOptimizationOptions' の Verbose フィールドを設定します。プロットを制御するには、名前と値の引数 'HyperparameterOptimizationOptions' の ShowPlots フィールドを設定します。

たとえば、カーネル回帰の最適化を参照してください。

例: 'OptimizeHyperparameters','auto'

HyperparameterOptimizationOptions — 最適化のオプション

構造体

最適化のオプション。構造体として指定します。この引数を指定すると、名前と値の引数 OptimizeHyperparameters の効果が変化します。この構造体のフィールドは、すべてオプションです。

フィールド名	値	既定の設定
Optimizer	'bayesopt' — ベイズ最適化を使用。内部的には bayesopt が呼び出されます。 'gridsearch' — 次元ごとに NumGridDivisions の値があるグリッド探索を使用。 'randomsearch' — MaxObjectiveEvaluations 個の点で無作為に探索。 'gridsearch' では、グリッドからの一様な非復元抽出により、無作為な順序で探索します。最適化後、sortrows(Mdl.HyperparameterOptimizationResults) コマンドを使用してグリッド順のテーブルを取得できます。	'bayesopt'
AcquisitionFunctionName	'expected-improvement-per-second-plus' 'expected-improvement' 'expected-improvement-plus' 'expected-improvement-per-second' 'lower-confidence-bound' 'probability-of-improvement' オブジェクト関数のランタイムによって最適化が異なるので、名前に per-second が含まれている獲得関数は、再現性がある結果を生成しません。名前に plus が含まれている獲得関数は、領域を過剰利用している場合に動作を変更します。詳細は、獲得関数のタイプを参照してください。	'expected-improvement-per-second-plus'
MaxObjectiveEvaluations	目的関数評価の最大数。	'bayesopt' および 'randomsearch' の場合は 30、'gridsearch' の場合はグリッド全体
MaxTime	制限時間。正の実数スカラーを指定します。制限時間の単位は、tic と toc によって測定される秒です。MaxTime は関数評価を中断させないため、実行時間が MaxTime を超える可能性があります。	Inf
NumGridDivisions	'gridsearch' における各次元の値の個数。値は、各次元の値の個数を表す正の整数のベクトル、またはすべての次元に適用されるスカラーが可能です。カテゴリカル変数の場合、このフィールドは無視されます。	10
ShowPlots	プロットを表示するかどうかを示す論理値。true の場合、最良の観測された目的関数の値が反復回数に対してプロットされます。ベイズ最適化を使用する場合 (Optimizer が 'bayesopt')、最良の推定された目的関数値もプロットされます。最良の観測された目的関数値および最良の推定された目的関数値は、反復表示の BestSoFar (observed) 列および BestSoFar (estim.) 列の値にそれぞれ対応しています。これらの値は、Mdl.HyperparameterOptimizationResults のプロパティ ObjectiveMinimumTrace および EstimatedObjectiveMinimumTrace で確認できます。問題にベイズ最適化の最適化パラメーターが 1 つまたは 2 つある場合、ShowPlots はパラメーターに対する目的関数のモデルもプロットします。	true
SaveIntermediateResults	Optimizer が 'bayesopt' である場合に結果を保存するかどうかを示す論理値。true の場合、'BayesoptResults' という名前のワークスペース変数が反復ごとに上書きされます。この変数は BayesianOptimization オブジェクトです。	false
Verbose	コマンド ラインに次を表示します。 0 — 反復表示なし 1 — 反復表示あり 2 — 追加情報付きで反復表示あり 詳細については、bayesopt の名前と値の引数 Verbose およびベイズ最適化の使用による分類器の当てはめの最適化の例を参照してください。	1
UseParallel	ベイズ最適化を並列実行するかどうかを示す論理値。並列実行には Parallel Computing Toolbox™ が必要です。並列でのタイミングに再現性がないため、並列ベイズ最適化で再現性のある結果が生成されるとは限りません。詳細については、並列ベイズ最適化を参照してください。	false
Repartition	反復ごとに交差検証を再分割するかどうかを示す論理値。false の場合、オプティマイザーは単一の分割を最適化に使用します。 分割ノイズが考慮されるので、通常は true に設定すると最も確実な結果が得られます。ただし、true で良好な結果を得るには、2 倍以上の関数評価が必要になります。	false
以下の 3 つのオプションは 1 つだけ使用できます。
CVPartition	cvpartition によって作成される cvpartition オブジェクト	交差検証フィールドが指定されていない場合 'Kfold',5
Holdout	ホールドアウトの比率を表す範囲 (0,1) のスカラー
Kfold	1 より大きい整数

例: 'HyperparameterOptimizationOptions',struct('MaxObjectiveEvaluations',60)

データ型: struct

出力引数

Mdl — 学習済みのカーネル回帰モデル

RegressionKernel モデル オブジェクト | RegressionPartitionedKernel 交差検証済みモデル オブジェクト

学習済みのカーネル回帰モデル。RegressionKernel モデル オブジェクトまたは RegressionPartitionedKernel 交差検証済みモデル オブジェクトとして返されます。

以下の名前と値のペアの引数のうちいずれかが設定されている場合、Mdl は RegressionPartitionedKernel 交差検証済みモデルとなります。CrossVal、CVPartition、Holdout、KFold または Leaveout。それ以外の場合、Mdl は RegressionKernel モデルです。

Mdl のプロパティを参照するには、ドット表記を使用します。たとえば、拡張空間の次元数を表示するには、コマンド ウィンドウで Mdl.NumExpansionDimensions と入力します。

メモ

他の回帰モデルとは異なり、メモリ消費を節約するため、学習データや学習過程の詳細 (収束履歴など) は RegressionKernel モデル オブジェクトに格納されません。

FitInfo — 最適化の詳細

構造体配列

最適化の詳細。次の表に記載されているフィールドを含む構造体配列として返されます。これらのフィールドには、最終的な値または名前と値のペアの引数の指定が格納されます。

フィールド	説明
Solver	目的関数の最小化手法: 'LBFGS-fast'、'LBFGS-blockwise' または 'LBFGS-tall'。詳細については、アルゴリズムを参照してください。
LossFunction	損失関数。線形回帰モデルのタイプに応じて、平均二乗誤差 (MSE) またはイプシロン不感応になります。Learner を参照してください。
Lambda	正則化項の強度。Lambda を参照してください。
BetaTolerance	線形係数およびバイアス項の相対許容誤差。BetaTolerance を参照してください。
GradientTolerance	勾配の絶対許容誤差。GradientTolerance を参照してください。
ObjectiveValue	最適化終了時の目的関数の値。回帰損失と正則化項を加算することにより目的関数が構成されます。
GradientMagnitude	最適化終了時における目的関数の勾配ベクトルの無限大ノルム。GradientTolerance を参照してください。
RelativeChangeInBeta	最適化終了時の線形係数およびバイアス項の相対的な変化。BetaTolerance を参照してください。
FitTime	モデルをデータに当てはめるためにかかった経過実時間 (秒単位)。
History	最適化情報の履歴。このフィールドには Mdl の学習の最適化情報も格納されます。'Verbose',0 を指定した場合、このフィールドは空 ([]) になります。詳細については、Verbose とアルゴリズムを参照してください。

フィールドにアクセスするには、ドット表記を使用します。たとえば、各反復における目的関数値のベクトルにアクセスするには、コマンド ウィンドウで FitInfo.ObjectiveValue と入力します。

FitInfo が提供する情報を確認して、収束が満足できるものであるかどうかを評価します。

HyperparameterOptimizationResults — ハイパーパラメーターの交差検証最適化

BayesianOptimization オブジェクト | ハイパーパラメーターおよび関連する値のテーブル

ハイパーパラメーターの交差検証最適化。ハイパーパラメーターおよび関連する値が含まれている table または BayesianOptimization オブジェクトとして返されます。'OptimizeHyperparameters' の値が 'none' ではない場合、出力は空以外です。出力値は、名前と値のペアの引数 'HyperparameterOptimizationOptions' の Optimizer フィールドの値に依存します。

Optimizer フィールドの値	HyperparameterOptimizationResults の値
'bayesopt' (既定の設定)	BayesianOptimization クラスのオブジェクト
'gridsearch' または 'randomsearch'	使用したハイパーパラメーター、観測された目的関数の値 (交差検証損失)、および最低 (最良) から最高 (最悪) までの観測値の順位が格納されているテーブル

詳細

ランダムな特徴量拡張

Random Kitchen Sink[1]や Fastfood[2]などのランダムな特徴量拡張は、ビッグ データに対するカーネル回帰アルゴリズムのガウス カーネルを計算効率が高い方法で近似する手法です。ランダムな特徴量拡張は、大規模な学習セットが含まれているビッグ データ事例に対する方が現実的ですが、メモリに収まる小規模なデータ セットにも適用できます。

カーネル回帰アルゴリズムでは、予測子データを高次元空間にマッピングした後で、各応答データ点 (y_i) からの逸脱がイプシロン マージン (ε) の値を超えない最適な関数を求めます。

一部の回帰問題は、線形モデルを使用して適切に表すことはできません。このような場合は、ドット積 x₁x₂′ を非線形カーネル関数 $$G(x_1,x_2)=\langle \phi (x_1),\phi (x_2)\rangle$$ に置き換えることにより非線形回帰モデルを取得します。ここで、x_i は i 番目の観測値 (行ベクトル)、φ(x_i) は x_i を高次元空間にマッピングする変換 ("カーネル トリック" と呼ばれます) です。しかし、(n が大きい) 大規模なデータ セットでは、観測値の各ペアについて G(x₁,x₂) (グラム行列) を評価すると計算コストが高くなります。

ランダムな特徴量拡張の方式では、ドット積がガウス カーネルを近似するようなランダム変換を求めます。つまり、次のようになります。

$$G(x_1,x_2)=\langle \phi (x_1),\phi (x_2)\rangle \approx T(x_1)T(x_2)\text{'},$$

ここで、T(x) は $${ℝ}^p$$ における x を高次元空間 ($${ℝ}^m$$) にマッピングします。Random Kitchen Sink[1]方式では、次のランダムな変換を使用します。

$$T(x)=m^{-1/2}\exp \left(iZx\text{'}\right)\text{'},$$

ここで、$$Z\in {ℝ}^{m\times p}$$ は $$N\left(0,{\sigma }^{-2}\right)$$ から抽出した標本、σ はカーネル スケールです。この方式では O(mp) の計算および格納が必要です。Fastfood[2]方式では、ガウス スケーリング行列と組み合わせたアダマール行列を使用して、Z の代わりに別のランダムな基底 V を導入します。このランダムな基底により、計算コストが O(mlogp) に、ストレージが O(m) に削減されます。

m および σ の値はそれぞれ、fitrkernel の名前と値のペアの引数 NumExpansionDimensions および KernelScale を使用して指定できます。

関数 fitrkernel は、ランダムな特徴量拡張に Fastfood 方式を使用し、線形回帰を使用してガウス カーネル回帰モデルに学習をさせます。関数 fitrsvm のソルバーでは n 行 n 列のグラム行列の計算が必要ですが、fitrkernel のソルバーに必要なのは、n 行 m 列の行列の形成だけです。ビッグ データの場合は一般に m が n よりはるかに小さくなります。

ボックス制約

ボックス制約は、イプシロン マージン (ε) の外部にある観測値に課せられる最大ペナルティを制御するパラメーターであり、過適合の防止 (正則化) に役立ちます。ボックス制約の値を大きくすると、学習時間が長くなる場合があります。

ボックス制約 (C) と正則化項の強度 (λ) には C = 1/(λn) という関係があります。n は観測値の個数です。

ヒント

• モデルに学習させる前に予測子を標準化すると役立つことがあります。

  • 関数 normalize を使用して、学習データを標準化し、テスト データを学習データと同じスケールになるようにスケーリングできます。

  • あるいは、名前と値の引数 Standardize を使用して学習前に数値予測子を標準化します。返されるモデルの Mu プロパティと Sigma プロパティに、予測子の平均と標準偏差がそれぞれ含まれます。 (R2023b 以降)

• モデルに学習をさせた後で、新しいデータについて応答を予測する C/C++ コードを生成できます。C/C++ コードの生成には MATLAB Coder™ が必要です。詳細については、コード生成の紹介を参照してください。

アルゴリズム

fitrkernel は、メモリ制限 Broyden-Fletcher-Goldfarb-Shanno (LBFGS) ソルバーとリッジ (L₂) 正則化を使用して、正則化された目的関数を最小化します。学習に使用した LBFGS ソルバーのタイプを調べるには、コマンド ウィンドウで FitInfo.Solver と入力します。

• 'LBFGS-fast' — LBFGS ソルバー。

• 'LBFGS-blockwise' — ブロック単位方式を使用する LBFGS ソルバー。変換後の予測子データを保持するために fitrkernel で必要となるメモリが BlockSize の値より多い場合、この関数はブロック単位方式を使用します。

• 'LBFGS-tall' — ブロック単位方式の tall 配列用 LBFGS ソルバー。

fitrkernel がブロック単位方式を使用する場合、各反復で損失と勾配の計算をデータのさまざまな部分に分散させることにより LBFGS が実装されます。また、fitrkernel は、データの一部に対して局所的にモデルを当てはめ、平均化で係数を結合することにより、線形係数およびバイアス項の初期推定値を改善します。'Verbose',1 が指定された場合、fitrkernel は各データ通過についての診断情報を表示し、情報を FitInfo の History フィールドに格納します。

fitrkernel がブロック単位方式を使用しない場合、初期推定値はゼロになります。'Verbose',1 が指定された場合、fitrkernel は各反復についての診断情報を表示し、情報を FitInfo の History フィールドに格納します。

参照

[1] Rahimi, A., and B. Recht. “Random Features for Large-Scale Kernel Machines.” Advances in Neural Information Processing Systems. Vol. 20, 2008, pp. 1177–1184.

[2] Le, Q., T. Sarlós, and A. Smola. “Fastfood — Approximating Kernel Expansions in Loglinear Time.” Proceedings of the 30th International Conference on Machine Learning. Vol. 28, No. 3, 2013, pp. 244–252.

[3] Huang, P. S., H. Avron, T. N. Sainath, V. Sindhwani, and B. Ramabhadran. “Kernel methods match Deep Neural Networks on TIMIT.” 2014 IEEE International Conference on Acoustics, Speech and Signal Processing. 2014, pp. 205–209.

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

使用上の注意事項および制限事項:

• fitrkernel は tall table データをサポートしていません。

• 一部の名前と値のペアの引数は、インメモリの関数 fitrkernel と既定値が異なります。サポートされる名前と値のペアの引数および違いは次のとおりです。

  • 'BoxConstraint'

  • 'Epsilon'

  • 'NumExpansionDimensions'

  • 'KernelScale'

  • 'Lambda'

  • 'Learner'

  • 'Verbose' — 既定値は 1 です。

  • 'BlockSize'

  • 'RandomStream'

  • 'ResponseTransform'

  • 'Weights' — 値は tall 配列でなければなりません。

  • 'BetaTolerance' — 既定値は 1e–3 に緩和されます。

  • 'GradientTolerance' — 既定値は 1e–5 に緩和されます。

  • 'HessianHistorySize'

  • 'IterationLimit' — 既定値は 20 に緩和されます。

  • 'OptimizeHyperparameters'

  • 'HyperparameterOptimizationOptions' — 交差検証として、tall 最適化では 'Holdout' 検証のみがサポートされます。既定では、データの 20% がホールドアウト検証データとして選択されて確保され、残りのデータがモデルの学習に使用されます。この引数を使用してホールドアウトの比率に別の値を指定できます。たとえば、データの 30% を検証データとして確保するには 'HyperparameterOptimizationOptions',struct('Holdout',0.3) と指定します。

• 'KernelScale' が 'auto' である場合、fitrkernel は tallrng によって制御される乱数ストリームをサブサンプリングに使用します。再現性を得るには、tallrng によって制御される乱数ストリームとグローバル ストリームの両方について乱数のシードを設定しなければなりません。

• 'Lambda' が 'auto' である場合、fitrkernel は X 内の観測値の個数を計算するため、さらにデータを通過する可能性があります。

• fitrkernel はブロック単位方式を使用します。詳細については、アルゴリズムを参照してください。

詳細は、tall 配列を参照してください。

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

ハイパーパラメーターの最適化を並列実行するには、関数 fitrkernel を呼び出すときに名前と値の引数 'HyperparameterOptimizationOptions', struct('UseParallel',true) を指定します。

並列的なハイパーパラメーターの最適化の詳細については、並列ベイズ最適化を参照してください。

並列計算の全般的な情報については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2018a で導入

R2023b: カーネル モデルで予測子の標準化をサポート

R2023b 以降では、fitrkernel で数値予測子の標準化がサポートされます。つまり、Standardize の値を true として指定することで、各数値予測子変数を対応する列の平均と標準偏差でセンタリングおよびスケーリングできます。ソフトウェアは、カテゴリカル予測子を標準化しません。

名前と値の引数 OptimizeHyperparameters を使用して Standardize ハイパーパラメーターを最適化することもできます。以前のリリースとは異なり、OptimizeHyperparameters の値として "auto" を指定すると、fitrkernel には最適化可能なハイパーパラメーターとして Standardize が含まれます。

参考

bayesopt | bestPoint | fitrlinear | fitrsvm | loss | predict | RegressionKernel | resume | RegressionPartitionedKernel

トピック

• 回帰学習器アプリを使用したカーネル近似モデルの学習
• サポート ベクター マシン回帰について