MATLAB での点群 SLAM の実装
"点群" とは、3 次元空間における点の集合です。点群は、通常、LIDAR や Kinect® デバイスなどの 3 次元スキャナーから取得されます。点群はロボットの操縦および認識、深度推定、ステレオ ビジョン、視覚レジストレーション、および先進運転者支援システム (ADAS) といった分野に応用されています。
"点群のレジストレーション" とは、同じシーンの 2 つ以上の 3 次元点群の位置を合わせて、共通の座標系にするプロセスです。"マッピング" は、ロボットまたはセンサーの周囲の環境のマップを作成するプロセスです。レジストレーションと地図作成を使用して、位置推定のために 3 次元シーンの再構成や道路マップの作成ができます。通常、レジストレーションは地図作成の前に行いますが、変形するものを追跡するなど、地図作成を必要としないレジストレーションの適用もいくつかあります。Computer Vision Toolbox™ アルゴリズムは、点群のレジストレーションと地図作成を実行する関数を提供します。ワークフローは、前処理、レジストレーション、ドリフト補正、および点群の位置合わせで構成されます。
自己位置推定と環境地図作成の同時実行 (SLAM) とは、環境地図作成を行うのと同時に、周囲に対する車両の位置と向きを計算する処理を意味します。この処理では、センサーからの点群入力のみを使用します。点群 SLAM の用途には、ロボティクスや自動運転があります。SLAM が重要である理由や、さまざまな用途での SLAM の応用例の全般的な説明については、SLAM とはを参照してください。
地図作成と位置推定のワークフロー
次の手順に従って、点群のレジストレーションと、一連の点群での地図作成を実行します。次に、事前作成したマップで車両を位置推定できます。
点群の前処理 — レジストレーションのために点群を準備するには、ダウンサンプリングして、不要な特徴とノイズを削除します。
点群のレジストレーション — 各点群をその前の点群に対してレジストレーションします。これらのレジストレーションは、"オドメトリ" で使用されます。これは、連続するフレーム全体のレジストレーション推定を累積するプロセスです。オドメトリを単独で使用すると、測定された姿勢とグラウンド トゥルースの姿勢の間でドリフトが発生する可能性があります。
ループの検出 — ドリフトを最小限に抑えるためにループ閉じ込み検出を実行します。"ループ閉じ込み検出" は、過去にアクセスしたことのある位置へのセンサーの回帰を特定するプロセスであり、センサーの軌道にループを形成します。
ドリフトの修正 — 検出されたループを使用し、"姿勢グラフの最適化" によってドリフトを最小化します。これには、ノードとエッジを追加して姿勢グラフをインクリメンタルに構築し、十分なループが見つかったら姿勢グラフを最適化することが含まれます。姿勢グラフの最適化により、最適化された絶対姿勢のセットが得られます。
マップの組み立て — 最適化された絶対姿勢を使用して、レジストレーションされた点群を位置合わせすることにより、点群マップを組み立てます。このような事前作成した点群マップは、マップ内で車両を見つけるプロセスである "位置推定" に使用できます。
位置推定 — 組み立てられたマップに基づいて車両の姿勢を求めます。
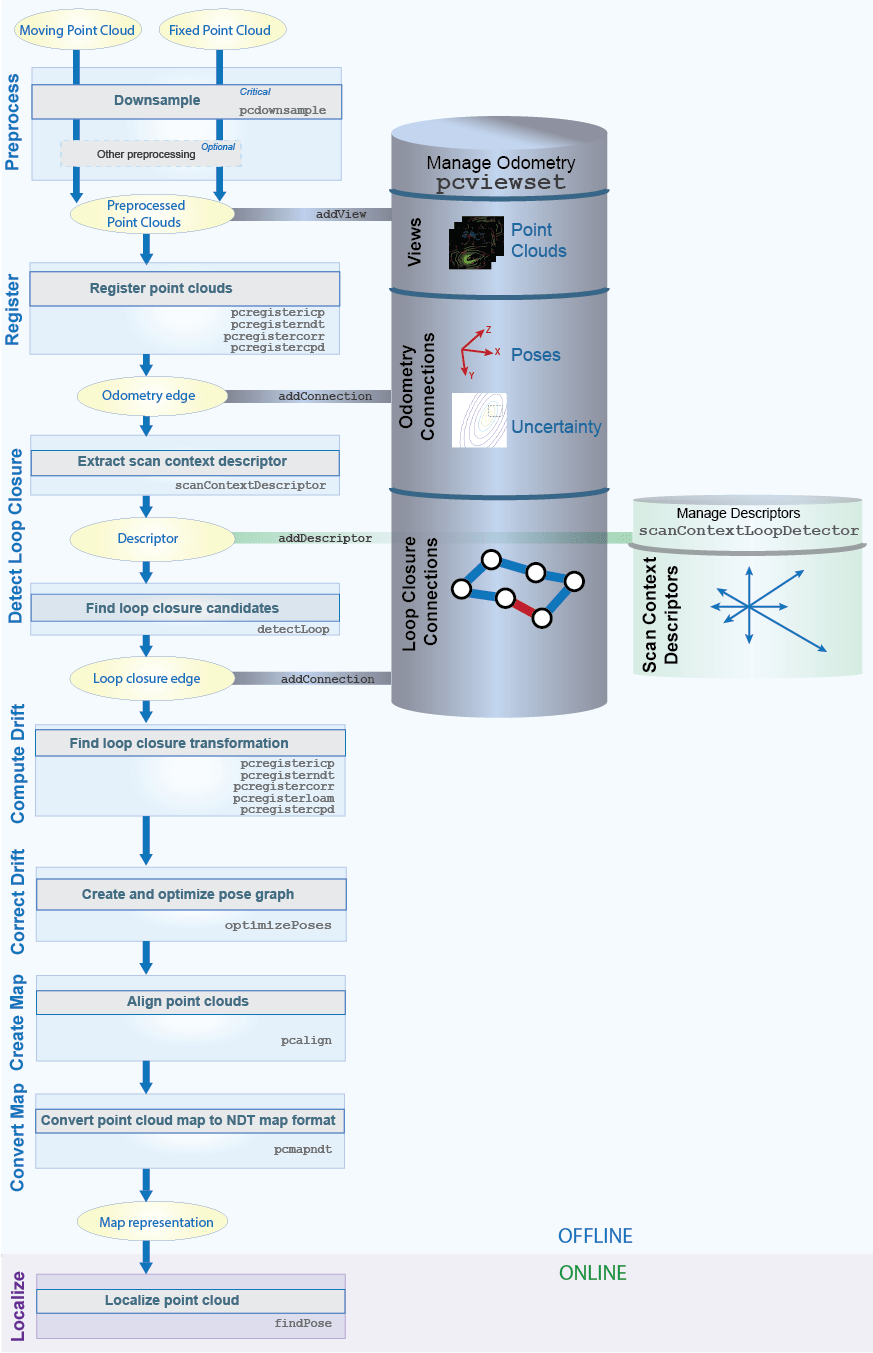
地図作成と位置推定のためのデータの管理
点群のレジストレーションと地図作成のワークフローに関連するデータを管理するために、次のオブジェクトを使用します。
pointCloudオブジェクト — 点群オブジェクトは、3 次元空間に配置された点のセットを格納します。効率的なインデックス作成手法を使用して、最近傍検索を実行します。これは点群の前処理とレジストレーション関数で利用されます。rigidtform3dオブジェクト — 剛体 3 次元オブジェクトは、3 次元剛体幾何学的変換を格納します。このワークフローでは、相対姿勢と絶対姿勢を表します。pcviewsetオブジェクト — 点群ビュー セット オブジェクトは、オドメトリと地図作成プロセスに関連するデータを管理します。一連のビューおよびビュー間のペアワイズ接続としてデータを整理します。また、姿勢グラフを作成および更新します。各 "ビュー" は、点群とそれに関連する絶対姿勢の変換で構成されます。各ビューには、ビュー セット内に一意の識別子があり、姿勢グラフのノードを形成します。
各 "接続" には、あるビューを別のビューに結び付ける情報が格納されます。これには、接続されたビュー間の相対的な変換と、測定の計算に伴う不確実性が含まれます。各接続は、姿勢グラフのエッジを形成します。
scanContextLoopDetectorオブジェクト — ループ閉じ込み検出オブジェクトは、対応するビュー ID とともにスキャン コンテキスト記述子を格納します。ID は、検出されたループ閉じ込みをpcviewsetのビューに関連付けます。pcmapndtオブジェクト — NDT マップ オブジェクトは、圧縮されたメモリ効率の高い地図表現を位置推定用に格納します。オブジェクトは、点群マップをボクセル (3 次元ボックス) のセットに変換します。各ボクセルは 3 次元の正規分布で表されます。
点群の前処理
前処理には、点群から不要な特徴やノイズを削除することや、セグメント化やダウンサンプリングすることが含まれます。前処理には、次の関数を含めることができます。
pcdownsample— 点群をダウンサンプリングします。pcsegdistまたはsegmentLidarData— 点群データをクラスターにセグメント化し、関数selectを使用して目的の点を選択します。pcfitplane、segmentGroundFromLidarData、またはsegmentGroundSMRF(Lidar Toolbox) — グランド プレーンをセグメント化し、関数selectを使用して目的の点を選択します。pcdenoise— 点群から不要なノイズを削除します。
点群のレジストレーション
関数 pcregisterndt、pcregistericp、pcregistercorr、pcregisterloam (Lidar Toolbox)、または pcregistercpd を使用して、移動点群を固定点群にレジストレーションすることができます。これらの関数で使用されているレジストレーション アルゴリズムは、それぞれ正規分布変換 (NDT) アルゴリズム、反復最近接点 (ICP) アルゴリズム、位相相関アルゴリズム、lidar odometry and mapping (LOAM) アルゴリズム、およびコヒーレント点ドリフト (CPD) アルゴリズムに基づいています。これらのアルゴリズムの詳細については、参考文献を参照してください。
点群のレジストレーションを行う際には、シーン内のオブジェクトが固定点群と移動点群の間でどのように変化するかを表す変換のタイプを選択できます。
| 変換 | 説明 |
|---|---|
| 剛体 | 剛体変換は、シーン内のオブジェクトの形状とサイズを保持します。シーン内のオブジェクトには、平行移動、回転、またはその両方を実行できます。同じ変換がすべての点に適用されます。 |
| アフィン | アフィン変換では、オブジェクトの平行移動と回転に加え、せん断とスケール変更が可能です。 |
| 非剛体 | 非剛体変換では、シーン内のオブジェクトの形状を変更できます。点は個別に変換されます。変位場は変換を表します。 |
次の表では、点群レジストレーション関数の選択肢と、それぞれの変換タイプおよびパフォーマンス特性を比較しています。この表を使用して、ユース ケースに適したレジストレーション関数を選択できます。
| レジストレーション手法 (関数) | 変換タイプ | 説明 | パフォーマンス特性 |
|---|---|---|---|
pcregisterndt | 剛体 |
| アルゴリズムがより速く収束できるように、初期推定値を提供する。 |
pcregistericp | 剛体 |
| |
pcregistercorr | 剛体 |
| 占有グリッドのサイズが小さくなり、関数の計算要件が縮小する。 |
pcregisterloam (Lidar Toolbox) | 剛体 |
| 処理速度とレジストレーション精度の間の制御を強化する
|
pcregisterfgr (Lidar Toolbox) | 剛体 |
|
|
pcregistercpd | 剛体、アフィン、および非剛体 |
| 最も低速なレジストレーション手法。マップの作成には非推奨。 |
現在の (移動) 点群を前の (固定) 点群に対してレジストレーションを行うと、固定点群のフレーム内における移動点群の推定相対姿勢を表す rigidtform3d 変換が返されます。この相対姿勢変換を以前に蓄積されたすべての相対姿勢変換で構成すると、絶対姿勢変換の推定が得られます。
移動点群とその絶対姿勢変換によって形成されるビューをビュー セットに追加します。関数 addView を使用して、ビューを pcviewset オブジェクトに追加できます。
関数 addConnection を使用して、"オドメトリ エッジ" を pcviewset オブジェクトに追加します。オドメトリ エッジは、連続するビュー間の接続によって定義されるエッジで、固定点群と移動点群の間の相対姿勢変換によって形成されます。
レジストレーションのヒント
NDT または ICP を使用するようなローカル レジストレーション手法 (それぞれ
pcregisterndtまたはpcregistericp) では、パフォーマンスを向上させるために初期推定値が必要です。初期推定値を取得するには、慣性計測ユニット (IMU) などの別のセンサーや、他の形式のオドメトリを使用します。レジストレーション結果の精度を上げるには、
'MaxIterations'引数の値を増やすか、'Tolerance'引数の値を減らします。上記のようにこれらの値を変更すると、結果的にレジストレーションの速度は遅くなります。レジストレーションの効率と精度を向上させるには、
pcregisterndt、pcregistericp、またはpcregistercpdを使用する前に、pcdownsampleを使って点群のダウンサンプリングを行うことを検討してください。レジストレーションの前に
pcdenoiseを使用してノイズを除去するとレジストレーションの精度が向上しますが、マップ作成ワークフローの実行時間が長くなる可能性があります。
ループの検出
オドメトリを単独で使用すると、誤差の累積によるドリフトが発生します。これらの誤差は、長距離において深刻な不正確さをもたらす可能性があります。グラフベースの自己位置推定と環境地図作成の同時実行 (SLAM) を使用すると、ドリフトが修正されます。これを行うために、記述子マッチングを使用して、前の点群でアクセスした位置を見つけることにより、ループ閉じ込みを検出します。ループ閉じ込みを使用して、蓄積されたドリフトを修正します。ループ閉じ込みを検出するには、次の手順に従います。
関数
scanContextDescriptorを使用して、点群の特徴を取得するスキャン コンテキスト記述子を抽出します。addDescriptorを使用して、スキャン コンテキスト記述子をscanContextLoopDetectorに追加します。関数
detectLoopを使用して、潜在的なループ閉じ込みを見つけます。点群のレジストレーションを行い、ビュー間の相対姿勢変換と、位置合わせされた点群間のユークリッド距離の平方根平均二乗誤差 (RMSE) を決定します。RMSE を使用して、無効なループ閉じ込みをフィルター処理します。相対姿勢変換は、2 つのビュー間の接続を表します。連続しないビュー間の接続によって形成されるエッジは、"ループ閉じ込み エッジ" と呼ばれます。関数
addConnectionを使用して、pcviewsetオブジェクトに接続を追加できます。
セグメント マッチングに基づくループ閉じ込み検出の代替アプローチについては、関数 findPose (Lidar Toolbox) を参照してください。
ドリフトの修正
pcviewset オブジェクトは、ビューと接続が追加されると、姿勢グラフを内部的に更新します。ドリフトを最小限に抑えるために、十分なループ閉じ込みが検出されたら、関数 optimizePoses を使用して姿勢グラフの最適化を実行します。関数 optimizePoses は、ビューごとに最適化された絶対姿勢変換をもつ pcviewset オブジェクトを返します。
関数 createPoseGraph を使用して、姿勢グラフを MATLAB® digraph オブジェクトとして返すことができます。MATLAB のグラフ アルゴリズムを使用して、姿勢グラフを検査、表示、または変更できます。関数 optimizePoseGraph (Navigation Toolbox) を使用して変更された姿勢グラフを最適化し、関数 updateView を使用してビュー セット内の姿勢を更新します。
マップの組み立て
関数 pcalign を使用して、ビュー セットからの点群とそれらの最適化された絶対姿勢変換を使用して点群マップを作成します。この点群マップを使用して、NDT 位置推定アルゴリズムを使用したオンライン位置推定を行うことができます。
マップ内での車両の位置推定
pcmapndt オブジェクトを使用して、事前作成した点群マップを NDT マップ形式に変換します。pcmapndt オブジェクトは、圧縮ボクセル表現でマップを保存します。このマップは、ディスクに保存してオンライン位置推定に使用できます。関数 findPose を使用してマップ内で位置を推定します。
代替ワークフロー
地図構築と位置推定の代替ワークフローは、Computer Vision Toolbox、Navigation Toolbox™、および Lidar Toolbox™ で使用可能です。
Computer Vision Toolbox の機能を使用した Visual SLAM — 環境地図作成を行うのと同時に、周囲に対するカメラの位置と向きを計算します。詳細については、MATLAB での Visual SLAM の実装を参照してください。
Navigation Toolbox の機能を使用した占有マップの作成 — 点群から占有マップを作成します。詳細については、3 次元 LiDAR 点群を使用した SLAM の実行 (Navigation Toolbox)を参照してください。
Lidar Toolbox の機能を使用したセグメント マッチング —
pcmapsegmatch(Lidar Toolbox) オブジェクトを使用してセグメントと特徴の地図表現を作成します。関数findPose(Lidar Toolbox) を使用して、ループ閉じ込みの検出と位置推定を行います。この方法は動的な障害物に対してロバストであり、大規模な環境に推奨されます。この方法の例については、Build Map and Localize Using Segment Matching (Lidar Toolbox)の例を参照してください。以下の表は、pcmapndt地図表現とpcmapsegmatch(Lidar Toolbox) 地図表現の類似点と相違点を示しています。ワークフロー pcmapndtpcmapsegmatchアルゴリズム 正規分布変換 (NDT) SegMatch — セグメント マッチング手法 マッピング 最初にマップを作成 — pcviewsetを使用してインクリメンタルにマップを作成します。次に、pcalignを使用して地図を組み立て、事前作成したマップを NDT 地図表現に変換します。pcmapsegmatch(Lidar Toolbox) を使用してインクリメンタルにマップを作成 — 点群スキャンごとに、pcviewset(addViewを使用) とpcmapsegmatch(Lidar Toolbox) (addView(Lidar Toolbox) を使用) にビューを追加します。findPose(Lidar Toolbox) を使用してループ閉じ込みを検出し、optimizePosesを使用して累積ドリフトを修正します。位置推定の類似点 位置推定用のサブマップを選択し、次のいずれかのオプション セットを使用して位置推定用の姿勢を求めます。
pcmapndtオブジェクトの関数selectSubmapおよび関数findPose。pcmapsegmatch(Lidar Toolbox) オブジェクトの関数selectSubmap(Lidar Toolbox) および関数findPose(Lidar Toolbox)。
位置推定の相違点 姿勢の推定値に依存します。 姿勢の推定値に依存しません。 可視化 pcmapndtオブジェクトの関数showまたはpcmapsegmatch(Lidar Toolbox) オブジェクトの関数show(Lidar Toolbox) を使用して、マップまたは選択したサブマップを可視化します。
参照
[1] Myronenko, Andriy, and Xubo Song. “Point Set Registration: Coherent Point Drift.” IEEE Transactions on Pattern Analysis and Machine Intelligence 32, no. 12 (December 2010): 2262–75. https://doi.org/10.1109/TPAMI.2010.46
[2] Chen, Yang, and Gérard Medioni. “Object Modelling by Registration of Multiple Range Images.” Image and Vision Computing 10, no. 3 (April 1992): 145–55. https://doi.org/10.1016/0262-8856(92)90066-C.
[3] Besl, P.J., and Neil D. McKay. “A Method for Registration of 3-D Shapes.” IEEE Transactions on Pattern Analysis and Machine Intelligence 14, no. 2 (February 1992): 239–56. https://doi.org/10.1109/34.121791.
[4] Biber, P., and W. Strasser. “The Normal Distributions Transform: A New Approach to Laser Scan Matching.” In Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), 3:2743–48. Las Vegas, Nevada, USA: IEEE, 2003. https://doi.org/10.1109/IROS.2003.1249285.
[5] Magnusson, Martin. “The Three-Dimensional Normal-Distributions Transform: An Efficient Representation for Registration, Surface Analysis, and Loop Detection.” PhD thesis, Örebro universitet, 2009.
[6] Dimitrievski, Martin, David Van Hamme, Peter Veelaert, and Wilfried Philips. “Robust Matching of Occupancy Maps for Odometry in Autonomous Vehicles.” In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, 626–33. Rome, Italy: SCITEPRESS - Science and Technology Publications, 2016. https://doi.org/10.5220/0005719006260633.
[7] Zhang, Ji, and Sanjiv Singh. “LOAM: Lidar Odometry and Mapping in Real-Time.” In Robotics: Science and Systems X. Robotics: Science and Systems Foundation, 2014. https://doi.org/10.15607/RSS.2014.X.007.
参考
関数
pcregistercorr|pcregisterndt|pcregistericp|pcregistercpd|pcalign|scanContextDistance|scanContextDescriptor|findPose|show|segmentGroundSMRF(Lidar Toolbox)
オブジェクト
トピック
- SLAM とは
- オーガナイズド点群とアンオーガナイズド点群とは (Lidar Toolbox)
- SLAM を使用した LiDAR データからのマップの作成
- MATLAB での Visual SLAM の実装
- Design Lidar SLAM Algorithm Using Unreal Engine Simulation Environment (Automated Driving Toolbox)
- 3 次元点群のレジストレーションと繋ぎ合わせ
- LiDAR データからのマップの作成
- Build Map and Localize Using Segment Matching (Lidar Toolbox)