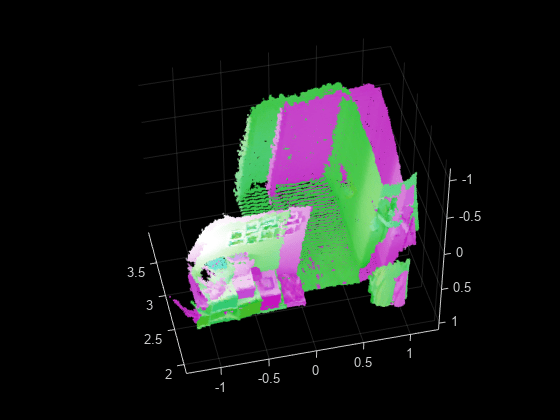
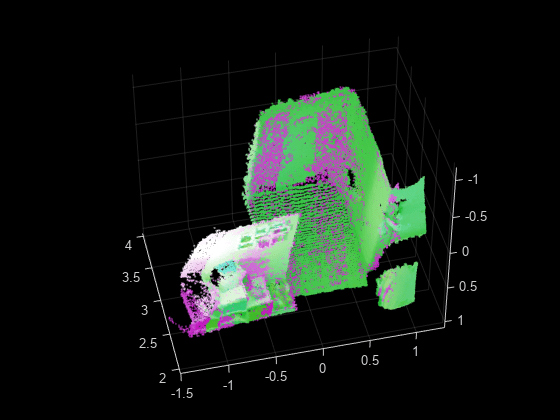
pcregistericp
ICP アルゴリズムを使用した 2 つの点群のレジストレーション
構文
説明
tform = pcregistericp(moving,fixed)
レジストレーション アルゴリズムは反復最近接点 (ICP) アルゴリズムに基づいています。この反復処理で最良のパフォーマンスを得るには、データのプロパティを調整しなければなりません。レジストレーションの精度と効率を向上させるには、pcregistericp を使用する前に pcdownsample を使用して点群をダウンサンプリングすることを検討してください。
"pointToPlane" または "planeToPlane" (Generalized-ICP または G-ICP とも呼ばれる) メトリクスを選択する場合、レジストレーション アルゴリズムには点群の法線が必要です。入力点群の Normal プロパティが空の場合、関数がそれを指定します。
[___] = pcregistericp( は、前の構文にある引数の任意の組み合わせに加えて、名前と値の引数を 1 つ以上使用してオプションを指定します。たとえば、moving,fixed,Name=Value)pcregistericp(moving,fixed,Metric="planeToPlane") は、最小化メトリクスを "planeToPlane" に設定します。
例
点群データをワークスペースに読み込みます。
ptCloud = pcread("teapot.ply");読み込まれた点群を表示します。
pcshow(ptCloud)
title("Teapot")
Z 軸に沿って 30 度回転し、[5 5 10] の並進を行う変換オブジェクトを作成します。
rotationAngles = [0 0 30]; translation = [5 5 10]; tform1 = rigidtform3d(rotationAngles,translation);
点群を変換し、結果を可視化します。
ptCloudTformed = pctransform(ptCloud,tform1);
pcshow(ptCloudTformed)
title("Transformed Teapot")
点群をレジストレーションします。
tform = pcregistericp(ptCloudTformed,ptCloud);
結果を真の変換と比較します。
disp(tform1.A);
0.8660 -0.5000 0 5.0000
0.5000 0.8660 0 5.0000
0 0 1.0000 10.0000
0 0 0 1.0000
tform2 = invert(tform); disp(tform2.A);
0.8660 -0.5000 0.0000 5.0000
0.5000 0.8660 0.0000 5.0000
-0.0000 -0.0000 1.0000 10.0000
0 0 0 1.0000
点群データをワークスペースに読み込みます。
ld = load("livingRoom.mat");
moving = ld.livingRoomData{1};
fixed = ld.livingRoomData{2};点群を可視化し、y 軸を表示する方向を設定します。
figure pcshowpair(moving,fixed,VerticalAxis="Y",VerticalAxisDir="Down")
nonuniformGridSample 法を使用して点群をダウンサンプリングし、レジストレーションの効率と精度を向上させます。
maxNumPoints = 12; fixedDownsampled = pcdownsample(fixed,"nonuniformGridSample",maxNumPoints); movingDownsampled = pcdownsample(moving,"nonuniformGridSample",maxNumPoints);
plane-to-plane (Generalized-ICP) レジストレーションを使用して点群を整列させます。
[~,movingReg] = pcregistericp(movingDownsampled,fixedDownsampled,Metric="planeToPlane");点群の整列を可視化し、y 軸を表示する方向を設定します。
figure pcshowpair(movingReg,fixed,VerticalAxis="Y",VerticalAxisDir="Down")
色情報をもつ移動点群データをワークスペースに読み込みます。
moving = pcread("apartmentMoving.pcd");色情報をもつ固定点群データをワークスペースに読み込みます。
fixed = pcread("apartmentFixed.pcd");色付きの点群を可視化し、yx 平面を表示する方向を設定します。
figure pcshowpair(moving,fixed,"ViewPlane","YX","ColorSource","Color")
plane-to-plane (Generalized-ICP) レジストレーションと色情報を使用して色付きの点群を整列させます。引数 Metric の値を planeToPlaneWithColor として設定します。
[~,movingReg] = pcregistericp(moving,fixed,Metric="planeToPlaneWithColor");点群の整列を可視化し、yx 平面を表示する方向を設定します。
figure pcshowpair(movingReg,fixed,"ViewPlane","YX","ColorSource","Color")
入力引数
名前と値の引数
出力引数
アルゴリズム
参照
[1] Besl, P.J., and Neil D. McKay. “A Method for Registration of 3-D Shapes.” IEEE Transactions on Pattern Analysis and Machine Intelligence 14, no. 2 (February 1992): 239–256. https://doi.org/10.1109/34.121791.
[2] Chen, Yang, and Gérard Medioni. “Object Modelling by Registration of Multiple Range Images.” Image and Vision Computing 10, no. 3 (April 1992): 145–155. https://doi.org/10.1016/0262-8856(92)90066-C.
[3] Segal, A., Haehnel, D. and S. Thrun. "Generalized-ICP". Robotics: Science and Systems V, Robotics: Science and Systems Foundation,. (June 2009): 435-442. https://doi.org/10.15607/RSS.2009.V.021.
[4] Korn, Michael, Martin Holzkothen, and Josef Pauli. "Color supported generalized-ICP." In 2014 International Conference on Computer Vision Theory and Applications (VISAPP), 592–599. Lisbon, Portugal: IEEE, 2014. https://doi.org/10.5220/0004692805920599.
[5] Park, Jaesik, Qian-Yi Zhou, and Vladlen Koltun. "Colored point cloud registration revisited." In Proceedings of the IEEE International Conference on Computer Vision (ICCV), 143-152. Venice, Italy: IEEE, 2017. htttps://doi.org/10.1109/ICCV.2017.25.
拡張機能
バージョン履歴
R2018a で導入参考
関数
pcregistercorr|pcregisterndt|pcregistercpd|pctransform|pcshowpair|pcshow|pcdownsample|pcfitplane|pcmerge|pcdenoise
