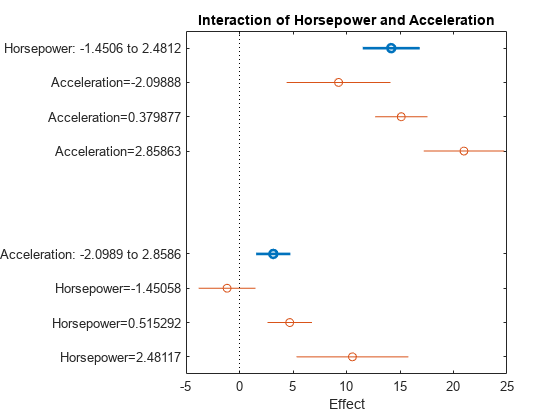
plotInteraction

線形回帰モデルの 2 つの予測子の交互作用効果のプロット

構文

plotInteraction(mdl,var1,var2)

plotInteraction(mdl,var1,var2,ptype)

plotInteraction(ax,___)

h = plotInteraction(___)

説明

plotInteraction(mdl,var1,var2) は、線形回帰モデル mdl で選択した 2 つの予測子 var1 および var2 の主効果およびその条件付き効果のプロットを作成します。効果の値を通る水平ラインは、95% 信頼区間を示します。

plotInteraction(mdl,var1,var2,ptype) は、プロット タイプ ptype を指定します。たとえば、ptype が 'predictions' である場合、plotInteraction は、1 番目の予測子を特定の値に固定した状態で 2 番目の予測子の関数として、調整された応答関数をプロットします。詳細については、条件付き効果を参照してください。

plotInteraction(ax,___) は、前の構文におけるいずれかの入力引数の組み合わせを使用して、現在の座標軸 (gca) ではなく ax によって指定される座標軸にプロットします。あるいは、最後の入力引数として Parent=ax を指定できます。 (R2024a 以降)

h = plotInteraction(___) は、line オブジェクトのベクトル h を返します。プロットの作成後に特定のラインのプロパティを修正するには、h を使用します。プロパティの一覧については、Line のプロパティを参照してください。

例

主効果および条件付き効果の交互作用プロット

交互作用項があるモデルを当てはめ、主効果および条件付き効果を示す交互作用プロットを作成します。

carsmall データ セットのデータを使用して、交互作用項が含まれている応答値を作成します。まず、データ セットを読み込み、予測子データを正規化します。

load carsmall
Acceleration = normalize(Acceleration); 
Horsepower = normalize(Horsepower);
Displacement = normalize(Displacement);

交互作用項 Acceleration*Horsepower が含まれている応答変数を定義します。

y = Acceleration + 4*Horsepower + Acceleration.*Horsepower + Displacement;

応答値にノイズを追加します。

rng('default') % For reproducibility
y = y + normrnd(10,0.25*std(y,'omitnan'),size(y));

予測子データと応答値が格納されている table を作成します。

tbl = table(Acceleration,Horsepower,Displacement,y);

線形回帰モデルを当てはめます。

mdl = fitlm(tbl,'y ~ Acceleration + Horsepower + Acceleration*Horsepower + Displacement + Horsepower*Displacement')

mdl = 
Linear regression model:
    y ~ 1 + Acceleration*Horsepower + Horsepower*Displacement

Estimated Coefficients:
                                Estimate       SE         tStat        pValue  
                               __________    _______    _________    __________

    (Intercept)                    9.8652    0.16177       60.982     8.587e-77
    Acceleration                  0.63726     0.1626       3.9191    0.00016967
    Horsepower                     3.6168       0.34       10.638     9.273e-18
    Displacement                  0.95032    0.31828       2.9858     0.0036144
    Acceleration:Horsepower       0.60108     0.1851       3.2473     0.0016209
    Horsepower:Displacement    -0.0096069    0.20947    -0.045863       0.96352


Number of observations: 99, Error degrees of freedom: 93
Root Mean Squared Error: 1.07
R-squared: 0.93,  Adjusted R-Squared: 0.927
F-statistic vs. constant model: 249, p-value = 3.3e-52

交互作用項 Acceleration*Horsepower の pValue は非常に小さいので、交互作用項が統計的に有意であることがわかります。

Horsepower と Acceleration の主効果および条件付き効果を示す交互作用プロットを作成します。

plotInteraction(mdl,'Horsepower','Acceleration')

各予測子について、主効果の点と条件付き効果の点が垂直には並んでいません。したがって、各予測子の主効果および条件付き効果の点に対する信頼区間を通る垂直線を見つけることはできません。このプロットは、応答変数に対する交互作用効果が存在することを示します。

比較のため、Displacement と Horsepower の交互作用プロットを作成します。この交互作用項 (Displacement*Horsepower) は p 値が大きいので、統計的に有意ではないことがわかります。

plotInteraction(mdl,'Displacement','Horsepower')

各予測子について、主効果の点と条件付き効果の点が垂直に並んでいます。このプロットは、交互作用がないことを示します。

調整された応答曲線の交互作用プロット

交互作用項があるモデルを当てはめ、調整された応答曲線の交互作用プロットを作成します。

carsmall データ セットのデータを使用して、交互作用項が含まれている応答値を作成します。まず、データ セットを読み込み、予測子データを正規化します。

load carsmall
Acceleration = normalize(Acceleration); 
Horsepower = normalize(Horsepower);
Displacement = normalize(Displacement);

交互作用項 Acceleration*Horsepower が含まれている応答変数を定義します。

y = Acceleration + 4*Horsepower + Acceleration.*Horsepower + Displacement;

応答値にノイズを追加します。

rng('default') % For reproducibility
y = y + normrnd(10,0.25*std(y,'omitnan'),size(y));

予測子データと応答値が格納されている table を作成します。

tbl = table(Acceleration,Horsepower,Displacement,y);

線形回帰モデルを当てはめます。

mdl = fitlm(tbl,'y ~ Acceleration + Horsepower + Acceleration*Horsepower + Displacement + Horsepower*Displacement')

mdl = 
Linear regression model:
    y ~ 1 + Acceleration*Horsepower + Horsepower*Displacement

Estimated Coefficients:
                                Estimate       SE         tStat        pValue  
                               __________    _______    _________    __________

    (Intercept)                    9.8652    0.16177       60.982     8.587e-77
    Acceleration                  0.63726     0.1626       3.9191    0.00016967
    Horsepower                     3.6168       0.34       10.638     9.273e-18
    Displacement                  0.95032    0.31828       2.9858     0.0036144
    Acceleration:Horsepower       0.60108     0.1851       3.2473     0.0016209
    Horsepower:Displacement    -0.0096069    0.20947    -0.045863       0.96352


Number of observations: 99, Error degrees of freedom: 93
Root Mean Squared Error: 1.07
R-squared: 0.93,  Adjusted R-Squared: 0.927
F-statistic vs. constant model: 249, p-value = 3.3e-52

交互作用項 Acceleration*Horsepower の pValue は非常に小さいので、交互作用項が統計的に有意であることがわかります。

Horsepower を特定の値に固定した Acceleration の関数として、調整された応答関数を示す、交互作用プロットを作成します。

plotInteraction(mdl,'Horsepower','Acceleration','predictions')

曲線は平行ではありません。このプロットは、予測子の間に交互作用があることを示します。

比較のため、Displacement と Horsepower の交互作用プロットを作成します。交互作用項 (Displacement*Horsepower) の p 値が大きいので、この交互作用項が統計的に有意ではないことがわかります。

plotInteraction(mdl,'Displacement','Horsepower','predictions')

曲線は平行なので、交互作用がないことがわかります。

入力引数

mdl — 線形回帰モデル オブジェクト

LinearModel オブジェクト | CompactLinearModel オブジェクト

線形回帰モデル オブジェクト。fitlm または stepwiselm を使用して作成した LinearModel オブジェクト、または compact を使用して作成した CompactLinearModel オブジェクトとして指定します。

var1 — プロットする 1 番目の変数

文字ベクトル | string 配列 | 正の整数

プロットする 1 番目の変数。mdl.VariableNames 内の変数名 (mdl の VariableNames プロパティ) を表す文字ベクトルまたは string 配列、または mdl.VariableNames 内の変数のインデックスを表す正の整数を指定します。

データ型: char | string | single | double

var2 — プロットする 2 番目の変数

文字ベクトル | string 配列 | 正の整数

プロットする 2 番目の変数。mdl.VariableNames 内の変数名 (mdl の VariableNames プロパティ) を表す文字ベクトルまたは string 配列、または mdl.VariableNames 内の変数のインデックスを表す正の整数を指定します。

データ型: char | string | single | double

ptype — プロット タイプ

'effects' (既定値) | 'predictions'

プロットのタイプ。次のいずれかの値を指定します。

• 'effects' — plotInteraction は、選択された 2 つの予測子 var1 および var2 の主効果およびその条件付き効果のプロットを作成します。効果の値を通る水平ラインは、95% 信頼区間を示します。

• 'predictions' — plotInteraction は、var1 を特定の値に固定した var2 の関数として、調整された応答関数をプロットします。

詳細は、主効果 と 条件付き効果 を参照してください。

ax — ターゲットの座標軸

Axes オブジェクト

R2024a 以降

ターゲットの座標軸。Axes オブジェクトを指定します。座標軸を指定しない場合、plotInteraction は現在の座標軸 (gca) を使用します。

出力引数

h — line オブジェクト

ベクトル

line オブジェクト。ベクトルとして返されます。line オブジェクトのプロパティのクエリと設定を行うには、ドット表記を使用します。詳細については、Line のプロパティ を参照してください。

プロット タイプが 'effects' (既定) である場合、h(1) は主効果の推定値を表す円に、h(2) と h(3) は 2 つの主効果の 95% 信頼区間に対応します。h の残りのエントリは、条件付き効果およびその信頼区間に対応します。主効果に関連付けられた line オブジェクトには、'main' というタグが付けられます。var1 および var2 の条件付き効果に関連付けられた line オブジェクトにはそれぞれ、'conditional1' および 'conditional2' というタグが付けられます。

プロット タイプが 'predictions' である場合、h の各エントリはプロットの各曲線に対応します。

詳細

主効果

予測子の効果 (主効果) は、他の予測子の効果を平均化して、ある予測子の値を変更した場合に、その予測子が応答に与える効果を表します。

予測子変数 x_s の効果は次のように定義されます。

g(x_si) – g(x_sj) ,

ここで、g は調整された応答関数です。関数 plotEffects は、観測値 i および j を以下のように選択します。順序変数ではないカテゴリカル変数の場合、x_si と x_sj はそれぞれ、調整された応答が最大および最小になる予測子の値です。したがって、効果の値は常に正です。数値変数または順序カテゴリカル変数の場合、調整された応答が最大および最小になる 2 つの予測子の値が選択されます。ここで、x_si < x_sj です。

plotEffects は、各予測子変数に対して、効果の値およびその 95% 信頼区間をプロットします。

調整された応答

調整された応答関数は、当てはめで使用したデータに対して当てはめた値の平均を求めることにより他の予測子を平均化して、当てはめた応答と単一の予測子の間の関係を表します。

予測子変数 (x₁, x₂, …, x_p) と応答変数 y に対する回帰モデルは、次のような形式になります。

y_i = f(x_1i, x_2i, …, x_pi) + r_i,

ここで、f は当てはめた回帰関数、r は残差です。添字 i は、観測値の番号に対応します。

たとえば、1 番目の予測子変数 x₁ に対する調整された応答関数は、次のように定義されます。

$$g\left(x_1\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}f\left(x_1,x_{2i},x_{3i},\mathrm{...},x_{pi}\right)},$$

ここで、n は観測値の個数です。調整された応答データ値は、調整された当てはめ値と残差を各観測値について合計した値です。

$${\tilde{y}}_i=g\left(x_{1i}\right)+r_i.$$

plotAdjustedResponse は、選択された予測子変数に対して、調整された応答関数と調整された応答データ値をプロットします。

条件付き効果

モデルに交互作用項が含まれている場合、ある予測子の主効果は、その予測子に作用する他の予測子の値によって変化します。このような場合、他の予測子の特定の値に対する、ある予測子の条件付き効果は、両方の予測子の実際の効果を理解するために役立ちます。条件付き効果の値を使用すると、ある予測子の効果が他の予測子の値に依存するかどうかを確認できます。

条件付き効果を定義するには、2 つの予測子変数の関数として、調整された応答関数を定義します。たとえば、x₁ と x₂ の調整された応答関数は、次のようになります。

$$h\left(x_1,x_2\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}f\left(x_1,x_2,x_{3i},\mathrm{...},x_{pi}\right)},$$

ここで、f は当てはめた回帰関数、n は観測値の個数です。

他の予測子の特定の値 (x_1k) に対する、ある予測子 (x₂) の条件付き効果は、次のように定義されます。

h(x_1k,x_2i) - h(x_1k,x_2j).

条件付き効果の値を計算するため、plotInteraction は、主効果を計算して x_1k の値を選択するときと同じ方法で、x₂ の観測値 i および j を選択します。x₁ がカテゴリカル変数である場合、plotInteraction は x₁ のすべての水準について条件付き効果を計算します。x₁ が数値変数である場合、plotInteraction は、x₁ の最小値、x₁ の最大値、および最小値と最大値の平均値という 3 つの x₁ の値について条件付き効果を計算します。

プロット タイプが 'effects' (既定) である場合、plotInteraction は、選択された 2 つの予測子の主効果、その条件付き効果、およびこれらの効果の値の 95% 信頼限界をプロットします。

プロット タイプが 'predictions' である場合、plotInteraction は、1 番目の予測子を特定の値に固定した状態で 2 番目の予測子の関数として、調整された応答関数をプロットします。たとえば、plotInteraction(mdl,'x1','x2','predictions') は、x_1k の各値について h(x_1k, x₂) の曲線をプロットします。

ヒント

• データ カーソルを使用すると、選択したプロットの点の値がデータ ヒント (データ点の横にある小さいテキスト ボックス) に表示されます。データ ヒントには、選択した点の x 軸および y 軸の値と、観測値の名前または番号が含まれます。

代替機能

• LinearModel オブジェクトには、複数のプロット関数が用意されています。

  • モデルを作成するときに、予測子変数の追加または削除による効果を理解するには、plotAdded を使用します。

  • モデルを検証するときに、問題があるデータを探し、各観測値の効果を理解するには、plotDiagnostics を使用します。また、モデルの残差を分析するには、plotResiduals を使用します。

  • モデルを当てはめた後で、特定の予測子の効果を理解するには、plotAdjustedResponse、plotPartialDependence および plotEffects を使用します。2 つの予測子の間の交互作用効果を理解するには、plotInteraction を使用します。また、予測曲面を通るスライスをプロットするには、plotSlice を使用します。

拡張機能

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2012a で導入

R2024a: ターゲットの座標軸の指定

プロットのターゲットの座標軸は、入力引数 ax または名前と値の引数 Parent=ax を使用して指定します。

参考

CompactLinearModel | LinearModel | plotAdjustedResponse | plotEffects

トピック

• 交互作用の影響による線形回帰
• 線形回帰の結果の解釈
• 線形回帰ワークフロー
• 線形回帰