交互作用の影響による線形回帰

交互作用効果がある線形回帰モデルを作成および分析し、結果を解釈します。

標本データを読み込みます。

load hospital

血圧の最初の列だけを保持するために、データを table に格納します。

tbl = table(hospital.Sex,hospital.Age,hospital.Weight,hospital.Smoker,hospital.BloodPressure(:,1), ...
    'VariableNames',{'Sex','Age','Weight','Smoker','BloodPressure'});

ステップワイズ線形回帰を実行します。

初期モデルとして、すべての項とそのペア単位の交互作用がある完全なモデルを使用します。

mdl = stepwiselm(tbl,'interactions')

1. Removing Sex:Smoker, FStat = 0.050738, pValue = 0.8223
2. Removing Weight:Smoker, FStat = 0.07758, pValue = 0.78124
3. Removing Age:Weight, FStat = 1.9717, pValue = 0.16367
4. Removing Sex:Age, FStat = 0.32389, pValue = 0.57067
5. Removing Age:Smoker, FStat = 2.4939, pValue = 0.11768

mdl = 
Linear regression model:
    BloodPressure ~ 1 + Age + Smoker + Sex*Weight

Estimated Coefficients:
                       Estimate       SE        tStat       pValue  
                       ________    ________    _______    __________

    (Intercept)         133.17       10.337     12.883      1.76e-22
    Sex_Male           -35.269       17.524    -2.0126      0.047015
    Age                0.11584     0.067664      1.712      0.090198
    Weight             -0.1393     0.080211    -1.7367      0.085722
    Smoker_1            9.8307       1.0229     9.6102    1.2391e-15
    Sex_Male:Weight     0.2341      0.11192     2.0917      0.039162


Number of observations: 100, Error degrees of freedom: 94
Root Mean Squared Error: 4.72
R-squared: 0.53,  Adjusted R-Squared: 0.505
F-statistic vs. constant model: 21.2, p-value = 4e-14

最終モデルの式の形式は BloodPressure ~ 1 + Age + Smoker + Sex*Weight となります。このモデルには 4 つの主効果 (年齢、喫煙、性別、体重) のすべてと、Sex と Weight の間にある 2 次交互作用が含まれています。このモデルは以下に対応します。

$B P = β_{0} + β_{A} X_{A} + β_{S m} I_{S m} + β_{S} I_{S} + β_{W} X_{W} + β_{S W} X_{W} I_{S} + ϵ,$

ここで

$B P$ は血圧
$β_{i}$ は係数
$I_{S m}$ は喫煙に関する指標変数。 $I_{S m} = 1$ は喫煙患者を表し、 $I_{S m} = 0$ は非喫煙患者を表す
$I_{S}$ は性別に関する指標変数。 $I_{S} = 1$ は男性患者を表し、 $I_{S} = 0$ は女性患者を表す
$X_{A}$ は変数 Age
$X_{W}$ は変数 Weight
$ϵ$ は誤差項

次の表では、それぞれの性別と喫煙の有無との組み合わせに当てはめられた近似線形モデルを説明します。

$\begin{array}{ccc} I_{S m} & I_{S} & Linear Model \\ 1 (Smoker) & 1 (Male) & \begin{aligned} B P & = (β_{0} + β_{S m} + β_{S}) + β_{A} X_{A} + (β_{W} + β_{S W}) X_{W} \\ {B P}_{}^{ˆ} & = 107.5617 + 0.11584 X_{A} + 0.11826 X_{W} \end{aligned} \\ 1 (Smoker) & 0 (Female) & \begin{aligned} B P & = (β_{0} + β_{S m}) + β_{A} X_{A} + β_{W} X_{W} \\ {B P}_{}^{ˆ} & = 143.0007 + 0.11584 X_{A} - 0.1393 X_{W} \end{aligned} \\ 0 (Nonsmoker) & 1 (Male) & \begin{aligned} B P & = (β_{0} + β_{S}) + β_{A} X_{A} + (β_{W} + β_{S W}) X_{W} \\ {B P}_{}^{ˆ} & = 97.901 + 0.11584 X_{A} + 0.11826 X_{W} \end{aligned} \\ 0 (Nonsmoker) & 0 (Female) & \begin{aligned} B P & = β_{0} + β_{A} X_{A} + β_{W} X_{W} \\ {B P}_{}^{ˆ} & = 133.17 + 0.11584 X_{A} - 0.1393 X_{W} \end{aligned} \end{array}$

これらのモデルからわかるように、 $β_{S m}$ と $β_{S}$ は、指標変数の値が 0 の場合と 1 の場合を比較して応答関数の切片がどの程度変化するかを表しています。一方、 $β_{S W}$ は、性別の指標変数の値が 0 の場合と 1 の場合を比較して、変数 Weight が応答変数にどのような影響を与えているかを表しています。最終モデルの主効果と交互作用効果は、次のように LinearModel クラスのメソッドで調べることができます。

予測スライスプロットをプロットします。

figure
plotSlice(mdl)

{"String":"Figure Prediction Slice Plots contains 4 axes objects and other objects of type uimenu, uicontrol. Axes object 1 contains 5 objects of type line. Axes object 2 contains 5 objects of type line. Axes object 3 contains 5 objects of type line. Axes object 4 contains 5 objects of type line.","Tex":[],"LaTex":[]}

このプロットは、すべての予測子変数の主効果を表しています。各パネルの緑色の線は、応答変数の変化を予測子変数の関数として表したものです (他の予測子変数がすべて一定であることが前提です)。たとえば、喫煙する 37.5 歳の男性患者の場合、他の条件が同じであれば、体重が大きくなると想定血圧も高くなります。

各パネルにある赤色の破線の曲線は、予測された応答値の 95% 信頼限界を表しています。

各パネルにある破線の横線は、破線の縦線に対応する予測子変数の特定の値に対して予測された応答を表しています。これらの線をドラッグすると、次のように、他の予測値について予測された応答値を表示できます。

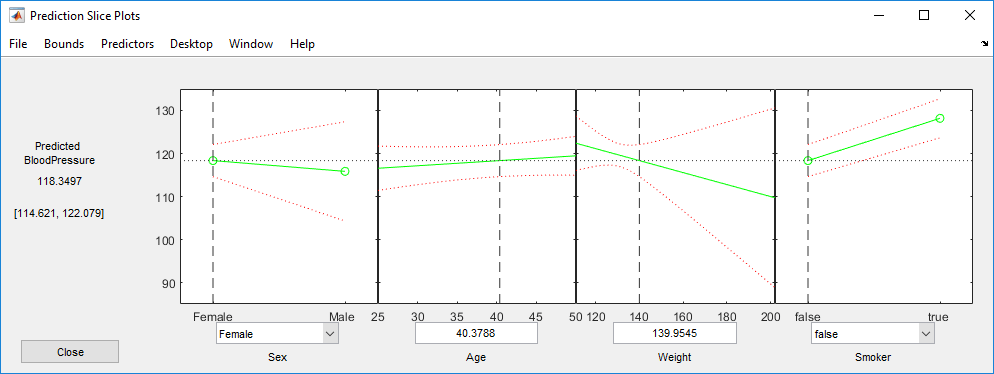
たとえば、喫煙しない女性患者で、年齢が 40.3788 歳、体重が 139.9545 ポンドの場合、応答変数の予測値は 118.3497 です。大かっこ内にある値 [114.621, 122.079] は、推定応答の 95% 信頼区間の下限と上限を表しています。喫煙しない女性患者については、他の条件が一定であれば、体重が大きいほど想定血圧は低くなります。

主効果をプロットします。

plotEffects(mdl)

Figure contains an axes object. The axes object contains 6 objects of type line.

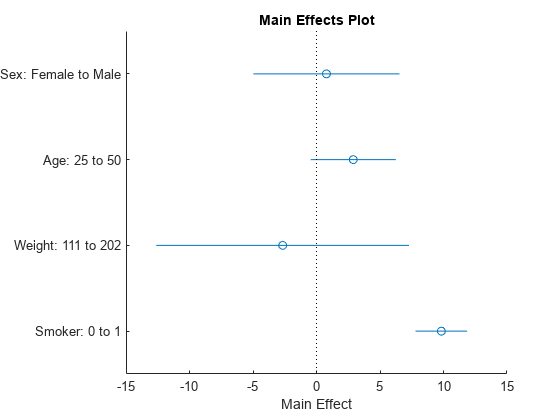
このプロットには主効果が表示されます。円は効果の大きさを表し、青色の線は主効果の信頼区間の上限と下限を表します。たとえば、他の条件が一定であれば、喫煙者の想定血圧は非喫煙者より 10 単位高くなります。また、他の条件が一定であれば、女性より男性のほうが想定血圧は 2 単位高くなります。さらに、他の条件が一定であれば、25 歳の人が 50 歳になると想定血圧が 4 単位高くなり、体重が 111 ポンドの人が 202 ポンドまで増えると 4 単位低くなると予想されます。

交互作用効果をプロットします。

figure
plotInteraction(mdl,'Sex','Weight')

Figure contains an axes object. The axes object with title Interaction of Sex and Weight contains 11 objects of type line.

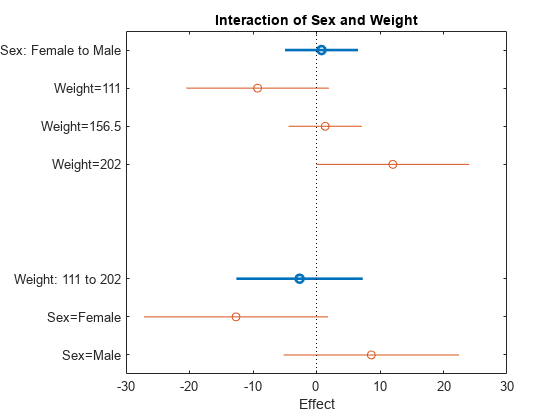
このプロットには、他の要因が一定の値で固定されている状態で、1 つの要因が変化した場合の影響が表示されます。

交互作用効果の解釈には注意が必要です。すべての要因の組み合わせに関するデータが十分でない場合、またはデータの相関関係が非常に強い場合は、他の要因が固定されている状態で、1 つの要因の変化の交互作用効果を判定するのは難しい場合があります。このような場合、推定された交互作用効果はデータからの外挿です。

青い円は、主効果のプロットの場合と同様に、特定の項の主効果を表します。赤い円は、他の項の値が固定されている状態で 1 つの項が変化した場合の影響を表します。たとえば、このプロットの下半分の赤い円は、女性患者と男性患者の体重の変化による影響を個別に表しています。女性患者の体重が 111 ポンドから 202 ポンドに増加すると想定血圧は 14 単位低くなりますが、男性患者の体重が同じだけ増加すると想定血圧は 5 単位高くなります (これも、他の予測子が同じであることが前提です)。

予測効果をプロットします。

figure
plotInteraction(mdl,'Sex','Weight','predictions')

Figure contains an axes object. The axes object with title Interaction of Sex and Weight contains 3 objects of type line. These objects represent Sex, Female, Male.

このプロットには、他の変数が一定である状態で 1 つの変数が変化した場合の効果が表示されます。この例では、最後の図は応答変数 (血圧) が体重の関数として表示されます。ここでは変数 sex は男性と女性で固定されています。男性と女性の線は交差しています。これは、体重と性別の間に強い交互作用があることを示しています。男性患者については体重が増加すると想定血圧が上昇し、女性患者については体重が増加すると想定血圧が低下していることがわかります。

参考