ステップワイズ回帰

ステップワイズ回帰による適切なモデルの選択

stepwiselm は線形モデルを作成し、モデルに対して自動的に追加またはトリムを行います。小さなモデルを作成するには、定数モデルから開始します。大きなモデルを作成するには、多数の項を含むモデルから開始します。通常、大きなモデルのほうが元のデータへの近似で測定される誤差は少なくなりますが、新しいデータを予測する際にはメリットがない可能性があります。

stepwiselm は fitlm のすべての名前と値のペアと、モデルの開始と範囲決めに関する追加オプションを使用できます。次に例を示します。

小さなモデルの場合、既定の下限モデルから開始します。'constant' (予測子の項をもたないモデル)
既定の上限モデルは線形項と交互作用項 (予測子のペアの乗算) をもちます。同じく二乗項を含む上限モデルの場合、Upper 名前と値のペアを 'quadratic' に設定します。

大小のステップワイズモデルの比較

ライブスクリプトを開く

この例では、定数モデルから開始した場合と完全交互作用モデルから開始した場合に stepwiselm から返されるモデルを比較する方法を示します。

carbig データを読み込み、このデータの一部をもとにテーブルを作成します。

load carbig
tbl = table(Acceleration,Displacement,Horsepower,Weight,MPG);

定数モデルから開始する燃料モデルのステップワイズを作成します。

mdl1 = stepwiselm(tbl,'constant','ResponseVar','MPG')

1. Adding Weight, FStat = 888.8507, pValue = 2.9728e-103
2. Adding Horsepower, FStat = 3.8217, pValue = 0.00049608
3. Adding Horsepower:Weight, FStat = 64.8709, pValue = 9.93362e-15

mdl1 = 
Linear regression model:
    MPG ~ 1 + Horsepower*Weight

Estimated Coefficients:
                          Estimate         SE         tStat       pValue  
                         __________    __________    _______    __________

    (Intercept)              63.558        2.3429     27.127    1.2343e-91
    Horsepower             -0.25084      0.027279    -9.1952    2.3226e-18
    Weight                -0.010772    0.00077381    -13.921    5.1372e-36
    Horsepower:Weight    5.3554e-05    6.6491e-06     8.0542    9.9336e-15


Number of observations: 392, Error degrees of freedom: 388
Root Mean Squared Error: 3.93
R-squared: 0.748,  Adjusted R-Squared: 0.746
F-statistic vs. constant model: 385, p-value = 7.26e-116

完全交互作用モデルから開始する燃料モデルのステップワイズを作成します。

mdl2 = stepwiselm(tbl,'interactions','ResponseVar','MPG')

1. Removing Acceleration:Displacement, FStat = 0.024186, pValue = 0.8765
2. Removing Displacement:Weight, FStat = 0.33103, pValue = 0.56539
3. Removing Acceleration:Horsepower, FStat = 1.7334, pValue = 0.18876
4. Removing Acceleration:Weight, FStat = 0.93269, pValue = 0.33477
5. Removing Horsepower:Weight, FStat = 0.64486, pValue = 0.42245

mdl2 = 
Linear regression model:
    MPG ~ 1 + Acceleration + Weight + Displacement*Horsepower

Estimated Coefficients:
                                Estimate         SE         tStat       pValue  
                               __________    __________    _______    __________

    (Intercept)                    61.285        2.8052     21.847    1.8593e-69
    Acceleration                 -0.34401       0.11862       -2.9     0.0039445
    Displacement                -0.081198      0.010071    -8.0623    9.5014e-15
    Horsepower                   -0.24313      0.026068    -9.3265    8.6556e-19
    Weight                     -0.0014367    0.00084041    -1.7095      0.088166
    Displacement:Horsepower    0.00054236    5.7987e-05     9.3531    7.0527e-19


Number of observations: 392, Error degrees of freedom: 386
Root Mean Squared Error: 3.84
R-squared: 0.761,  Adjusted R-Squared: 0.758
F-statistic vs. constant model: 246, p-value = 1.32e-117

次の点に注意してください。

mdl1 には 4 つの係数 (Estimate 列) が含まれ、mdl2 には 6 つの係数が含まれます。
mdl1 の自由度調整済み決定係数は 0.746 です。これは mdl2 の自由度調整済み決定係数の 0.758 よりわずかに小さい (悪い) 値です。

完全 2 次モデルを上限とし、完全 2 次モデルからステップワイズを開始した燃料モデルを作成します。

mdl3 = stepwiselm(tbl,'quadratic','ResponseVar','MPG','Upper','quadratic');

1. Removing Acceleration:Horsepower, FStat = 0.075209, pValue = 0.78405
2. Removing Acceleration:Weight, FStat = 0.072756, pValue = 0.78751
3. Removing Horsepower:Weight, FStat = 0.12569, pValue = 0.72314
4. Removing Weight^2, FStat = 1.194, pValue = 0.27521
5. Removing Displacement:Weight, FStat = 1.2839, pValue = 0.25789
6. Removing Displacement^2, FStat = 2.069, pValue = 0.15114
7. Removing Horsepower^2, FStat = 0.74063, pValue = 0.39

これらの式を調べて、3 つのモデルの複雑度を比較します。

mdl1.Formula

ans = 
MPG ~ 1 + Horsepower*Weight

mdl2.Formula

ans = 
MPG ~ 1 + Acceleration + Weight + Displacement*Horsepower

mdl3.Formula

ans = 
MPG ~ 1 + Weight + Acceleration*Displacement + Displacement*Horsepower + Acceleration^2

モデルがより複雑になると、自由度調整済み $R^{2}$ の値はわずかに改善されます。

RSquared = [mdl1.Rsquared.Adjusted, ...
    mdl2.Rsquared.Adjusted, mdl3.Rsquared.Adjusted]

RSquared = 1×3

    0.7465    0.7580    0.7599

3 つのモデルの残差プロットを比較します。

subplot(3,1,1)
plotResiduals(mdl1)
subplot(3,1,2)
plotResiduals(mdl2)
subplot(3,1,3)
plotResiduals(mdl3)

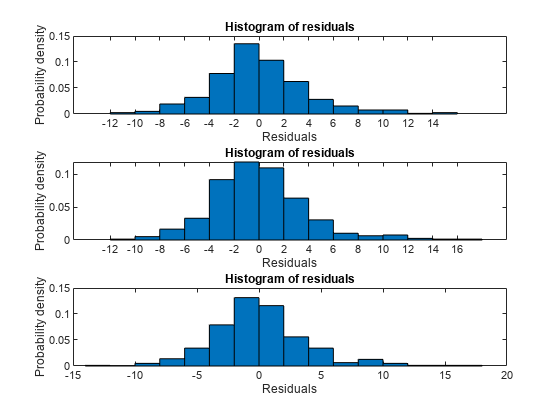
これらのモデルには同様の残差があります。どのモデルが最も適切にデータにあてはまるかは明確にはわかりません。

興味深いことに、より複雑なモデルほど残差の最大偏差が大きくなります。

Rrange1 = [min(mdl1.Residuals.Raw),max(mdl1.Residuals.Raw)];
Rrange2 = [min(mdl2.Residuals.Raw),max(mdl2.Residuals.Raw)];
Rrange3 = [min(mdl3.Residuals.Raw),max(mdl3.Residuals.Raw)];
Rranges = [Rrange1;Rrange2;Rrange3]

Rranges = 3×2

  -10.7725   14.7314
  -11.4407   16.7562
  -12.2723   16.7927

参考

fitlm | plotResiduals | stepwiselm | LinearModel