線形回帰ワークフロー

この例では、線形回帰モデルの当てはめ方法を示します。典型的なワークフローは、データのインポート、回帰の近似、品質テスト、品質改善のための変更、そして共有という流れです。

手順 1. データをテーブルにインポートする。

hospital.xls は、実験計画における患者の名前、性別、年齢、体重、血圧および治療日のデータが含まれている Excel® スプレッドシートです。最初にデータをテーブルに読み取ります。

patients = readtable('hospital.xls','ReadRowNames',true);

データの 5 行を調べます。

patients(1:5,:)

ans=5×11 table
                   name         sex     age    wgt    smoke    sys    dia    trial1    trial2    trial3    trial4
               ____________    _____    ___    ___    _____    ___    ___    ______    ______    ______    ______

    YPL-320    {'SMITH'   }    {'m'}    38     176      1      124    93       18       -99       -99       -99  
    GLI-532    {'JOHNSON' }    {'m'}    43     163      0      109    77       11        13        22       -99  
    PNI-258    {'WILLIAMS'}    {'f'}    38     131      0      125    83      -99       -99       -99       -99  
    MIJ-579    {'JONES'   }    {'f'}    40     133      0      117    75        6        12       -99       -99  
    XLK-030    {'BROWN'   }    {'f'}    49     119      0      122    80       14        23       -99       -99  

[sex] と [smoke] フィールドにはそれぞれ 2 つの選択肢があるようです。そのため、これらのフィールドを categorical に変更します。

patients.smoke = categorical(patients.smoke,0:1,{'No','Yes'});
patients.sex = categorical(patients.sex);

手順 2. 近似モデルを作成する。

この作業の目的は、患者の年齢、体重、性別および喫煙状況の関数として最大血圧をモデル化することです。'age'、'wgt'、'sex' および 'smoke' の関数として 'sys' の線形式を作成します。

modelspec = 'sys ~ age + wgt + sex + smoke';
mdl = fitlm(patients,modelspec)

mdl = 
Linear regression model:
    sys ~ 1 + sex + age + wgt + smoke

Estimated Coefficients:
                   Estimate        SE        tStat        pValue  
                   _________    ________    ________    __________

    (Intercept)       118.28      7.6291      15.504    9.1557e-28
    sex_m            0.88162      2.9473     0.29913       0.76549
    age              0.08602     0.06731       1.278       0.20438
    wgt            -0.016685    0.055714    -0.29947       0.76524
    smoke_Yes          9.884      1.0406       9.498    1.9546e-15


Number of observations: 100, Error degrees of freedom: 95
Root Mean Squared Error: 4.81
R-squared: 0.508,  Adjusted R-Squared: 0.487
F-statistic vs. constant model: 24.5, p-value = 5.99e-14

性別、年齢および体重の予測子は $$p$$ 値がかなり大きいので、これらの予測子の一部は不要である可能性があります。

手順 3. 外れ値を特定して削除する。

近似から除外する外れ値がデータ内に存在するかどうかを確認します。残差をプロットします。

plotResiduals(mdl)

外れ値の可能性があるデータが 1 つあります。値が 12 より大きいデータです。これは実際には外れ値でないかもしれません。外れ値を特定して削除する方法を、次に説明します。

外れ値を検出する。

outlier = mdl.Residuals.Raw > 12;
find(outlier)

ans = 84

外れ値を削除する。

mdl = fitlm(patients,modelspec,...
    'Exclude',84);

mdl.ObservationInfo(84,:)

ans=1×4 table
               Weights    Excluded    Missing    Subset
               _______    ________    _______    ______

    WXM-486       1        true        false     false 

観測 84 はモデル内に存在しなくなります。

手順 4. モデルを単純化する。

同等の予測精度をもちながら、予測子がより少ない簡潔なモデルの取得を試みます。step で一度に 1 つの項を追加または削除し、より優れたモデルを探究します。step では最大 10 のステップを実行できます。

mdl1 = step(mdl,'NSteps',10)

1. Removing wgt, FStat = 4.6001e-05, pValue = 0.9946
2. Removing sex, FStat = 0.063241, pValue = 0.80199

mdl1 = 
Linear regression model:
    sys ~ 1 + age + smoke

Estimated Coefficients:
                   Estimate       SE       tStat       pValue  
                   ________    ________    ______    __________

    (Intercept)     115.11       2.5364    45.383    1.1407e-66
    age            0.10782     0.064844    1.6628       0.09962
    smoke_Yes       10.054      0.97696    10.291    3.5276e-17


Number of observations: 99, Error degrees of freedom: 96
Root Mean Squared Error: 4.61
R-squared: 0.536,  Adjusted R-Squared: 0.526
F-statistic vs. constant model: 55.4, p-value = 1.02e-16

step は 2 つのステップを実行しました。これは、1 つの項を加算または減算しても、さらなるモデルの改良は期待できないことを意味します。

学習データで簡素化したモデルの効果をプロットします。

plotResiduals(mdl1)

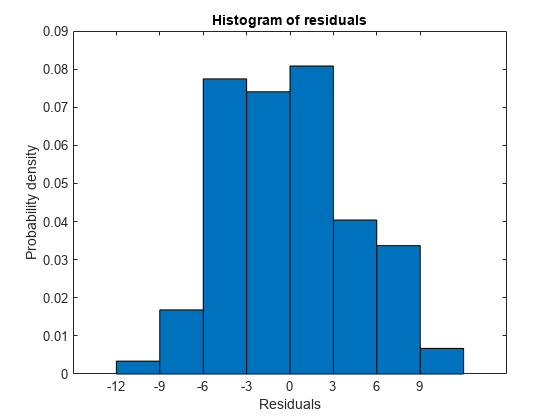
残差は元のモデルとほぼ同じくらい少ないことがわかります。

手順 5. 新しいデータへの応答を予測する。

新しい対象者が 4 人いるとします。各人の年齢は 25 歳、30 歳、40 歳、65 歳で、1 人目と 3 人目が喫煙者です。mdl1 を使用して最大血圧を予測します。

ages = [25;30;40;65];
smoker = {'Yes';'No';'Yes';'No'};
systolicnew = feval(mdl1,ages,smoker)

systolicnew = 4×1

  127.8561
  118.3412
  129.4734
  122.1149

予測するためには、mdl1 が使用する変数のみが必要です。

手順 6. モデルを共有する。

他のユーザーが予測のためにこのモデルを使用できるようにすることができます。線形モデルの項にアクセスします。

coefnames = mdl1.CoefficientNames

coefnames = 1x3 cell
    {'(Intercept)'}    {'age'}    {'smoke_Yes'}

モデル式を表示します。

mdl1.Formula

ans = 
sys ~ 1 + age + smoke

項の係数にアクセスします。

coefvals = mdl1.Coefficients(:,1).Estimate

coefvals = 3×1

  115.1066
    0.1078
   10.0540

モデルは sys = 115.1066 + 0.1078*age + 10.0540*smoke です。ここで smoke の値は、喫煙者が 1、非喫煙者が 0 です。

参考

fitlm | LinearModel | feval | step | plotResiduals

関連するトピック

• 線形回帰モデルとは
• 線形回帰
• 線形回帰の結果の解釈
• 交互作用の影響による線形回帰