plotAdded

線形回帰モデルの追加変数プロット

構文

plotAdded(mdl)

plotAdded(mdl,coef)

plotAdded(mdl,coef,Name,Value)

plotAdded(ax,___)

h = plotAdded(___)

説明

plotAdded(mdl) は、定数 (切片) 項を除くモデル mdl 全体に対する追加変数プロットを作成します。

plotAdded(mdl,coef) は、指定された項 coef に対する追加変数プロットを作成します。

plotAdded(mdl,coef,Name,Value) は、1 つ以上の名前と値のペアの引数を使用して、調整されたデータ点のグラフィック プロパティを指定します。たとえば、データ点のマーカー記号やサイズを指定できます。

plotAdded(ax,___) は、前の構文におけるいずれかの入力引数の組み合わせを使用して、現在の座標軸ではなく ax によって指定される座標軸にプロットを作成します。

h = plotAdded(___) は、プロット用の line オブジェクトを返します。プロットの作成後に特定のラインのプロパティを修正するには、h を使用します。プロパティの一覧については、Line のプロパティを参照してください。

例

追加変数プロットの作成

自動車の燃費の線形回帰モデルを重量とモデル年の関数として作成します。次に、追加変数プロットを作成して、モデルの有意性を確認します。

carsmall データ セットから燃費の線形回帰モデルを作成します。

load carsmall
Year = categorical(Model_Year);
tbl = table(MPG,Weight,Year);
mdl = fitlm(tbl,'MPG ~ Year + Weight^2');

モデルの追加変数プロットを作成します。

plot(mdl)

水平線が信頼限界の間に収まっていないので、このプロットはモデルが有意であることを示しています。

関数 plotAdded を使用して、同じプロットを作成します。

plotAdded(mdl)

指定した変数に対する追加変数プロットの作成

自動車の燃費の線形回帰モデルを重量とモデル年の関数として作成します。次に、追加変数プロットを作成して、重み付けの項 (Weight および Weight^2) の効果を確認します。

carsmall データ セットを使用して、線形回帰モデルを作成します。

load carsmall
Year = categorical(Model_Year);
tbl = table(MPG,Weight,Year);
mdl = fitlm(tbl,'MPG ~ Year + Weight^2');

Weight と Weight^2 に対応するモデル内の項を探します。

mdl.CoefficientNames

ans = 1×5 cell
    {'(Intercept)'}    {'Weight'}    {'Year_76'}    {'Year_82'}    {'Weight^2'}

重み付けの項は 2 と 5 です。

重み付けの項を使用して追加変数プロットを作成します。

coef = [2 5];
plotAdded(mdl,coef)

水平線が信頼限界の間に収まっていないので、このプロットは重みの項が有意であることを示しています。

単純な線形回帰の散布図の作成

単純な線形回帰モデルに対して、近似曲線と信頼限界が含まれているデータの散布図を作成します。単純な線形回帰モデルには、1 つの予測子変数のみを含めます。

carsmall データ セットから燃費の単純な線形回帰モデルを作成します。

load carsmall
tbl = table(MPG,Weight);
mdl = fitlm(tbl,'MPG ~ Weight')

mdl = 
Linear regression model:
    MPG ~ 1 + Weight

Estimated Coefficients:
                    Estimate        SE         tStat       pValue  
                   __________    _________    _______    __________

    (Intercept)        49.238       1.6411     30.002    2.7015e-49
    Weight         -0.0086119    0.0005348    -16.103    1.6434e-28


Number of observations: 94, Error degrees of freedom: 92
Root Mean Squared Error: 4.13
R-squared: 0.738,  Adjusted R-Squared: 0.735
F-statistic vs. constant model: 259, p-value = 1.64e-28

変数 Weight の pValue は非常に小さいので、この変数がモデル内で統計的に有意であることがわかります。関数 plot を使用して近似曲線と 95% 信頼限界が含まれているデータの散布図を作成することにより、この結果を可視化します。

plot(mdl)

水平線が信頼限界の間に収まらないので、このプロットはモデルが有意であることを示しています。これは pValue の結果と一致します。

関数 plotAdded を使用して、同じプロットを作成します。

plotAdded(mdl)

定数項と 1 つの項のみがモデルに含まれている場合、調整された値は元の値と同じです。したがって、この追加変数プロットは、関数 plot で作成した散布図と同じです。

入力引数

mdl — 線形回帰モデル

LinearModel オブジェクト

線形回帰モデル。fitlm または stepwiselm を使用して作成した LinearModel オブジェクトとして指定します。

coef — 回帰モデルの係数

文字ベクトル | string スカラー | 正の整数のベクトル

回帰モデル mdl の係数。次のいずれかを指定します。

• mdl.CoefficientNames (mdl の CoefficientNames プロパティ) 内の単一の係数名を表す文字ベクトルまたは string スカラー。

• mdl.CoefficientNames 内の係数のインデックスを表す正の整数のベクトル。ベクトルを使用して、複数の係数を指定します。

データ型: char | string | single | double

ax — ターゲットの座標軸

Axes オブジェクト

ターゲットの座標軸。Axes オブジェクトを指定します。

現在の座標軸が直交である場合に座標軸が指定されなかった場合、plotAdded は現在の座標軸 (gca) を使用します。Axes オブジェクトを作成する方法の詳細については、axes と gca を参照してください。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'Color','blue','Marker','*'

メモ

ここでは、グラフィック プロパティの一部だけを紹介しています。完全な一覧については、Line のプロパティ を参照してください。指定したプロパティによって、調整されたデータ点の外観が決まります。

Color — ラインの色

RGB 3 成分 | 16 進数のカラー コード | 色の名前 | 省略名

ラインの色。RGB 3 成分、16 進数カラー コード、あるいは以下の表に記載されているいずれかの色オプションに対応する色の名前または省略名として指定します。

MarkerEdgeColor が "auto" (既定) であり MarkerFaceColor が "auto" である場合、名前と値の引数 Color はマーカーの輪郭の色とマーカーの塗りつぶし色も決定します。

カスタム色の場合は、RGB 3 成分または 16 進数のカラー コードを指定します。

• RGB 3 成分は、色の赤、緑、青成分の強度を指定する 3 要素の行ベクトルです。強度は範囲 [0,1] に含まれていなければなりません。たとえば [0.4 0.6 0.7] のようになります。

• 16 進数のカラー コードは、ハッシュ記号 (#) で始まり、0 から F の範囲にある 16 進数が 3 つまたは 6 つ続く、string スカラーまたは文字ベクトルです。この値では、大文字と小文字は区別されません。したがって、カラー コード "#FF8800"、"#ff8800"、"#F80"、"#f80" は等価です。

あるいは、一部の一般的な色を名前で指定できます。次の表は、名前が付いた色のオプション、等価な RGB 3 成分、および 16 進数カラー コードの一覧です。

色の名前	省略名	RGB 3 成分	16 進数のカラー コード	外観
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"
"none"	該当なし	該当なし	該当なし	色なし

次の表に、ライト テーマとダーク テーマのプロット用の既定のカラー パレットを示します。

パレット	パレットの色
"gem" — ライト テーマの既定の設定 R2025a より前: ほとんどのプロットでは、これらの色が既定で使用されます。
"glow" — ダーク テーマの既定の設定

これらのパレットの RGB 3 成分と 16 進数カラー コードは、orderedcolors 関数と rgb2hex 関数を使用して取得できます。たとえば、"gem" パレットの RGB 3 成分を取得し、それらを 16 進数カラー コードに変換します。

RGB = orderedcolors("gem");
H = rgb2hex(RGB);

R2023b より前: RGB = get(groot,"FactoryAxesColorOrder") を使用して RGB 3 成分を取得します。

R2024a より前: H = compose("#%02X%02X%02X",round(RGB*255)) を使用して 16 進数カラー コードを取得します。

例: Color="blue"

データ型: single | double | string | char

LineWidth — ラインの幅

正の値

ラインの幅。ポイント単位の正の値として指定します。ラインにマーカーがある場合、ライン幅はマーカー エッジにも影響を与えます。

例: LineWidth=0.75

データ型: single | double

Marker — マーカー記号

"o" | "+" | "*" | "." | "x" | ...

マーカー記号。次の表のいずれかの値として指定します。

マーカー	説明	結果として得られるマーカー
"o"	円
"+"	プラス記号
"*"	アスタリスク
"."	点
"x"	十字
"_"	水平線
"|"	垂直線
"square"	正方形
"diamond"	菱形
"^"	上向き三角形
"v"	下向き三角形
">"	右向き三角形
"<"	左向き三角形
"pentagram"	星形五角形
"hexagram"	星形六角形
"none"	マーカーなし	該当なし

例: Marker="+"

データ型: string | char

MarkerEdgeColor — マーカーの輪郭の色

"auto" (既定値) | "none" | RGB 3 成分 | 16 進数のカラー コード | 色の名前 | 省略名

マーカーの輪郭の色。RGB 3 成分、16 進数カラー コード、あるいは名前と値の引数 Color に記載されているいずれかの色オプションに対応する色の名前または省略名として指定します。

既定値 "auto" では、名前と値の引数 Color を使用して指定されるものと同じ色が使用されます。色なしとして "none" を指定することもできます。

例: MarkerEdgeColor="blue"

データ型: single | double | string | char

MarkerFaceColor — マーカーの塗りつぶし色

"none" (既定値) | "auto" | RGB 3 成分 | 16 進数のカラー コード | 色の名前 | 省略名

マーカーの塗りつぶしの色。RGB 3 成分、16 進数カラー コード、あるいは名前と値の引数 Color に記載されているいずれかの色オプションに対応する色の名前または省略名として指定します。既定値の "none" は色なしを指定します。

値 "auto" では、名前と値の引数 Color を使用して指定されるものと同じ色が使用されます。

例: MarkerFaceColor="blue"

データ型: single | double | string | char

MarkerSize — マーカー サイズ

6 (既定値) | 正の値

マーカーのサイズ。ポイント単位の正の値として指定します。

例: MarkerSize=2

データ型: single | double

出力引数

h — line オブジェクト

ベクトル

line オブジェクト。3 行 1 列のベクトルとして返されます。h(1)、h(2)、h(3) はそれぞれ、調整されたデータ点、近似直線、近似直線の 95% 信頼限界に対応します。line オブジェクトのプロパティのクエリと設定を行うには、ドット表記を使用します。詳細については、Line のプロパティ を参照してください。

名前と値のペアの引数を使用して、1 番目のグラフィックス オブジェクト h(1) に対応する、調整されたデータ点の外観を指定できます。

詳細

追加変数プロット

追加変数プロット (偏回帰のてこ比のプロットとも呼ばれます) は、他のすべての項の効果を排除すると、指定した項が応答に与える効果がどの程度増加するかを示します。

単一の予測子変数に対応する単一の項を選択して plotAdded で作成した追加変数プロットには、以下のプロットが含まれます。

• 調整された予測子変数の値に対する調整された応答値の散布図

• 調整された予測子変数の値の関数としての、調整された応答値の近似直線

• 近似直線の 95% 信頼限界

調整された値は、選択した予測子を除くすべての予測子に当てはめた変数の残差を変数の平均値に加算した値です。たとえば、1 番目の予測子変数 x₁ に対する追加変数プロットを考えます。次のようにして、x₁ を除くすべての予測子に、応答変数 y および選択した予測子変数 x₁ を当てはめます。

y_i = g_y(x_2i, x_3i, …, x_pi) + r_yi,

x_1i = g_x(x_2i, x_3i, …, x_pi) + r_xi,

ここで、g_y と g_x はそれぞれ、選択した予測子 (x₁) を除くすべての予測子に対する y および x₁ の当てはめです。r_y と r_x は、対応する残差ベクトルです。添字 i は、観測値の番号に対応します。調整された値は、各観測値の残差と平均値の合計です。

$$\begin{array}{c}{\tilde{y}}_i=\overline{y}+r_{yi},\\ {\tilde{x}}_{1i}={\overline{x}}_1+r_{xi},\end{array}$$

ここで、$${\overline{x}}_1$$ と $$\overline{y}$$ はそれぞれ x₁ および y の平均を表します。

plotAdded は、($${\tilde{x}}_{1i}$$, $${\tilde{y}}_i$$) の散布図、$$\tilde{y}$$ の関数としての $${\tilde{x}}_1$$ の近似直線 (つまり $${\beta }_1{\tilde{x}}_1$$)、および近似直線の 95% 信頼限界をプロットします。係数 β₁ は、すべての予測子が含まれている完全なモデルにおける x₁ の係数推定値と同じです。

r_yi は、応答値の中で (x₁ を除く) 予測子では説明できない部分を表します。r_xi は、x₁ の値の中で他の予測子では説明できない部分を表します。したがって、近似直線は、x₁ を追加することによって導入される新しい情報が、応答値の説明できない部分をどのように説明できるかを表します。近似直線の傾きがゼロに近く、信頼限界に水平線を含めることができる場合、プロットは x₁ による新しい情報によっても応答値の説明できない部分を説明できないことを示します。つまり、x₁ はモデルの当てはめにおいて有意ではありません。

plotAdded は、単一の項ではなく複数の項を選択できる、追加変数プロットの拡張機能もサポートします。したがって、カテゴリカル予測子、特定の予測子に関係するすべての項、または (定数 (切片) 項を除く) モデル全体も指定できます。係数ベクトル β をもつ予測子の集合 X を考えます。ここで、i 番目の係数を追加変数プロットに対して指定した場合、β_i は完全なモデルにおける x_i の係数推定値です。それ以外の場合、β_i はゼロです。単位方向ベクトル u を u = β/s として定義します。ここで、s = norm(β) です。すると、Xβ = (Xu)s になります。係数 s をもつ単一の予測子として Xu を扱い、単一の項に対してプロットを作成する場合と同じ方法で Xu に対する追加変数プロットを作成します。この追加変数プロットにおける近似直線の係数は、s に対応します。

ヒント

• データ カーソルを使用すると、選択したプロットの点の値がデータ ヒント (データ点の横にある小さいテキスト ボックス) に表示されます。データ ヒントには、選択した点の x 軸および y 軸の値と、観測値の名前または番号が含まれます。

代替機能

• LinearModel オブジェクトには、複数のプロット関数が用意されています。

  • モデルを作成するときに、予測子変数の追加または削除による効果を理解するには、plotAdded を使用します。

  • モデルを検証するときに、問題があるデータを探し、各観測値の効果を理解するには、plotDiagnostics を使用します。また、モデルの残差を分析するには、plotResiduals を使用します。

  • モデルを当てはめた後で、特定の予測子の効果を理解するには、plotAdjustedResponse、plotPartialDependence および plotEffects を使用します。2 つの予測子の間の交互作用効果を理解するには、plotInteraction を使用します。また、予測曲面を通るスライスをプロットするには、plotSlice を使用します。

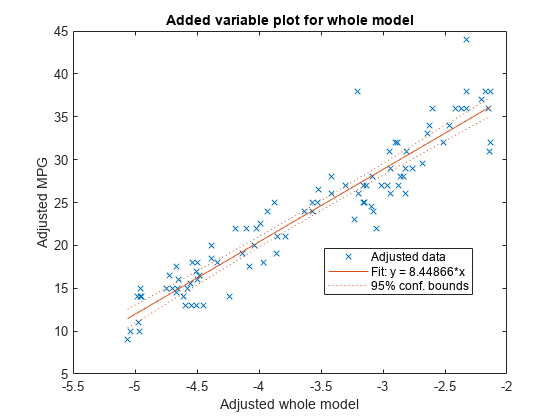
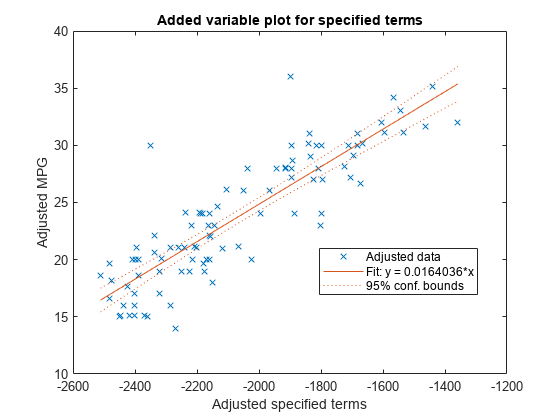
• plotAdded は、他の項の効果を排除すると、指定した項が応答に与える効果がどの程度増加するかを示します。これに対して plotAdjustedResponse は、当てはめた値の平均を求めることにより他の予測子を平均化して、モデルの当てはめにおける選択した予測子の効果を示します。plotAdded と plotAdjustedResponse では調整された値の定義が異なることに注意してください。

拡張機能

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2012a で導入

参考

LinearModel | plot

トピック

• 線形回帰ワークフロー
• 線形回帰の結果の解釈
• 線形回帰