AWGN Channel

ホワイト ガウス ノイズの入力信号への付加

• 

ライブラリ:
Communications Toolbox / Channels

説明

AWGN Channel ブロックは入力信号にホワイト ガウス ノイズを付加します。サンプル時間を入力信号から継承します。

例

符号化された信号の AWGN Channel ブロックの使用

シミュレーションで符号化を使用する場合、AWGN チャネル用の Eb/N0 設定は、必要な S/N 比 (SNR) を適用するために符号化率で調整しなければなりません。

slex_hamming_check.slx モデルは、AWGN チャネル経由でフィルター処理された BPSK 変調信号に対して前方誤り訂正 (FEC) 符号化を実行します。このモデルは、BPSK Modulator Baseband、AWGN Channel、およびBPSK Demodulator Basebandの離散ブロックを使用して、バイナリ対称チャネルをシミュレートします。符号化された Eb/N0 と符号化されていない Eb/N0 (Eb/N0) の差を考慮するために、AWGN Channel ブロックは符号化された Eb/N0 を Eb/N0 + 10log10(K/N) dB として計算します。ここで、K/N は符号化率、Eb/N0 は符号化されていない Eb/N0 です。Hamming Encoderブロックの入力ビット期間は 1 秒で、出力ビット期間は符号化率係数 K/N を掛けた 4/7 秒に減少します。符号化率により、"バイナリ対称チャネル" のビット期間は 4/7 秒になります。

モデルは、コールバック関数 PreLoadFcn を使用して、ブロック パラメーターの構成に使用する変数を初期化します。詳細については、モデル コールバック (Simulink)を参照してください。

model = 'slex_hamming_check';
open_system(model);

AWGN Channel ブロックは、変調信号に基づいて "シンボルあたりのビット数" および "Input signal power, referenced to 1 ohm (watts)" パラメーター設定も構成しなければなりません。この例では BPSK 変調を使用しているため、AWGN Channel ブロックのシンボルあたりのビット数は 1 に設定されています。モデルには、AWGN Channel ブロックの入力信号強度に必要な設定を確認するために、AWGN 入力での信号強度を測定するPower Meterブロックが含まれます。

エラー レートの結果とプロットを作成して、シミュレーションと理論を比較します。符号化された信号の理論的なチャネル誤り確率は Q(sqrt(2*Ebc/N0)) です。ここで、Q() は標準の Q 関数、Ebc/N0 は線形単位 (dB 単位ではない) の符号化された Eb/N0 です。関数 bercoding を使用し、Eb/N0 値の範囲にわたる AWGN 環境下での BPSK 変調信号に対して、線形の理論上の BER 上限、最小距離 3 での符号化率 4/7 のブロック符号、および硬判定復号化を計算します。同じ範囲の Eb/N0 値にわたって slex_hamming_check モデルをシミュレーションします。

EbNoVec = 0:2:10;
theorBER = bercoding(EbNoVec,'block','hard',7,4,3);

berVecBSC  = zeros(length(EbNoVec),3);
for n   = 1:length(EbNoVec)
    EbNo = EbNoVec(n);
    sim(model);
    berVecBSC(n,:) = berBSC(end,1);
end

関数semilogyを使用して結果をプロットすると、ほぼ同じ結果が表示されます。モデルには、200 個のエラーが発生する、またはブロックが 1x10^6 個のビットを受信するまで各 Eb/N0 点を実行するように構成されたError Rate Calculationブロックがあります。

semilogy( ...
    EbNoVec,berVecBSC(:,1),'d', ...
    EbNoVec,theorBER,'-');
legend('BSC BER','Theoretical BER', ...
    Location="southwest");
xlabel("Eb/N0 (dB)");
ylabel("Error Probability");
title("Bit Error Probability");
grid on;

Simulink での LLR と硬判定復調

このモデルでは、畳み込み符号化された通信リンクで、硬判定復調の代わりに対数尤度比 (LLR) を使用すると、BER 性能が向上することを示します。

この例の MATLAB® バージョンについては、対数尤度比 (LLR) 復調を参照してください。

システム設定

このモデル例では、1 つの送信側、1 つの AWGN チャネル、および 3 つの受信側をもつ、畳み込み符号化された通信システムをシミュレートします。畳み込み符号化器の符号化率は 1/2 です。システムでは 16-QAM 変調を採用しています。変調信号は加法性ホワイト ガウス ノイズ チャネルを通過します。一番上の受信側は、硬判定復調を行うように設定されているビタビ復号化器と組み合わせて、硬判定復調を行います。2 番目の受信側には、対数尤度比 (LLR) を計算するように構成されている復調器があり、3 ビットの量子化器を使用して量子化されます。最適な性能を得るには、量子化レベルがノイズ分散に依存していることはよく知られています [2]。量子化器の正確な境界は、ここで経験的に調べます。軟判定復号化を行うように設定されているビタビ復号化器は、これらの量子化された値を処理します。復調器によって計算された LLR 値に -1 を乗算し、ビタビ復号化器で使用する適切な量子化器インデックスに割り当てます。LLR を計算するには、入力時にわかっているノイズ分散を復調器に指定しなければなりません。3 番目の受信側には、非量子化モードで設定されているビタビ復号化器によって処理される LLR を計算する復調器が含まれています。各受信機の BER 性能が計算され、表示されます。

modelName = 'commLLRvsHD';
open_system(modelName);

システム シミュレーションと可視化

さまざまな情報ビットの Eb/No 値にわたって、このシステムをシミュレートします。コード ビットおよびマルチ ビットのシンボルについてこれらの Eb/No 値を調整して、AWGN ブロックおよび Rectangular QAM Baseband Demodulator ブロックに必要なノイズ分散値を取得します。Eb/No 値ごとの BER 結果を収集し、結果を可視化します。

EbNo     = 2:0.5:8; % information rate Eb/No in dB
codeRate = 1/2;     % code rate of convolutional encoder
nBits    = 4;       % number of bits in a 16-QAM symbol
Pavg     = 10;      % average signal power of a 16-QAM modulated signal
snr      = EbNo - 10*log10(1/codeRate) + 10*log10(nBits); % SNR in dB
noiseVarVector = Pavg ./ (10.^(snr./10)); % noise variance

% Initialize variables for storing the BER results
ber_HD  = zeros(1,length(EbNo));
ber_SD  = zeros(1,length(EbNo));
ber_LLR = zeros(1, length(EbNo));

% Loop over all noiseVarVector values
for idx=1:length(noiseVarVector)
    noiseVar = noiseVarVector(idx); %#ok<NASGU>
    sim(modelName);
    % Collect BER results
    ber_HD(idx)  = BER_HD(1);
    ber_SD(idx)  = BER_SD(1);
    ber_LLR(idx) = BER_LLR(1);
end

% Perform curve fitting and plot the results
fitBER_HD  = real(berfit(EbNo,ber_HD));
fitBER_SD  = real(berfit(EbNo,ber_SD));
fitBER_LLR = real(berfit(EbNo,ber_LLR));
semilogy(EbNo,ber_HD,'r*', ...
    EbNo,ber_SD,'g*', ...
    EbNo,ber_LLR,'b*', ...
    EbNo,fitBER_HD,'r', ...
    EbNo,fitBER_SD,'g', ...
    EbNo,fitBER_LLR,'b');
legend('Hard Decision Decoding', ...
    'Soft Decision Decoding','Unquantized Decoding');
xlabel('Eb/No (dB)');
ylabel('BER');
title('LLR vs. Hard Decision Demodulation with Viterbi Decoding');
grid on;

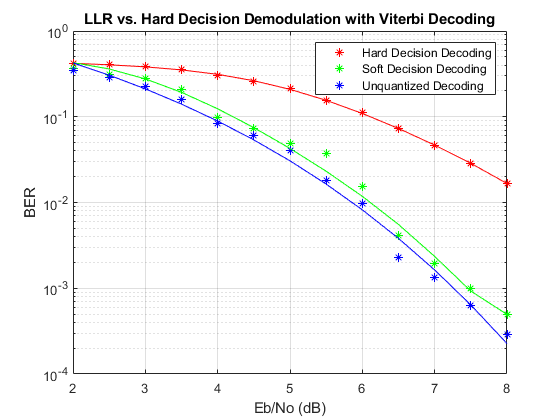
このシステムをさらに実験するには、別の変調タイプを試してください。このシステムでは、より高速で誤りを訂正するためバイナリ マッピング方式の変調スキームを使用しますが、グレイ マッピング方式の信号コンスタレーションの方が BER 性能が高いことがよく知られています。変調器および復調器のブロック内で、さまざまなコンスタレーション順序オプションで実験します。近似 LLR を計算するように復調器ブロックを構成して、硬判定復調および LLR と比較した BER 性能の違いを調べます。さまざまな Eb/No 値で実験してみます。さらに、変調スキームと Eb/No 値についてさまざまな量子化器の境界を調べます。

Simulink でのデータフローの使用

この例では、Dataflow Subsystem の [領域] パラメーターをデータフローに設定することで、データ駆動型の実行を使用するように構成できます。データフローを使用して、領域内のブロックは、Simulink® のサンプル タイミングではなく使用可能なデータに基づいて実行します。Simulink はシステムをコンカレント スレッドに自動的に分割します。この自動分割はシミュレーションを高速化し、データ スループットを増やします。データフローと、複数のスレッドを使用してこの例を実行する方法の詳細については、比較する復調タイプのマルチコア シミュレーションを参照してください。

% Cleanup
close_system(modelName,0);
clear modelName EbNo codeRate nBits Pavg snr noiseVarVector ...
    ber_HD ber_SD ber_LLR idx noiseVar fitBER_HD fitBER_SD fitBER_LLR;

参考文献

[1] J. L. Massey, "Coding and Modulation in Digital Communications", Proc.Int. Zurich Seminar on Digital Communications, 1974

[2] J. A. Heller, I. M. Jacobs, "Viterbi Decoding for Satellite and Space Communication", IEEE® Trans.Comm. Tech. vol COM-19, October 1971

Simulink を使用した AWGN チャネルのグレイ符号 M-PSK 変調エラー レート

この例では、doc_gray_code を使用して、M-PSK 変調のビット エラー レート (BER) とシンボル エラー レート (SER) を計算します。AWGN 環境下での M-PSK 変調の理論上のエラー レート性能を、グレイ符号シンボル マッピングのエラー レート性能およびバイナリ符号シンボル マッピングのエラー レート性能と比較します。

Random Integer Generator ブロックはソースとして機能し、整数のシーケンスを生成します。Integer to Bit Converter ブロックは、各整数を対応するバイナリ表現に変換します。doc_gray_code モデルのM-PSK Modulator Basebandブロックは、次を行います。

• [0, (M - 1] の範囲の整数を表すバイナリ値の入力を受け入れる。ここで、M は変調次数です。

• グレイ符号の順序付けを使用して、バイナリ表現をコンスタレーション点に割り当てる。

• [0, (2 (M - 1) / M)] の範囲の等間隔の位相をもつ、単位振幅の複素フェーザ出力を生成する。

AWGN Channel ブロックは、変調されたデータにホワイト ガウス ノイズを付加します。M-PSK Demodulator Baseband ブロックは、ノイズを含むデータを復調します。Bit to Integer Converter ブロックは、各バイナリ表現を、対応する整数に変換します。次に、2 つの個別のError Rate Calculationブロックが、復調されたデータのエラー レートを計算します。"SER Calculation" というラベルの付いたブロックは整数データを比較してシンボル エラー レートの統計を計算し、"BER Calculation" というラベルの付いたブロックはビット データを比較してビット エラー レートの統計を計算します。Error Rate Calculation ブロックの出力は、計算されたエラー レート、観察された誤り数、および処理されたデータ量を含む 3 要素ベクトルになります。

シミュレーションの実行時間を短縮し、かつ Eb/N0 比が増加してもエラーの統計値が確実に安定するように、モデルは 100 個のエラーが発生するか 1e8 ビットが送信されるまで実行するように構成されています。

モデルは、コールバック関数 PreLoadFcn を使用して、ブロック パラメーターの構成に使用する変数を初期化します。詳細については、モデル コールバック (Simulink)を参照してください。

エラー レート曲線の生成

関数berawgnを使用して、AWGN 環境下での非差分 8-PSK の理論上の BER を Eb/N0 値の範囲にわたって計算します。グレイ符号シンボル マッピングを使用し、同じ範囲の Eb/N0 値にわたって doc_gray_code モデルをシミュレーションします。

"Constellation orders" パラメーターを Gray ではなく Binary に設定するように M-PSK Modulator Baseband ブロックと M-PSK Demodulator Baseband ブロックを変更して、グレイ符号化とバイナリ符号化を比較します。バイナリ符号シンボル マッピングを使用し、同じ範囲の Eb/N0 値にわたって doc_gray_code モデルをシミュレーションします。

関数semilogyを使用して結果をプロットします。グレイ符号システムは、バイナリ符号システムよりも優れたエラー レート性能を実現します。さらに、グレイ符号のエラー レートは、理論上のエラー レート統計と一致しています。

Simulink のレイズド コサイン フィルター ブロックを使用したフィルター処理

Raised Cosine Transmit Filter ブロックと Raised Cosine Receive Filter ブロックは、レイズド コサイン (RC) フィルター処理のために設計されています。各ブロックは、ルート レイズド コサイン (RRC) フィルターまたはレイズド コサイン フィルターを信号に適用できます。フィルターのロールオフ係数とスパンは可変です。

Raised Cosine Transmit Filter ブロックと Raised Cosine Receive Filter ブロックは、それぞれ送信側および受信側で使用するためにカスタマイズされています。送信フィルターは出力信号をアップサンプリング (内挿) します。受信フィルターは、入力信号がアップサンプリングされていることを想定し、構成済みのブロックの設定に基づいて、出力信号をダウンサンプリング (間引き) します。

群遅延で説明されているように、Raised Cosine Transmit Filter ブロックと Raised Cosine Receiver Filter ブロックの各々で伝播遅延が発生します。

doc_rrcfiltercompare.slx モデルは、一対のルート レイズド コサイン フィルターを使用して、送信側と受信側の間でフィルター処理を均等に分ける方法を示しています。互いに対応するルート レイズド コサイン フィルターのペアを使用することは、単一の通常のレイズド コサイン フィルターを使用することと等価です。フィルターは同じ区間を共有し、シンボルごとに同じ数のサンプルを使用しますが、上のパスの 2 つのフィルター ブロックでは平方根の形状になり、下のパスの単一のフィルター ブロックでは標準的な形状になります。

モデルを実行し、アイ ダイアグラムおよびコンスタレーション ダイアグラムを観察します。2 つの方式の性能はほぼ同じです。実際のルート レイズド コサイン フィルターはインパルス応答が制限されているため、2 つのカスケードに結合されているルート レイズド コサイン フィルターの応答と 1 つのレイズド コサイン フィルターの応答の間には、わずかな違いがあります。

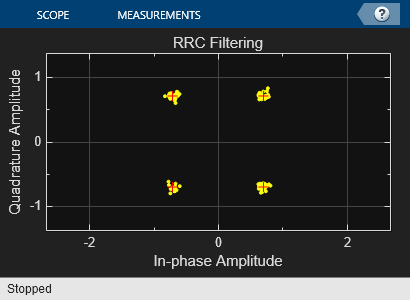
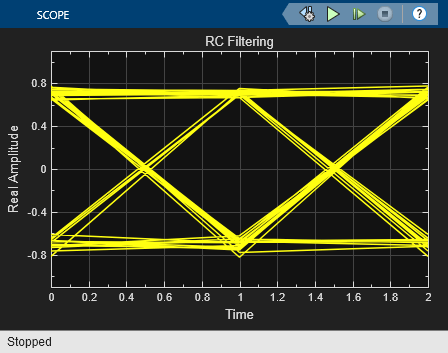
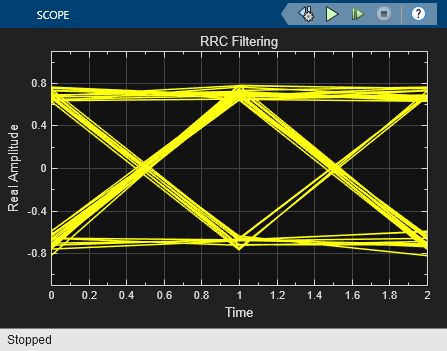
制限

• このブロックを For Each Subsystem (Simulink) で使用するには、Random number source を [グローバル ストリーム] に設定し、モデルのシミュレーション モードを [標準] または [アクセラレータ] に設定しなければなりません。これにより、実行のたびに独立したノイズ サンプルが必ず生成されます。

端子

入力

In — 入力データの信号

ベクトル | 行列

入力信号。N_S 行 1 列のベクトルまたは N_S 行 N_C 列の行列として指定します。N_S は、入力信号中のサンプルの数を示します。N_C は、チャネル数を示します。これは、入力信号行列の列数で決まります。N_S と N_C はどちらも 1 にできます。

このブロックで、長さ N_S のガウス ノイズがチャネルごとに異なる無作為の分布を使用して、それぞれの N_C チャネルに追加されます。

Var 端子が追加されるまで、この端子はブロックで名前なしになります。

データ型: double | single
複素数のサポート: あり

Var — 加法性ホワイト ガウス ノイズの分散

正のスカラー | ベクトル

加法性ホワイト ガウス ノイズの分散。正のスカラーまたは 1 行 N_C 列のベクトルとして指定します。N_C は、チャネル数を示します。これは、入力信号行列の列数で決まります。詳細については、分散の直接または間接指定を参照してください。

依存関係

この端子を有効にするには、[モード] を [分散] に設定し、[ノイズ分散ソース] を [入力端子] に設定します。

データ型: double

出力

Out — 出力データの信号

ベクトル | 行列

AWGN チャネルの出力データ信号。ベクトルまたは行列として返されます。Out のデータ型および次元は、入力信号 In のデータ型および次元と同じです。この端子はブロックで名前なしになります。

パラメーター

ブロック パラメーターを対話的に編集するには、プロパティ インスペクターを使用します。Simulink^® ツールストリップの [シミュレーション] タブの [準備] ギャラリーで [プロパティ インスペクター] を選択します。

モード — 分散モード

S/N 比 (SNR) (既定値) | Signal to noise ratio (Eb/No) | Signal to noise ratio (Es/No) | 分散

分散モード。[S/N 比 (Eb/No)]、[S/N 比 (Es/No)]、[S/N 比 (SNR)]、または [分散] として指定します。詳細は、Eb/No、Es/No、および SNR モード間の関係と分散の直接または間接指定を参照してください。

SNR (dB) — 信号強度のノイズ パワーに対する割合

10 (既定値) | スカラー | ベクトル

ノイズ パワーに対する信号強度の比 (dB 単位)。スカラーまたはベクトルで指定します。

調整可能: Yes

依存関係

このパラメーターを有効にするには、[モード] を [S/N 比 (SNR)] に設定します。

Eb/No (dB) — シンボルあたりの情報ビット エネルギーとノイズ パワー スペクトル密度の比

10 (既定値) | スカラー | ベクトル

ノイズ パワー スペクトル密度に対する、シンボルあたりの情報ビット エネルギーの比 (dB 単位)。スカラーまたはベクトルで指定します。情報ビット エネルギーは、チャネル符号化なしの振幅です。

調整可能: Yes

依存関係

このパラメーターを有効にするには、[モード] を [S/N 比 (Eb/No)] に設定します。

Es/No (dB) — シンボルあたりの情報シンボル エネルギーとノイズ パワー スペクトル密度の比

10 (既定値) | スカラー | ベクトル

ノイズ パワー スペクトル密度に対する、シンボルあたりの情報シンボル エネルギーの比 (dB 単位)。スカラーまたはベクトルで指定します。情報シンボル ビット エネルギーは、チャネル符号化なしの振幅です。

調整可能: Yes

依存関係

このパラメーターを有効にするには、[モード] を [S/N 比 (Es/No)] に設定します。

シンボルあたりのビット数 — 各入力シンボルあたりのビット数

1 (既定値) | スカラー | ベクトル

各入力シンボルあたりのビット数。スカラーまたはベクトルとして指定します。

依存関係

このパラメーターを有効にするには、[モード] を [S/N 比 (Eb/No)] に設定します。

Input signal power, referenced to 1 ohm (watts) — 入力の平均二乗電力

1 (既定値) | スカラー | ベクトル

ワット単位の入力信号の平均二乗電力。スカラーまたはベクトルで指定します。

• [モード] が [S/N 比 (Eb/No)] または [S/N 比 (Es/No)] の場合、パラメーターは入力シンボルの平均二乗電力です。

• [モード] が [S/N 比 (SNR)] の場合、このパラメーターは、入力サンプルの平均二乗電力です。

調整可能: Yes

依存関係

このパラメーターを有効にするには、[モード] を [S/N 比 (Eb/No)]、[S/N 比 (Es/No)]、または [S/N 比 (SNR)] に設定します。

Specify symbol duration in seconds — シンボルの持続時間を秒単位で指定する

off (既定値) | on

シンボルの持続時間を秒単位で指定するには、このパラメーターを選択します。

• このパラメーターを選択する場合は、[シンボル周期 (s)] パラメーターを設定し、シンボル周期を秒単位で指定します。

• このパラメーターが選択されていない場合は、[シンボルあたりのサンプル数] パラメーターを設定し、シンボルあたりのサンプル数 (サンプル単位) を指定します。

このブロックは、モデル実行時に追加するサンプル時間と適切なノイズを決定します。

詳細については、Eb/No、Es/No、および SNR モード間の関係を参照してください。

依存関係

このパラメーターを有効にするには、[モード] を [S/N 比 (Eb/No)] または [S/N 比 (Es/No)] に設定します。

シンボルあたりのサンプル数 — シンボルあたりのサンプル数

1 (既定値) | 正の整数 | 正の整数のベクトル

シンボルあたりのサンプル数 (サンプル単位)。正の整数スカラーまたはベクトルとして指定します。

依存関係

このパラメーターを有効にするには、[モード] を [S/N 比 (Eb/No)] または [S/N 比 (Es/No)] に設定し、[Specify symbol duration in seconds] は選択しません。

シンボル周期 (s) — シンボル周期 (秒単位)

[1 2 4] (既定値) | 正のスカラー | ベクトル

シンボル周期 (秒単位)。正のスカラーまたはベクトルとして指定します。このパラメーターを使用すると、このブロックは、モデル実行時に追加するサンプル時間と適切なノイズを決定します。

依存関係

このパラメーターを有効にするには、[モード] を [S/N 比 (Eb/No)] または [S/N 比 (Es/No)] に設定し、[Specify symbol duration in seconds] を選択します。

ノイズ分散ソース — Noise variance source

Parameter (既定値) | 入力端子

ノイズ分散ソース。[パラメーター] または [入力端子] として指定します。詳細については、分散の直接または間接指定を参照してください。

調整可能: Yes

依存関係

このパラメーターを有効にするには、[モード] を [分散] に設定します。

ノイズ分散 — ホワイト ガウス ノイズの分散

1 (既定値) | スカラー | ベクトル

ホワイト ガウス ノイズの分散。スカラーまたはベクトルとして指定します。詳細については、分散の直接または間接指定を参照してください。

調整可能: Yes

依存関係

この端子を有効にするには、[モード] を [分散] に設定し、[ノイズ分散ソース] を [パラメーター] に設定します。

ランダム化

乱数ソース — 乱数ソース

グローバル ストリーム (既定値) | シードあり mt19937ar

乱数ソース。[グローバル ストリーム] または [シードあり mt19937ar] として指定します。関数 parsim (Simulink) を使用する場合は、ヒントを参照してください。

初期シード — ノイズ ジェネレーター初期シード

67 (既定値) | 非負の整数

mt19937ar アルゴリズムのノイズ ジェネレーター初期シード。非負の整数として指定します。

調整可能: Yes

依存関係

このパラメーターを有効にするには、[乱数ソース] を [シードあり mt19937ar] に設定します。

シミュレーション実行方法 — 実行するシミュレーションのタイプ

コード生成 (既定値) | インタープリター型実行

実行するシミュレーションのタイプ。[コード生成] または [インタープリター型実行] として指定します。

• コード生成 — 生成された C コードを使用してモデルをシミュレートします。シミュレーションの初回実行時、Simulink は対象ブロックの C コードを生成します。このモデルは、モデルが変更されない限り以降のシミュレーションで C コードを再利用します。このオプションを使用すると、シミュレーションの起動時間は長くなりますが、以降のシミュレーションの速度は [インタープリター型実行] オプションを使用した場合よりも速くなります。

• インタープリター型実行 — MATLAB^® インタープリターを使用してモデルをシミュレートします。このオプションを使用すると、起動時間が短縮されますが、以降のシミュレーションの速度は [コード生成] オプションを使用した場合よりも遅くなります。このモードで、ブロックのソース コードをデバッグできます。

詳細については、インタープリター型実行とコード生成 (Simulink)を参照してください。

ブロックの特性

データ型	double | single
多次元信号	いいえ
可変サイズの信号	はい

ヒント

コード生成またはラピッド アクセラレーションでモンテ カルロ シミュレーションを実行する場合。関数 parsim (Simulink) を使用してモンテ カルロ シミュレーションの実行などのシミュレーションを並列で実行する場合、[乱数ソース] を [シードあり mt19937ar] に設定し、[初期シード] の値がすべてのブロックで異なっていることを確認します。

そうしないと、以下のモデル コンフィギュレーションにおいて、異なるワーカーが同じ乱数を生成する (誤解を招く結果につながる) 可能性があります。

• モデルがラピッド アクセラレータ モードである。

• このブロックで、[シミュレーション実行方法] が [コード生成] に設定されており、[乱数ソース] が [グローバル ストリーム] に設定されている。

詳細については、シミュレーション モードの選択 (Simulink)を参照してください。

アルゴリズム

Eb/No、Es/No、および SNR モード間の関係

符号化されていない複素数の入力信号の場合、AWGN Channel ブロックは次の式のとおり、E_b/N_0、E_s/N₀、および SNR と関連しています。

E_s/N₀ = (T_sym/T_samp) × SNR

E_s/N₀ = E_b/N₀ + 10log₁₀(k) in dB

• E_s は、ジュール単位の信号エネルギーを示します。

• E_b は、ジュール単位のビット エネルギーを示します。

• N₀ は、ノイズ パワー スペクトル密度 (watts/Hz) を示します。

• T_sym/T_samp は、[シンボルあたりのサンプル数] パラメーターの値と同じです。

• T_sym は、信号のシンボル周期 (秒) です。

• T_samp は、ブロックの継承されたサンプル時間 (秒) を示します。

• k は入力シンボルあたりの情報ビット数 [シンボルあたりのビット数] を示します。

実際の信号入力の場合、AWGN Channel ブロックは、次の式のとおり、E_s/N₀ および SNR と関連しています。

E_s/N₀ = 0.5 (T_sym/T_samp) × SNR

メモ

• すべての電力値は公称インピーダンス 1 オームを想定しています。

• 実数のケースの式は 2 の係数による複素数のケースに対応する式とは異なることに注意してください。特に、オブジェクトは、実数の入力信号の場合は N₀/2 watts/Hz、複素信号の場合は N₀ watts/Hz のノイズ パワー スペクトル密度を使用します。

詳細については、AWGN チャネル ノイズ レベルを参照してください。

分散の直接または間接指定

AWGN Channel によって生成されるノイズの分散を直接指定するには、[モード] を [分散] として指定します。[ノイズ分散ソース] を指定する場合、次のようにします。

• パラメーター — [ノイズ分散] パラメーターを使用して分散を正のスカラーまたはベクトルとして指定します。

• 入力端子 — Var ブロック入力を使用して分散を正のスカラーまたはベクトルとして指定します。分散入力のサンプル レートは入力信号のサンプル レートと等しくなければなりません。

分散を指定する場合、次のようになります。

• スカラーとして指定する場合、すべての信号チャネルは無相関ですが、同じ分散を共有します。

• 入力信号内のチャネル数と同じ長さのベクトルとして指定する場合、各要素は対応する信号チャネルの分散を表します。

  メモ

  複素数値の入力信号の場合、このブロックは、計算または指定された分散をもつゼロ平均複素数ガウス ノイズを追加します。複素数ノイズのそれぞれの直交成分の分散は計算または指定された値の半分です。

分散を間接的に指定する (ブロックで分散を計算する) には、次のように [モード] を指定します。

• [Signal to noise ratio (Eb/No)]、この場合ブロックはダイアログ ボックスで指定する次の数量から分散を計算します。

  • Eb/No (dB)。ビットあたりのエネルギーとノイズ パワー スペクトル密度の比率

  • シンボルあたりのビット数

  • Input signal power, referenced to 1 ohm (watts)。ブロックの入力時のシンボルの実際の強度

  • [シンボルあたりのサンプル数] または [シンボル周期 (s)]

• [Signal to noise ratio (Es/No)]、この場合ブロックはダイアログ ボックスで指定する次の数量から分散を計算します。

  • Es/No (dB)。信号エネルギーとノイズ パワー スペクトル密度の比率

  • Input signal power, referenced to 1 ohm (watts)。ブロックの入力時のシンボルの実際の強度

  • [シンボルあたりのサンプル数] または [シンボル周期 (s)]

• [Signal to noise ratio (SNR)]、この場合ブロックはダイアログ ボックスで指定する次の数量から分散を計算します。

  • SNR (dB)。信号強度のノイズ パワーに対する割合

  • Input signal power, referenced to 1 ohm (watts)。ブロックの入力時のサンプルの実際の強度

AWGN Channel ブロックでシンボル周期を変更すると、サンプルごとに加えられるノイズの分散に影響し、最終的なエラー レートが変わる原因ともなります。

$$NoiseVariance=\frac{SignalPower\times SymbolPeriod}{SampleTime\times {10}^{\frac{Es/No}{10}}}$$

ヒント

モデルのシンボル周期に等しいシンボル周期を選択します。この値は、シンボルの構成要素および適用されているオーバーサンプリングによって決まります。たとえば、シンボルは、3 ビットあり、4 でオーバーサンプリングされている場合があります。詳細については、AWGN チャネル ノイズ レベルを参照してください。

参照

[1] Proakis, John G. Digital Communications. 4th Ed. McGraw-Hill, 2001.

拡張機能

C/C++ コード生成
Simulink® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2006a より前に導入

R2025a: シンボルの持続時間を秒単位で指定する

R2025a では、このブロックに [Specify symbol duration in seconds] パラメーターが追加されました。[Specify symbol duration in seconds] を選択した場合は、[シンボル周期 (s)] パラメーターの値を指定します。このブロックは、モデル実行時に追加するサンプル時間と適切なノイズを決定します。詳細については、分散の直接または間接指定を参照してください。

R2023b: 分散の計算の更新

R2023b では、アップグレード アドバイザー (Simulink)を使用して、R2023a より前のモデルの AWGN Channel ブロックのインスタンスを更新します。R2023a の更新に加えて、これらの AWGN Channel ブロックの更新では、次のような構成になります。

• [モード] パラメーターの設定が [S/N 比 (Eb/No)] または [S/N 比 (Es/No)] であり、[Symbol period (s)] とブロック サンプル時間の組み合わせが非整数のシンボルあたりのサンプル数となる場合、[モード] はアップグレードされたブロックで [S/N 比 (SNR)] に設定されます。

• [SNR (db)] パラメーターは、適切な SNR 設定に設定されます。

R2023a では、[シンボル周期 (s)] パラメーター値とブロック サンプル時間の組み合わせが非整数のシンボルあたりのサンプル数となる場合に、アップグレード アドバイザー (Simulink)を使用して AWGN Channel ブロックを更新すると、不正確な分散値をもつノイズが生成されます。

R2023a でブロックが更新済みの場合:

1. モデルで AWGN Channel ブロックを選択します。

2. コマンド ラインで set_param(gcb,'LegacyMode','on') を実行して更新を元に戻します。

3. アップグレード アドバイザーを再実行します。

R2023a: 可変サイズのサポート

このサポートによって、シミュレーションでブロックを実行するたびに入力信号の長さを変えられるようになりました。

R2023a: 乱数発生器の更新

AWGN Channel ブロックにおいて乱数発生器 (RNG) のソースが更新され、Global stream または mt19937ar with seed を選択できるようになりました。

新しい RNG は、乱数の統計的特性が向上しています。R2023a より前に作成されたシミュレーションでは、ブロックが既定で以前の RNG (Ziggurat メソッド - V5 RANDN アルゴリズム) を使用する従来のモードになります。このモードでは、ブロックが Random Source ブロックを使用してノイズを生成します。Ziggurat メソッド (V5 RANDN アルゴリズム) を使用して、乱数が生成されます。シミュレーションを再実行するたびにブロックは同じ初期シードを再利用するため、シミュレーションを実行するたびにこのブロックは同じ信号を出力します。統計的特性を向上させるため、AWGN Channel ブロックを使用する R2023a より前のシミュレーションに対して [モデルの更新] を実行することを推奨します。

R2023a: コード生成

コード生成が既定で有効になっています。詳細については、シミュレーション実行方法を参照してください。

参考

ブロック

• Random Source | MIMO Fading Channel

オブジェクト

• comm.AWGNChannel

トピック

• 短縮、パンクチャ、および消去を使用するリード・ソロモンの例