delaunayTriangulation
2 次元および 3 次元における Delaunay 三角形分割
説明
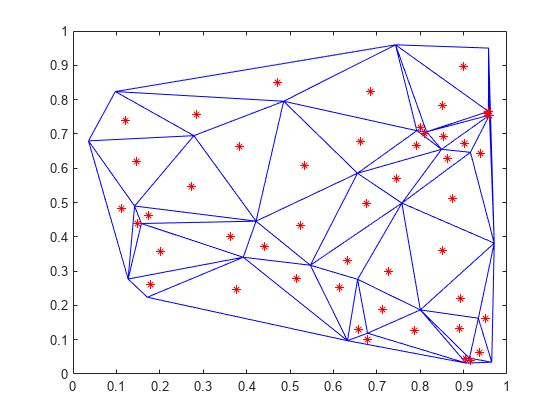
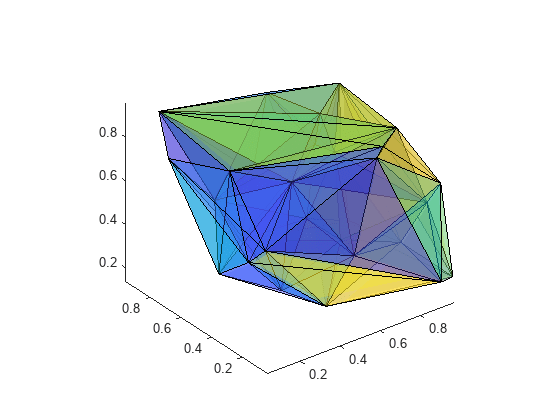
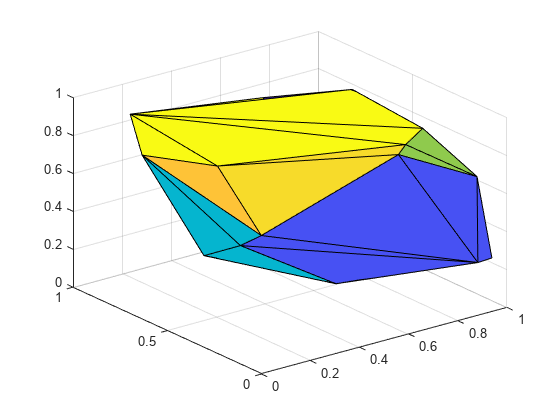
一連の点から 2 次元または 3 次元の Delaunay 三角形分割を作成するには、delaunayTriangulation オブジェクトを使用します。2 次元データでは、エッジの制約を指定することもできます。
delaunayTriangulation に対しては、triangulation クエリを含む、さまざまな幾何学的なクエリと位相幾何学的なクエリを実行できます。たとえば、特定の点を含む小平面を見つけたり、凸包の頂点を探したり、ボロノイ線図を計算したりします。
作成
delaunayTriangulation オブジェクトを作成するには、三角形分割の点と制約付きエッジを定義する入力引数を指定して、関数 delaunayTriangulation を使用します。
構文
説明
DT = delaunayTriangulation( は、P)P 内の点から Delaunay 三角形分割を作成します。点が 2 次元空間と 3 次元空間のいずれにあるかに応じて、行列 P は 2 列または 3 列です。
DT = delaunayTriangulation() は、空の Delaunay 三角形分割を作成します。
入力引数
プロパティ
オブジェクト関数
convexHull | Delaunay 三角形分割の凸包 |
isInterior | Delaunay 三角形分割の内側にあるクエリ点 |
voronoiDiagram | Delaunay 三角形分割のボロノイ線図 |
barycentricToCartesian | 座標を重心座標から直交座標に変換 |
cartesianToBarycentric | 座標を直交座標から重心座標に変換 |
circumcenter | 三角形または四面体の外心 |
edgeAttachments | 指定エッジに接続している三角形または四面体 |
edges | 三角形分割のエッジ |
faceNormal | 三角形分割の単位法線ベクトル |
featureEdges | 表面の三角形分割の鋭いエッジ |
freeBoundary | 自由境界の小平面 |
incenter | 三角形分割の要素の内心 |
isConnected | 2 つの頂点がエッジで連結されているかどうかをテスト |
nearestNeighbor | 指定の点に最も近い頂点 |
neighbors | 三角形または四面体の近傍 |
pointLocation | 三角形または四面体を囲んでいる点 |
size | 三角形分割連結リストのサイズ |
vertexAttachments | 頂点に追加された三角形または四面体 |
vertexNormal | 三角形分割の頂点法線 |
例
詳細
ヒント
delaunayTriangulationは、境界の制約が交差するかオーバーラップする場合に、不正確な結果または矛盾する結果を生成することがあります。この動作を回避するには、1 つ以上の閉じた境界を形成する、交差もオーバーラップもしない複数の制約を使用します。
拡張機能
バージョン履歴
R2013a で導入