Delaunay 三角形分割の使用

Delaunay 三角形分割の定義

Delaunay 三角形分割は、さまざまな用途の科学技術計算で幅広く使用されています。三角形分割の計算には非常に多くのアルゴリズムがありますが、中でも Delaunay 三角形分割の幾何学的な性質は非常に便利です。

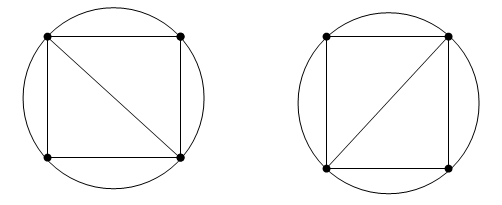
基本的な特性は Delaunay 基準です。2 次元の三角形分割の場合は、空の外接円と呼ぶことがあります。2 次元の点集合では、これらの点の Delaunay 三角形分割は各三角形の外接円が内部に他の点を含まないようにします。このプロパティは重要です。下図に示すように、T1 の外接円は空です。内部に点が含まれていません。T2 の外接円は空です。内部に点が含まれていません。この三角形分割は Delaunay 三角形分割です。

Delaunay triangulation with circumcircles plotted.

下の三角形は異なります。T1 の外接円は空ではありません。内部に V3 が含まれています。T2 の外接円は空ではありません。内部に V1 が含まれています。この三角形分割は Delaunay 三角形分割では "ありません"。

Non-Delaunay triangulation with circumcircles plotted.

空の外接円の性質を満たす時に、小さな内部角度をもつ三角形より、大きな内部角度をもつ三角形がより多く選択されるので、ドローネ三角形は “形が整っている” と言われます。非 Delaunay 三角形分割の三角形は、頂点 V2 と頂点 V4 は鋭角です。エッジ {V2, V4} が V1 と V3 が連結したエッジに置き換えられた場合には、最小角度は最大化され、Delaunay 三角形分割になります。また、Delaunay 三角形分割は最近傍の点を接続します。これら 2 つの、形が整った三角形および最近傍関係という特性は、実際面において重要な意味をもつことから、散布データの内挿には Delaunay 三角形分割が使用されます。

Delaunay プロパティを適切に設定していても三角形分割の位相幾何は、退化した点集合が存在する場合は一意ではありません。2 次元では 4 個以上の一意でない点が同一円内にある場合、退化が現れます。たとえば正方形の頂点に対する Delaunay 三角形分割は一意ではありません。

Delaunay triangulation of the vertices of a square, for which two different valid Delaunay triangulations are possible.

Delaunay 三角形分割の性質は、より高次元に拡張します。3 次元の点集合の三角形分割は四面体で構成されます。次の図は、2 つの四面体で構成された単純な 3 次元の Delaunay 三角形分割を示します。1 つの四面体の外接球は、空の外接球の基準を強調表示されています。

3-D Delaunay triangulation with circumsphere.

3 次元の Delaunay 三角形分割は、空の外接球の基準を満たす四面体を作成します。

Delaunay 三角形分割の作成

MATLAB^® には Delaunay 三角形分割を作成する 2 つの方法があります。

関数 delaunay および関数 delaunayn
delaunayTriangulation クラス

関数 delaunay は 2 次元および 3 次元の Delaunay 三角形分割をサポートします。関数 delaunayn は、4 次元以上の Delaunay 三角形分割の作成をサポートします。

ヒント

6 次元より大きい Delaunay 三角形分割の作成は、必要となるメモリが指数関数に増加するために、通常、中程度から大きな点集合に関しては実用的ではありません。

delaunayTriangulation クラスは 2 次元および 3 次元での Delaunay 三角形分割の作成をサポートしており、三角形分割に基づくアルゴリズムの開発に有用な多くのメソッドをもっています。これらのクラスメソッドは関数と似ていますが、delaunayTriangulation を使用して作成した三角形分割のみに適用できます。また、delaunayTriangulation クラスは、凸包とボロノイ線図などの関連するコンストラクターの作成をサポートしています。さらに、制約付き Delaunay 三角形分割の作成をサポートします。

概要

関数 delaunay は基本的な三角形分割データのみが必要で、そのデータがその用途に十分対応できる場合には便利です。
delaunayTriangulation クラスを使用すると、三角形分割に基づくアプリケーションの開発でさらに多くの機能が利用できます。これは、三角形分割が必要で、さらに次のいずれかの操作を実行する場合に便利です。
- クエリ点を囲む三角形または四面体の三角形分割を探索する。
- 三角形分割を使って最近傍探索を実行する。
- 三角形分割の位相学的隣接または幾何学的な性質にクエリを行う。
- 三角形分割を変更して、点を挿入または削除する。
- 三角形分割のエッジを制限する。これは制約付き Delaunay 三角形分割と呼ばれる。
- 多角形を三角形分割し、オプションで領域の外側にある三角形を削除する。
- Delaunay 三角形分割を使って、凸包またはボロノイ線図を計算する。

関数 delaunay および delaunayn の使用

関数 delaunay および delaunayn は点集合を取り、行列形式で三角形分割を作成します。このデータ構造体に関する情報は、三角形分割の行列形式を参照してください。2 次元において関数 delaunay は、散布データ点の集合によって定義される表面のプロットに利用可能な三角形分割の作成によく使われます。この用途では、このアプローチは面が一価である場合にのみ使用できることに注意してください。たとえば、単一の (x、y) 座標に対応する 2 つの z 値がある場合、球面をプロットするのに使用できません。簡単な例で、関数 delaunay でサンプルデータセットを表す面をプロットするための使用方法を示します。

この例では、関数 delaunay を使用して seamount データセットから 2 次元 Delaunay 三角形分割を作成する方法を示します。"海山 (seamount)" は水面下の山です。このデータセットは、経度 (x) と緯度 (y) による位置の集合と、それらの座標で測定された対応する海山の標高 (z) で構成されます。

seamount データセットを読み込み、(x, y) のデータを散布図として表示します。

load seamount
plot(x,y,'.','markersize',12)
xlabel('Longitude'), ylabel('Latitude')
grid on

Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains a line object which displays its values using only markers.

この点集合から Delaunay 三角形分割を作成し、triplot を使用して既存の Figure に三角形分割をプロットします。

tri = delaunay(x,y);
hold on, triplot(tri,x,y), hold off

Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains 2 objects of type line. One or more of the lines displays its values using only markers

seamount から深さのデータ (z) を追加し、頂点を持ち上げて表面を作成します。新しい Figure を作成し、trimesh を使用してワイヤーフレームモードで表面をプロットします。

figure
hidden on
trimesh(tri,x,y,z)
xlabel('Longitude'),ylabel('Latitude'),zlabel('Depth in Feet');

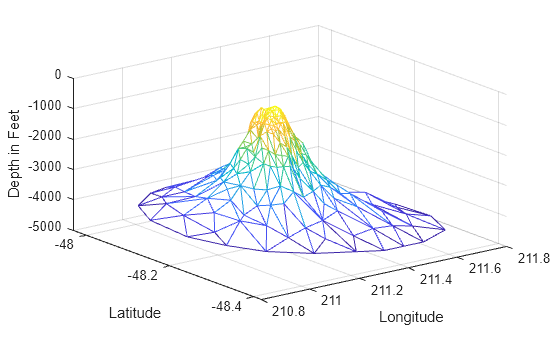
Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains an object of type patch.

表面を影付きモードでプロットする場合は、trimesh の代わりに trisurf を使用します。

3 次元 Delaunay 三角形分割は関数 delaunay を使用して作成することもできます。この三角形分割は四面体で構成されます。

この例では、ランダムデータセットの 3 次元 Delaunay 三角形分割を作成する方法を示します。三角形分割のプロットには tetramesh を使用し、FaceAlpha オプションでプロットに透明度を加えます。

rng('default')
X = rand([30 3]);
tet = delaunay(X);
faceColor  = [0.6875 0.8750 0.8984];
tetramesh(tet,X,'FaceColor', faceColor,'FaceAlpha',0.3);

Figure contains an axes object. The axes object contains 102 objects of type patch.

MATLAB には関数 delaunayn があり、4 次元以上の Delaunay 三角形分割の作成をサポートします。2 つの相補関数 tsearchn と dsearchn は、N 次元の三角形分割を空間的に探索するサポートも行います。三角形分割ベースの探索に関する詳細は、空間探索を参照してください。

delaunayTriangulation クラスの使用

MATLAB で Delaunay 三角形分割を作成するためのもう 1 つの方法として、delaunayTriangulation クラスが提供されています。delaunay と delaunayTriangulation は同じアルゴリズムに基づいて同じ三角形分割を作成しますが、delaunayTriangulation は Delaunay ベースのアルゴリズムの開発に役立つ補完的なメソッドを提供します。これらのメソッドは、三角形分割データと共にクラスと呼ばれるコンテナーにパッケージされた関数と同様です。すべてのものをクラスにまとめて保存しておくと、使いやすさを向上させるよりまとまった設定になります。点の位置および最近傍のような三角形分割ベースの探索の性能も向上します。delaunayTriangulation は、Delaunay 三角形分割のインクリメンタルな編集をサポートします。2 次元においてエッジの制約を課すこともできます。

三角形分割表現で紹介されている triangulation クラスは、2 次元と 3 次元の三角形分割に関する幾何学的なクエリと位相幾何学的なクエリをサポートしています。delaunayTriangulation は特殊な triangulation です。つまり、Delaunay 固有のクエリだけではなく、どのような triangulation クエリでも delaunayTriangulation に実行できることを意味します。より正式な MATLAB 言語の用語では、delaunayTriangulation は triangulation のサブクラスです。

この例では、delaunayTriangulation を使用して seamount のデータで Delaunay 三角形分割の作成、クエリ、編集を行う方法を示します。seamount データセットには、海山の表面を定義する位置 (x, y) と対応する標高 (z) が含まれています。

(x, y) のデータを読み込んで三角形分割します。

load seamount
DT = delaunayTriangulation(x,y)

DT = 
  delaunayTriangulation with properties:

              Points: [294x2 double]
    ConnectivityList: [566x3 double]
         Constraints: []

エッジの制約は課していないため、Constraints プロパティは空です。Points プロパティは頂点の座標を表し、ConnectivityList プロパティは三角形を表します。この 2 つのプロパティの組み合わせで三角形分割の行列データが定義されます。

delaunayTriangulation クラスは行列データをラップするラッパーで、一連の補完的なメソッドを提供します。delaunayTriangulation のプロパティには、構造体のフィールドにアクセスするのと同じ方法でアクセスできます。

頂点データにアクセスします。

DT.Points;

連結性データにアクセスします。

DT.ConnectivityList;

ConnectivityList プロパティの最初の三角形にアクセスします。

DT.ConnectivityList(1,:)

ans = 1×3

   230   205   152

delaunayTriangulation を使用すると、ConnectivityList プロパティの行列に対して簡単にインデックスを指定できます。

最初の三角形にアクセスします。

DT(1,:)

ans = 1×3

   230   205   152

最初の三角形の最初の頂点を調べます。

DT(1,1)

ans = 
230

三角形分割のすべての三角形を調べます。

DT(:,:);

delaunayTriangulation の出力 DT に対してインデックスを指定すると、delaunay から出力される三角形分割の配列に対してインデックスを指定するのと同じように機能します。この 2 つの違いは、DT に対しては追加のメソッド (たとえば nearestNeighbor や pointLocation) を呼び出せることです。

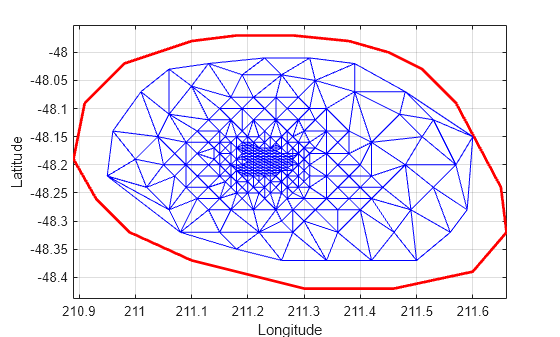
triplot を使用して delaunayTriangulation をプロットします。関数 triplot は delaunayTriangulation メソッドではありませんが、delaunayTriangulation を受け取ってプロットすることができます。

triplot(DT); 
axis equal
xlabel('Longitude'), ylabel('Latitude')
grid on

Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains an object of type line.

代わりに triplot(DT(:,:), DT.Points(:,1), DT.Points(:,2)); を使用しても同じプロットが得られます。

delaunayTriangulation のメソッド convexHull を使用して凸包を計算し、それをプロットに追加します。既に Delaunay 三角形分割があるため、このメソッドを使用することで、convhull を使用して完全な計算を行うよりも効率的に凸包が得られます。

hold on
k = convexHull(DT);
xHull = DT.Points(k,1);
yHull = DT.Points(k,2);
plot(xHull,yHull,'r','LineWidth',2); 
hold off

Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains 2 objects of type line.

delaunayTriangulation をインクリメンタルに編集して点の追加や削除を行うことができます。既存の三角形分割に点を追加する必要がある場合、拡張された点集合全体を再度三角形分割するよりもインクリメンタルに追加した方が速くなります。削除する点の数が既存の点の数と比べて相対的に少ない場合は、点をインクリメンタルに削除した方が効率的です。

三角形分割を編集して、前の計算から凸包上の点を削除します。

figure
plot(xHull,yHull,'r','LineWidth',2); 
axis equal
xlabel('Longitude'),ylabel('Latitude')
grid on

% The convex hull topology duplicates the start and end vertex.
% Remove the duplicate entry.
k(end) = [];

% Now remove the points on the convex hull.
DT.Points(k,:) = []

DT = 
  delaunayTriangulation with properties:

              Points: [274x2 double]
    ConnectivityList: [528x3 double]
         Constraints: []

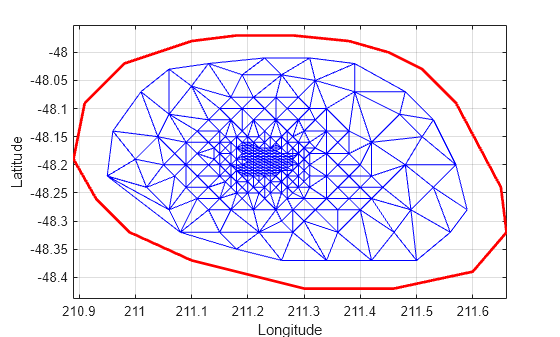
% Plot the new triangulation.
hold on
triplot(DT); 
hold off

Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains 2 objects of type line.

凸包の境界のすぐ内側に削除されなかった頂点が 1 つあります。これが包の内側にあることは、Figure でズームインツールを使って確認できます。頂点のラベルをプロットすれば、この頂点のインデックスを特定して三角形分割から削除することができます。あるいは、nearestNeighbor メソッドを使用すると、もっと簡単にインデックスを特定できます。

点は位置 (211.6, -48.15) の近くにあります。nearestNeighbor メソッドを使用して最も近い頂点を調べます。

vertexId = nearestNeighbor(DT, 211.6, -48.15)

vertexId = 
50

次に、その頂点を三角形分割から削除します。

DT.Points(vertexId,:) = []

DT = 
  delaunayTriangulation with properties:

              Points: [273x2 double]
    ConnectivityList: [525x3 double]
         Constraints: []

新しい三角形分割をプロットします。

figure
plot(xHull,yHull,'r','LineWidth',2); 
axis equal
xlabel('Longitude'),ylabel('Latitude')
grid on
hold on
triplot(DT); 
hold off

Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains 2 objects of type line.

既存の三角形分割に点を追加します。4 つの点を追加して、三角形分割を囲む四角形を形成します。

Padditional = [210.9 -48.5; 211.6 -48.5; ...
     211.6 -47.9; 210.9 -47.9];
DT.Points(end+(1:4),:) = Padditional

DT = 
  delaunayTriangulation with properties:

              Points: [277x2 double]
    ConnectivityList: [548x3 double]
         Constraints: []

既存のすべての Figure を閉じます。

close all

新しい三角形分割をプロットします。

figure
plot(xHull,yHull,'r','LineWidth',2); 
axis equal
xlabel('Longitude'),ylabel('Latitude')
grid on
hold on
triplot(DT); 
hold off

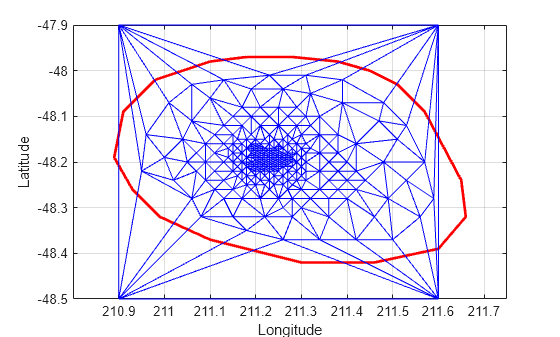
Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains 2 objects of type line.

三角形分割の点を編集して新しい位置に移動できます。追加の点集合の 1 つ目 (頂点 ID 274) を編集します。

DT.Points(274,:) = [211 -48.4];

既存のすべての Figure を閉じます。

close all

新しい三角形分割をプロットします。

figure
plot(xHull,yHull,'r','LineWidth',2); 
axis equal
xlabel('Longitude'),ylabel('Latitude')
grid on
hold on
triplot(DT); 
hold off

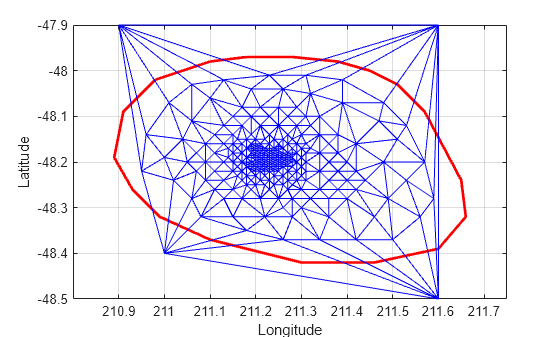
Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains 2 objects of type line.

triangulation クラスのメソッド vertexAttachments を使用して、接している三角形を調べます。頂点に接する三角形の数は可変であるため、メソッドは接している三角形の ID を cell 配列で返します。内容を抽出するには中かっこが必要です。

attTris = vertexAttachments(DT,274);
hold on
triplot(DT(attTris{:},:),DT.Points(:,1),DT.Points(:,2),'g')
hold off

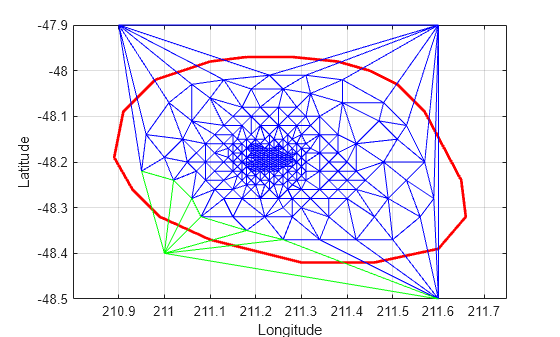
Figure contains an axes object. The axes object with xlabel Longitude, ylabel Latitude contains 3 objects of type line.

delaunayTriangulation は 3 次元空間の点の三角形分割にも使用できます。結果の三角形分割は四面体で構成されます。

この例では、delaunayTriangulation を使用して 3 次元の点の三角形分割を作成およびプロットする方法を示します。

rng('default')
P = rand(30,3);
DT = delaunayTriangulation(P)

DT = 
  delaunayTriangulation with properties:

              Points: [30x3 double]
    ConnectivityList: [102x4 double]
         Constraints: []

faceColor  = [0.6875 0.8750 0.8984];
tetramesh(DT,'FaceColor', faceColor,'FaceAlpha',0.3);

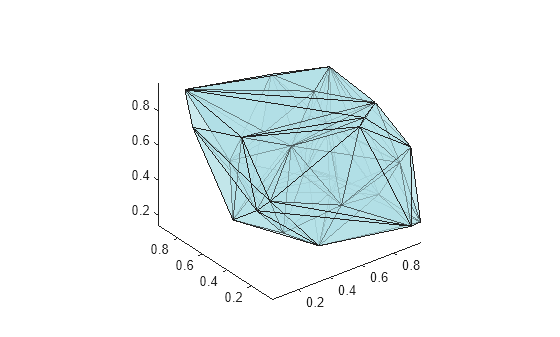
Figure contains an axes object. The axes object contains 102 objects of type patch.

関数 tetramesh は、三角形分割の内部と外部の両方の面をプロットします。大規模な 3 次元三角形分割の場合、内部の面をプロットするとリソースが不必要に使用される可能性があります。境界をプロットする方が適している場合があります。freeBoundary メソッドを使用すると、境界の三角形分割を行列形式で取得できます。その後、その結果を trimesh または trisurf に渡します。

制約付き Delaunay 三角形分割

delaunayTriangulation クラスでは 2 次元の三角形分割のエッジに制約を付けることができます。これは、三角形分割で点のペアを選択し、これらの点を連結するようエッジを制約できるということです。1 つ以上のペアの点間にエッジを強制的にプロットするようなイメージです。以下の例は、エッジの制約が三角形分割にどのような影響を与えるかを示しています。

空の外接円の基準を満たすため、以下の三角形分割は Delaunay 三角形分割となっています。

Delaunay triangulation with circumcircles plotted.

頂点 V1 と V3 の間にエッジの制約を指定して点集合を三角形分割します。

点集合を定義します。

P = [2 4; 6 1; 9 4; 6 7];

V1 と V3 の間の制約 C を定義します。

C = [1 3];
DT = delaunayTriangulation(P,C);

三角形分割をプロットし、注釈を追加します。

triplot(DT)

% Label the vertices.
hold on
numvx = size(P,1);
vxlabels = arrayfun(@(n) {sprintf('V%d', n)}, (1:numvx)');
Hpl = text(P(:,1)+0.2, P(:,2)+0.2, vxlabels, 'FontWeight', ...
  'bold', 'HorizontalAlignment','center', 'BackgroundColor', ...
  'none');
hold off


% Use the incenters to find the positions for placing triangle labels on the plot.
hold on
IC = incenter(DT);
numtri = size(DT,1);
trilabels = arrayfun(@(P) {sprintf('T%d', P)}, (1:numtri)');
Htl = text(IC(:,1),IC(:,2),trilabels,'FontWeight','bold', ...
'HorizontalAlignment','center','Color','blue');
hold off

% Plot the circumcircle associated with the triangle, T1.
hold on
[CC,r] = circumcenter(DT);
theta = 0:pi/50:2*pi;
xunit = r(1)*cos(theta) + CC(1,1);
yunit = r(1)*sin(theta) + CC(1,2);
plot(xunit,yunit,'g');
axis equal
hold off

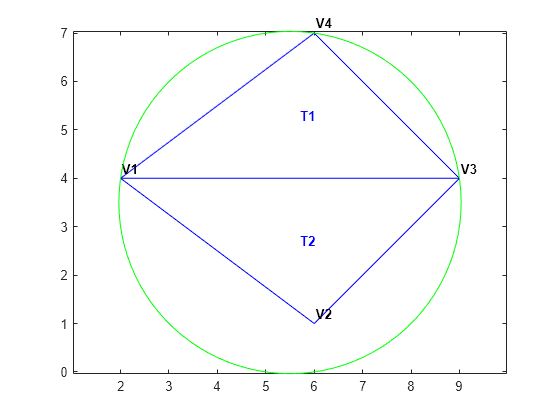
Figure contains an axes object. The axes object contains 8 objects of type line, text.

頂点間 (V1, V3) の制約は満たしていますが、Delaunay の基準が無効になっています。これにより、Delaunay 三角形分割に特有の最近傍の関係も無効になります。つまり、三角形分割に制約がある場合、delaunayTriangulation で提供される nearestNeighbor 探索メソッドがサポートされないことになります。

典型的な用途としては、三角形分割が多数の点で構成されている場合や、三角形分割の比較的少数のエッジが制約されている場合があります。このような三角形分割は、局所的に非 Delaunay であると言われます。その理由として、三角形分割内の多くの三角形が Delaunay の条件を満たしているにもかかわらず、局所的に満たさない三角形が存在する可能性があるからです。多くの用途では、空の外接円の性質に関する局所的緩和は問題になりません。

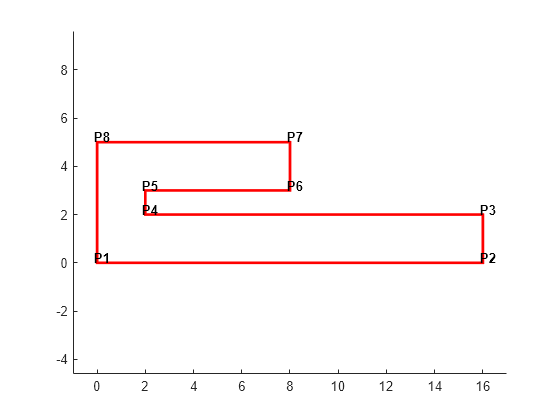
制約付き三角形分割は、一般に非凸多角形の三角形分割に使用されます。制約によって多角形のエッジと三角形分割のエッジの対応関係が得られます。この関係から、領域を表す三角形分割を抽出できます。次の例では、制約付き delaunayTriangulation を使用して非凸多角形を三角形分割する方法を示します。

多角形を定義してプロットします。

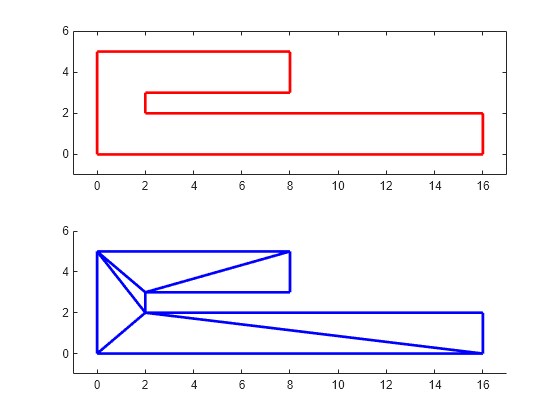
figure()
axis([-1 17 -1 6]);
axis equal
P = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5];
patch(P(:,1),P(:,2),'-r','LineWidth',2,'FaceColor',...
     'none','EdgeColor','r');
 
% Label the points.
hold on
numvx = size(P,1);
vxlabels = arrayfun(@(n) {sprintf('P%d', n)}, (1:numvx)');
Hpl = text(P(:,1)+0.2, P(:,2)+0.2, vxlabels, 'FontWeight', ...
  'bold', 'HorizontalAlignment','center', 'BackgroundColor', ...
  'none');
hold off

Figure contains an axes object. The axes object contains 9 objects of type patch, text.

三角形分割を作成し、多角形の境界と一緒にプロットします。

figure()
subplot(2,1,1);
axis([-1 17 -1 6]);
axis equal

P = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5];
DT = delaunayTriangulation(P);
triplot(DT)
hold on; 
patch(P(:,1),P(:,2),'-r','LineWidth',2,'FaceColor',...
     'none','EdgeColor','r');
hold off

% Plot the standalone triangulation in a subplot.
subplot(2,1,2);
axis([-1 17 -1 6]);
axis equal
triplot(DT)

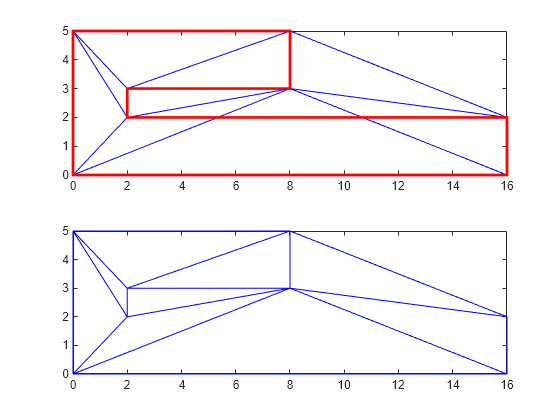
Figure contains 2 axes objects. Axes object 1 contains 2 objects of type line, patch. Axes object 2 contains an object of type line.

一部の三角形が境界をまたいでいるため、この三角形分割を使用して多角形の領域を表すことはできません。三角形分割のエッジが交差しているエッジに制約を課す必要があります。すべてのエッジが境界に沿っていなければならないため、すべてのエッジを制約する必要があります。以下の手順は、すべてのエッジを制約する方法を示したものです。

制約付きエッジの定義を入力します。制約が必要な部分 ((V1, V2)、(V2, V3) の間など) は注釈付きの Figure で確認します。

C = [1 2; 2 3; 3 4; 4 5; 5 6; 6 7; 7 8; 8 1];

一般に、多角形の境界を定義するN 個の点がシーケンスにある場合、制約は C = [(1:(N-1))' (2:N)'; N 1]; のように表すことができます。

その制約を delaunayTriangulation を作成するときに指定します。

DT = delaunayTriangulation(P,C);

あるいは、Constraints プロパティを DT.Constraints = C; のように設定することで、既存の三角形分割に制約を課すことができます。

三角形分割と多角形をプロットします。

figure('Color','white')
subplot(2,1,1);
axis([-1 17 -1 6]);
axis equal
triplot(DT)
hold on; 
patch(P(:,1),P(:,2),'-r','LineWidth',2, ...
     'FaceColor','none','EdgeColor','r'); 
hold off

% Plot the standalone triangulation in a subplot.
subplot(2,1,2);
axis([-1 17 -1 6]);
axis equal
triplot(DT)

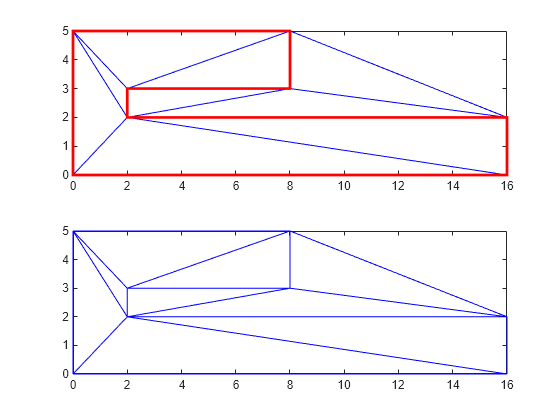
Figure contains 2 axes objects. Axes object 1 contains 2 objects of type line, patch. Axes object 2 contains an object of type line.

このプロットから、三角形分割のエッジが多角形の境界に沿っていることがわかります。ただし、凹部内に三角形分割があります。必要なのは多角形領域を表す三角形分割です。delaunayTriangulation のメソッド isInterior を使用して、多角形内にある三角形を取り除くことができます。このメソッドは、三角形が有界の幾何学的領域の内側にあるかどうかを true と false の値で示す logical 配列を返します。解析はジョルダン曲線定理に基づいて行われ、境界はエッジの制約によって定義されます。三角形分割の i 番目の三角形は、i 番目の logical フラグが true の場合は領域の内側にあると見なされ、そうでない場合は外側にあります。

ここで、isInterior メソッドを使用して、領域の三角形の集合についての計算とプロットを行います。

% Plot the constrained edges in red.
figure('Color','white')
subplot(2,1,1);
plot(P(C'),P(C'+size(P,1)),'-r','LineWidth', 2);
axis([-1 17 -1 6]);

% Compute the in/out status.
IO = isInterior(DT);
subplot(2,1,2);
hold on;
axis([-1 17 -1 6]);

% Use triplot to plot the triangles that are inside.
% Uses logical indexing and dt(i,j) shorthand
% format to access the triangulation.
triplot(DT(IO, :),DT.Points(:,1), DT.Points(:,2),'LineWidth', 2)
hold off;

Figure contains 2 axes objects. Axes object 1 contains 8 objects of type line. Axes object 2 contains an object of type line.

重複する位置を含む点集合の三角形分割

MATLAB の Delaunay アルゴリズムは、固有の点集合から三角形分割を作成します。三角形分割関数またはクラスに渡された点が固有なものでない場合、重複する位置は検出され、重複する点は無視されます。これにより、オリジナルの入力の一部の点、すなわち重複する点を参照しない三角形分割が作成されます。関数 delaunay と delaunayn を操作する場合、重複の存在は重要でなくなります。ただし、delaunayTriangulation クラスにより提供される多くのクエリはインデックスベースであるため、delaunayTriangulation では固有のデータセットを使用して、三角形分割とデータの操作が行われることに注意してください。このため、通常は固有の点集合に基づいてインデックスを指定します。このデータは delaunayTriangulation の Points プロパティにより保持されます。

次の例は、delaunayTriangulation を使用する際に、Points プロパティに格納されている固有のデータセットを参照することの重要性を示しています。

rng('default')
P = rand([25 2]);
P(18,:) = P(8,:)
P(16,:) = P(6,:)
P(12,:) = P(2,:)

DT = delaunayTriangulation(P)

この三角形分割が作成される際に、MATLAB では警告が表示されます。Points プロパティに、重複する点がデータから削除されていることが表示されます。

DT = 

  delaunayTriangulation with properties:

              Points: [22x2 double]
    ConnectivityList: [31x3 double]
         Constraints: []

たとえば、Delaunay 三角形分割が凸包を計算するために使用される場合、包の点のインデックスは固有の点集合 DT.Points に対するインデックスです。したがって、次のコードを使用して凸包の計算とプロットを行います。

K = DT.convexHull();
plot(DT.Points(:,1),DT.Points(:,2),'.');
hold on
plot(DT.Points(K,1),DT.Points(K,2),'-r');

delaunayTriangulation により提供されたインデックスと共に重複を含む元のデータセットを使用すると、結果が不正確になることがあります。delaunayTriangulation は、固有のデータセット DT.Points に基づくインデックスを使用します。たとえば、K は P に関してではなく、DT.Points に関してインデックス付けされているので、以下は不正確なプロットを作成することになります。

K = DT.convexHull();
plot(P(:,1),P(:,2),'.');
hold on
plot(P(K,1),P(K,2),'-r');

通常は delaunayTriangulation を作成する前に重複を削除して、固有のデータセットを作成した方が便利です。これを行うと混乱を避けることができます。これは、関数 unique を使用して、次のように実行することができます。

rng('default')
P = rand([25 2]);
P(18,:) = P(8,:)
P(16,:) = P(6,:)
P(12,:) = P(2,:)

[~, I, ~] = unique(P,'first','rows');
I = sort(I);
P = P(I,:);
DT = delaunayTriangulation(P)  % The point set is unique