三角形分割表現
2 次元および 3 次元領域
三角形分割はコンピューター グラフィックス、物理モデリング、地理情報システム、医療画像処理などで、2 次元と 3 次元の幾何学的領域を表現するために多くの場合使用します。地図の多角形を以下に示します。
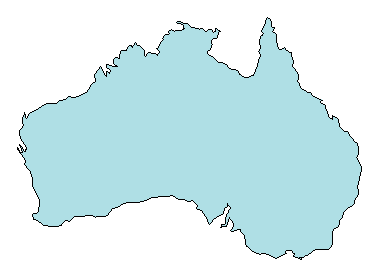
これは以下に示す地図上に三角形分割で表すことができます。
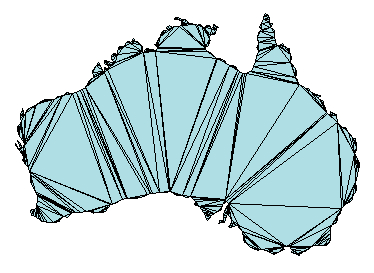
三角形分割は複雑な多角形をより簡単な三角多角形に分解します。このような多角形は、幾何学ベースのアルゴリズムまたはグラフィックス アプリケーションを開発する場合に使用することができます。
同様に、三角形分割を使用して 3 次元幾何学的領域の境界も表現することができます。以下の図は 3 次元空間における点集合の凸包を示しています。凸包の各小平面は三角形です。
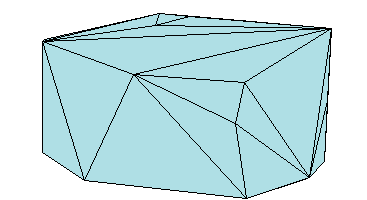
三角形分割の行列形式
MATLAB® では、三角形分割を表現するために行列形式を使用します。この形式は次の 2 つの部分で構成されます。
頂点。各行に三角形分割の点の座標が含まれる行列として表現します。
三角形分割の連結性。三角形または四面体を各行に定義した行列として表現します。
次の図に簡単な 2 次元の三角形分割を示します。
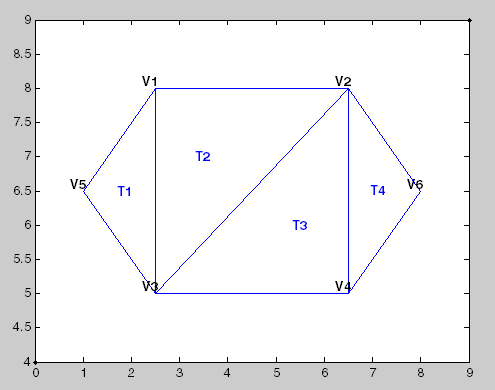
次の表に頂点の情報を示します。
| 頂点 | ||
|---|---|---|
| 頂点 ID | x 座標 | y 座標 |
| V1 | 2.5 | 8.0 |
| V2 | 6.5 | 8.0 |
| V3 | 2.5 | 5.0 |
| V4 | 6.5 | 5.0 |
| V5 | 1.0 | 6.5 |
| V6 | 8.0 | 6.5 |
上の表のデータは MATLAB 環境で行列として保存されます。頂点 ID は特定の頂点を識別するために使用するラベルです。これは頂点 ID の概念を説明するために示してありますが、明示的に保存されるわけではありません。代わりに、行列の行番号が頂点 ID として機能します。
次の表に三角形分割の連結性データを示します。
| 連結性 | |||
|---|---|---|---|
| 三角形 ID | 境界頂点の ID | ||
| T1 | 5 | 3 | 1 |
| T2 | 3 | 2 | 1 |
| T3 | 3 | 4 | 2 |
| T4 | 4 | 6 | 2 |
この表のデータは MATLAB 環境で行列として保存されます。三角形 ID は特定の三角形を識別するために使用するラベルです。これは三角形 ID の概念を説明するために示してありますが、明示的に保存されるわけではありません。代わりに、行列の行番号が三角形 ID として機能します。
三角形 T1 は 3 つの頂点 {V5, V3, V1} で定義されます。同様に、T4 は頂点 {V4, V6, V2} で定義されます。この形式は必然的に高次元でも使用できます。その場合は、データの列を追加する必要があります。たとえば、3 次元空間の四面体は、それぞれ 3 つの座標 (x、y、z) を有している 4 つの頂点で定義されます。
MATLAB を使用して、次のタイプの三角形分割を表現し、クエリすることができます。
頂点およびエッジで囲まれた三角形で構成される 2 次元の三角形分割
頂点およびエッジで囲まれた三角形で構成される 3 次元表面の三角形分割
頂点、エッジおよび面で囲まれた四面体で構成される 3 次元の三角形分割
triangulation クラスを使用した三角形分割のクエリ
行列形式を使用することにより、低水準の配列に基づいてコンパクトに三角形分割を表現できます。三角形分割をアルゴリズムの開発に使用する場合、幾何学的な性質、トポロジおよび隣接情報についての詳細が必要なことがあります。
たとえば、下記に示す注釈付きの三角形分割をプロットする前に、三角形の内心点を計算する場合があります。この場合、内心点を使用して、三角形のラベル (T1、T2 など) をそれぞれの三角形内に表示することができます。境界線を赤でプロットする場合は、1 つの三角形のみで参照されているエッジを特定する必要があります。
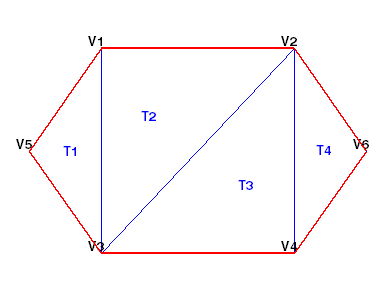
triangulation クラス
triangulation を使用すると、関数 delaunay や他のソフトウェア ツールからの行列出力など、行列形式をもつ 2 次元または 3 次元の三角形分割データのインメモリ表現を作成することができます。triangulation を使用してデータを表現する場合、幾何学的なクエリと位相幾何学的なクエリを実行することができます。これは、幾何学的なアルゴリズムを開発する際に使用できます。たとえば、ある頂点に接続されている三角形や四面体、あるエッジを共有するそれらの図形、その外心、およびその他の特徴をクエリすることができます。
次の 2 つの方法のいずれかで triangulation を作成することができます。
行列形式の既存のデータを
triangulationに渡します。delaunayやconvhullなどの MATLAB 関数の出力をこのデータとして使用することができます。また、別のソフトウェア アプリケーションで作成された三角形分割データをインポートすることもできます。インポート データで作業する場合は、0 ベースではなく、1 ベースのインデックスを使用して、連結性データが頂点配列を参照することを確認する必要があります。delaunayTriangulationに点集合を渡します。出力される Delaunay 三角形分割は、特殊なtriangulationです。つまり、Delaunay 固有のクエリだけではなく、どのようなtriangulationクエリでもデータに実行できることを意味します。より正式な MATLAB 言語の用語では、delaunayTriangulationはtriangulationのサブクラスです。
行列データから三角形分割を作成
この例では、三角形分割行列データを使用して三角形分割を作成し、その概要と使用方法を調べる方法を説明します。
頂点データを含む行列 P を作成します。
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];連結性 T を定義します。
T = [5 3 1;
3 2 1;
3 4 2;
4 6 2];このデータから、triangulation を作成します。
TR = triangulation(T,P)
TR =
triangulation with properties:
Points: [6×2 double]
ConnectivityList: [4×3 double]
struct のフィールドにアクセスするのと同じ方法で、triangulation のプロパティにアクセスします。たとえば、各頂点の座標が含まれる Points プロパティを調べます。
TR.Points
ans = 6×2
2.5000 8.0000
6.5000 8.0000
2.5000 5.0000
6.5000 5.0000
1.0000 6.5000
8.0000 6.5000
次に、連結性を調べます。
TR.ConnectivityList
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
Points プロパティと ConnectivityList プロパティによって三角形分割の行列データを定義します。
triangulation クラスは行列データをラップするラッパーです。ただし、本当の利点は triangulation クラス メソッドの有用性にあります。このメソッドは、triangulation や他の関連入力データを受け取る関数のようなものです。
triangulation クラスを使用すると、ConnectivityList プロパティ行列に対してインデックスを簡単に指定できます。三角形分割の最初の三角形にアクセスします。
TR.ConnectivityList(1,:)
ans = 1×3
5 3 1
最初の三角形を取得するには、TR(1,:) を使用する方法もあります。
最初の三角形の最初の頂点を調べます。
TR(1,1)
ans = 5
最初の三角形の 2 番目の頂点を調べます。
TR(1,2)
ans = 3
次に、三角形分割内のすべての三角形を調べます。
TR(:,:)
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
triplot を使用して triangulation をプロットします。関数 triplot は triangulation メソッドではありませんが、triangulation を受け取ってプロットすることができます。
figure
triplot(TR)
axis equal
triangulation メソッド freeBoundary を使用し、自由境界をクエリして、プロットでそれを強調表示します。このメソッドは、1 つの三角形のみで共有される三角形分割のエッジを返します。返されたエッジは頂点 ID で表現されます。
boundaryedges = freeBoundary(TR)';
次に、赤線で境界のエッジをプロットします。
hold on plot(P(boundaryedges,1),P(boundaryedges,2),'-r','LineWidth',2) hold off

freeBoundary メソッドは三角形分割の検証に使用できます。たとえば、三角形分割の内部に赤のエッジが見られる場合は、三角形の連結方法に問題があることがわかります。
delaunayTriangulation を使用して三角形分割を作成
この例では、delaunayTriangulation を使用して Delaunay 三角形分割を作成する方法を示します。
delaunayTriangulation クラスを使用して Delaunay 三角形分割を作成する場合、delaunayTriangulation は triangulation のサブクラスであるため、triangulation メソッドに自動的にアクセスできます。
delaunayTriangulation を点集合から作成します。
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
DT = delaunayTriangulation(P)DT =
delaunayTriangulation with properties:
Points: [6×2 double]
ConnectivityList: [4×3 double]
Constraints: []
出力される delaunayTriangulation オブジェクトには、triangulation オブジェクトと同様に、Points プロパティと ConnectivityList プロパティが含まれています。
triangulation と同様に、三角形分割へのアクセスには直接インデックスを使用します。たとえば、最初の三角形の連結性を調べます。
DT(1,:)
ans = 1×3
5 3 1
次に、三角形分割全体の連結性を調べます。
DT(:,:)
ans = 4×3
5 3 1
3 4 1
1 4 2
2 4 6
関数 triplot を使用して三角形分割をプロットします。
triplot(DT)
axis equal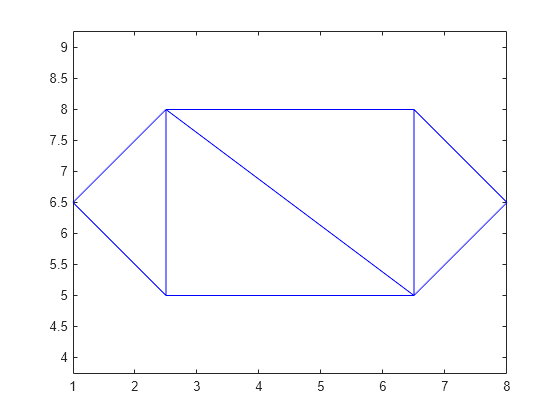
親クラス triangulation には incenter メソッドがあり、各三角形の内心点を計算できます。
IC = incenter(DT)
IC = 4×2
1.8787 6.5000
3.5000 6.0000
5.5000 7.0000
7.1213 6.5000
戻り値 IC は三角形の内心点を表す座標の配列です。
次に、内心点を使用して、プロットに三角形のラベルを配置する位置を見つけます。
hold on numtri = size(DT,1); trilabels = arrayfun(@(P) {sprintf('T%d', P)}, (1:numtri)'); Htl = text(IC(:,1),IC(:,2),trilabels,'FontWeight','bold', ... 'HorizontalAlignment','center','Color','blue'); hold off
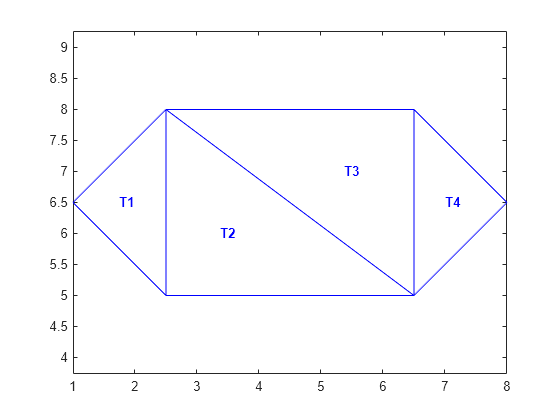
delaunayTriangulation で Delaunay 三角形分割を作成する代わりに、関数 delaunay を使用して、三角形分割の連結性データを作成し、その連結性データを triangulation に渡すこともできます。以下に例を示します。
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
T = delaunay(P);
TR = triangulation(T,P);
IC = incenter(TR);この例ではどちらの方法も有効ですが、Delaunay 三角形分割を作成し、それに対してクエリを実行する場合は、次の理由から delaunayTriangulation を使用してください。
delaunayTriangulationクラスには三角形分割を操作する場合に役立つメソッドが他にもあります。たとえば、最近傍探索や point-in-triangle 探索を実行できます。点を追加、移動または削除するために、三角形分割を編集することができます。
制約付き Delaunay 三角形分割も作成できます。これにより、2 次元領域の三角形分割を作成することができます。
参考
delaunay | delaunayTriangulation | freeBoundary | triangulation | triplot