空間探索

はじめに

MATLAB® は、Delaunay 三角形分割または一般的な三角形分割を使用して空間探索に必要な関数を提供します。MATLAB がサポートする検索クエリは以下のとおりです。

• 最近傍探索 (最近点探索または近接探索とも呼ばれます)。

• 点の位置探索 (しばしば三角形内の point-in-triangle 探索、またはシンプレックス内の点探索と呼ばれ、ここではシンプレックスは三角形、四面体またはより高い次元に相当するものです)。

ユークリッド空間の点集合 X およびクエリ点 q を作成する場合、最近傍探索は、X 内の他の点に比べて q により近い X 内の点 p を探索します。X の三角形分割を作成する場合、点の位置探索はクエリ点 q を含む三角形または四面体を探索します。これらのメソッドは Delaunay と一般的な三角形分割の両方に有効であるため、点の変更が Delaunay の基準に反する場合にも使用できます。行列形式で表現されている一般的な三角形分割を探索することもできます。

MATLAB は N 次元での探索スキームをサポートしますが、通常は次元数が 3 次元を超えると正確な空間探索はできなくなります。10 次元までの大規模な問題に対する近似代替方法を考えなければなりません。

最近傍探索

問題の次元によって、MATLAB での最近傍を計算する方法がいくつかあります。

• 2 次元探索および 3 次元探索では、triangulationクラスにより提供され、delaunayTriangulationクラスにより継承されているnearestNeighborメソッドを使用します。

• 4 次元以上では関数delaunaynを使って、探索を実行するための三角形分割および相補関数dsearchnを作成します。これらの N 次元関数は 2 次元および 3 次元をサポートしていますが、三角形分割探索メソッドほど一般的でも効率的でもありません。

この例では、delaunayTriangulation を使用して 2 次元で最近傍探索を実行する方法を説明します。

まず、15 個の点からなるランダムな集合を作成します。

X = [3.5 8.2; 6.8 8.3; 1.3 6.5; 3.5 6.3; 5.8 6.2; 8.3 6.5;...
    1 4; 2.7 4.3; 5 4.5; 7 3.5; 8.7 4.2; 1.5 2.1; 4.1 1.1; ...
    7 1.5; 8.5 2.75];

点をプロットし、ID ラベルを示す注釈を追加します。

plot(X(:,1),X(:,2),'ob')
hold on
vxlabels = arrayfun(@(n) {sprintf('X%d', n)}, (1:15)');
Hpl = text(X(:,1)+0.2, X(:,2)+0.2, vxlabels, 'FontWeight', ...
    'bold', 'HorizontalAlignment','center', 'BackgroundColor', ...
    'none');
hold off

点から Delaunay 三角形分割を作成します。

dt = delaunayTriangulation(X);

いくつかのクエリ点を作成し、各クエリ点について、対応する X 内の最近傍のインデックスを nearestNeighbor メソッドを使用して求めます。

numq = 10;
rng(0,'twister');
q = 2+rand(numq,2)*6;
xi = nearestNeighbor(dt, q);

クエリ点をプロットに追加し、線分を追加してクエリ点を最近傍に結合します。

xnn = X(xi,:);

hold on
plot(q(:,1),q(:,2),'or');
plot([xnn(:,1) q(:,1)]',[xnn(:,2) q(:,2)]','-r');

vxlabels = arrayfun(@(n) {sprintf('q%d', n)}, (1:numq)');
Hpl = text(q(:,1)+0.2, q(:,2)+0.2, vxlabels, 'FontWeight', ...
    'bold', 'HorizontalAlignment','center', ...
    'BackgroundColor','none');

hold off

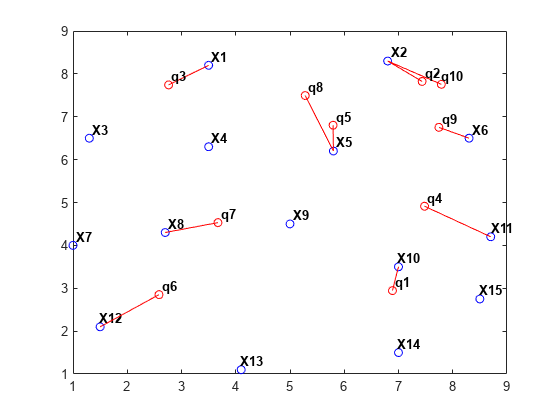
3 次元での最近傍探索の実行は、delaunayTriangulation に基づいた 2 次元の例を直接拡張したものです。

4 次元以上では、次の例の中で示すように関数 delaunayn と関数 dsearchn を使用します。

4 次元に無作為な点のサンプルを作成し、delaunayn を使って点を三角形分割します。

X = 20*rand(50,4) -10;
tri = delaunayn(X);

いくつかのクエリ点を作成し、関数 dsearchn を使って X の各クエリ点に対応する最近傍のインデックスを求めます。

q = rand(5,4);
xi = dsearchn(X,tri, q);

nearestNeighbor メソッドおよび関数 dsearchn により、クエリ点と最近傍間のユークリッド距離をオプションの引数として返すことができます。4 次元の例では、距離 dnn は以下のように計算することができます。

[xi,dnn] = dsearchn(X,tri,q);

点の位置探索

点の位置探索は、クエリ点を囲むシンプレックス (三角形、四面体など) を探索する三角形分割探索アルゴリズムです。最近傍探索の場合のように、問題の次元によって、MATLAB における点の位置探索を実行するアプローチがいくつかあります。

• 2 次元および 3 次元では、triangulation クラスにより提供され、delaunayTriangulation クラスにより継承されているpointLocationメソッドによるクラスベースのアプローチを使います。

• 4 次元以上では関数 delaunayn を使って、点の位置探索を実行するための三角形分割および相補関数tsearchnを作成します。これらの N 次元関数は 2 次元および 3 次元をサポートしていますが、三角形分割探索メソッドほど一般的でも効率的でもありません。

この例では、delaunayTriangulation クラスを使用して 2 次元で点の位置探索を実行する方法を説明します。

まず、2 次元の点の集合を作成します。

X = [3.5 8.2; 6.8 8.3; 1.3 6.5; 3.5 6.3; 5.8 6.2; ...
    8.3 6.5; 1 4; 2.7 4.3; 5 4.5; 7 3.5; 8.7 4.2; ...
    1.5 2.1; 4.1 1.1; 7 1.5; 8.5 2.75];

三角形分割を作成してプロットし、三角形の内心に三角形 ID ラベルを表示します。

dt = delaunayTriangulation(X);
triplot(dt);

hold on
ic = incenter(dt);
numtri = size(dt,1);
trilabels = arrayfun(@(x) {sprintf('T%d', x)}, (1:numtri)');
Htl = text(ic(:,1), ic(:,2), trilabels, 'FontWeight', ...
      'bold', 'HorizontalAlignment', 'center', 'Color', ...
      'blue');
hold off

ここで、クエリ点をいくつか作成し、プロットに追加します。次に、pointLocation メソッドを使用して、それらを囲む対応する三角形のインデックスを見つけます。

q = [5.9344    6.2363;
    2.2143    2.1910;
    7.0948    3.6615;
    7.6040    2.2770;
    6.0724    2.5828;
    6.5464    6.9407;
    6.4588    6.1690;
    4.3534    3.9026;
    5.9329    7.7013;
    3.0271    2.2067];

hold on; 
plot(q(:,1),q(:,2),'*r'); 
vxlabels = arrayfun(@(n) {sprintf('q%d', n)}, (1:10)');
Hpl = text(q(:,1)+0.2, q(:,2)+0.2, vxlabels, 'FontWeight', ...
    'bold', 'HorizontalAlignment','center', ... 
    'BackgroundColor', 'none');
hold off

ti = pointLocation(dt,q);

3 次元での点の位置探索の実行は、delaunayTriangulation を使用した 2 次元での点の位置探索の実行を直接拡張したものです。

4 次元以上では、次の例の中で示すように関数 delaunayn と関数 tsearchn を使用します。

4 次元に無作為な点のサンプルを作成し、delaunayn を使って点を三角形分割します。

X = 20*rand(50,4) -10;
tri = delaunayn(X);

いくつかのクエリ点を作成し、関数 tsearchn を使って、それらを囲む対応するシンプレックスのインデックスを求めます。

q = rand(5,4);
ti = tsearchn(X,tri,q);

pointLocation メソッドと関数 tsearchn により、対応する重心座標をオプションの引数として返すことができます。4 次元の例では、重心座標は以下のように計算することができます。

[ti,bc] = tsearchn(X,tri,q);

重心座標は、線形内挿を実行する時に便利です。これらの座標によって、囲まれているシンプレックスの各頂点の値を計るために使用できる重みが提供されます。詳細については、散布データの内挿を参照してください。

参考

nearestNeighbor | delaunayTriangulation | triangulation | delaunayn | dsearchn | pointLocation | triangulation | tsearchn | delaunay

関連するトピック

• Delaunay 三角形分割の使用
• 三角形分割表現
• 散布データの内挿