散布データの内挿
散布データ
散布データは点集合 X と対応する値 V で構成されており、各点の相対的位置関係には体系や秩序は存在しません。散布データを内挿するためのアプローチはさまざまです。広く使われているアプローチの 1 つは、点の Delaunay 三角形分割を使用します。
この例では、点を三角形分割してから、大きさ V を使用して X と直交する次元に頂点を持ち上げることによって内挿表面を作成する方法を示します。
このアプローチを適用する方法にはいくつかのバリエーションがあります。この例では別々の手順に分けて内挿を行っていますが、通常は内挿プロセス全体を 1 つの関数呼び出しで実行できます。
放物面の表面の散布データ セットを作成します。
X = [-1.5 3.2; 1.8 3.3; -3.7 1.5; -1.5 1.3; ... 0.8 1.2; 3.3 1.5; -4.0 -1.0; -2.3 -0.7; 0 -0.5; 2.0 -1.5; 3.7 -0.8; -3.5 -2.9; ... -0.9 -3.9; 2.0 -3.5; 3.5 -2.25]; V = X(:,1).^2 + X(:,2).^2; hold on plot3(X(:,1),X(:,2),zeros(15,1), '*r') axis([-4, 4, -4, 4, 0, 25]); grid stem3(X(:,1),X(:,2),V,'^','fill') hold off view(322.5, 30);

Delaunay 三角形分割を作成し、頂点を持ち上げて、クエリ点 Xq で内挿を評価します。
figure('Color', 'white') t = delaunay(X(:,1),X(:,2)); hold on trimesh(t,X(:,1),X(:,2), zeros(15,1), ... 'EdgeColor','r', 'FaceColor','none') defaultFaceColor = [0.6875 0.8750 0.8984]; trisurf(t,X(:,1),X(:,2), V, 'FaceColor', ... defaultFaceColor, 'FaceAlpha',0.9); plot3(X(:,1),X(:,2),zeros(15,1), '*r') axis([-4, 4, -4, 4, 0, 25]); grid plot3(-2.6,-2.6,0,'*b','LineWidth', 1.6) plot3([-2.6 -2.6]',[-2.6 -2.6]',[0 13.52]','-b','LineWidth',1.6) hold off view(322.5, 30); text(-2.0, -2.6, 'Xq', 'FontWeight', 'bold', ... 'HorizontalAlignment','center', 'BackgroundColor', 'none');
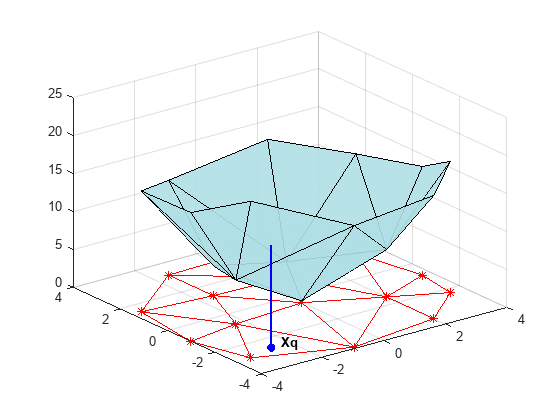
通常、この手順では、クエリ点を囲む三角形を見つけ出すために三角形分割のデータ構造の走査を行います。点を見つけた後に値を計算する手順は内挿法によって異なります。近傍の最も近い点を計算し、その点の値を使用することができます (最近傍内挿法)。また、点を囲む三角形の 3 つの頂点から、その重み付き和を計算することもできます (線形内挿法)。これらの手法とそのバリエーションについて、散布データの内挿の説明とリファレンスで取り上げています。
この図は 2 次元内挿を強調表示したものですが、この手法はより高次元に適用できます。より一般的には、与えられた点集合 X と対応する値 V から、V = F(X) の形式の内挿を作成できます。クエリ点 Xq で内挿を評価することで Vq = F(Xq) が得られます。これは一価関数であり、X の凸包内の任意のクエリ点 Xq に対して、一意の値 Vq を生成します。十分な内挿が得られるように、サンプル データはこの特性を満たしているものとします。
MATLAB® は、三角形分割に基づいて散布データを内挿する 2 つの方法を提供します。
関数 griddata は、2 次元散布データの内挿をサポートしています。関数 griddatan は、N 次元の散布データの内挿をサポートします。しかし 6 次元を超える場合、基底にある三角形分割が必要とするメモリが指数関数的に増大するため、大量の点集合の管理には向きません。
scatteredInterpolant クラスは、2 次元と 3 次元空間で分散データの内挿をサポートします。より効率的という理由で、このクラスの使用が推奨され、既に、より幅広い内挿問題に適用されています。
griddata と griddatan を使った散布データの内挿
関数 griddata と griddatan は、サンプル点の集合 X、対応する値 V およびクエリ点 Xq を取得して、内挿した値 Vq を返します。呼び出し構文は各関数で似ています。違いは 2 次元/3 次元の関数 griddata で X、Y/X、Y、Z 座標で点を定義できる点です。これら 2 つの関数は、定義済みのグリッド ポイントの位置で散布データを内挿します。これらの目的はグリッド データの作成であり、名称はここから来ています。内挿は、実際にはかなり一般的です。点の凸包内の任意の位置でクエリを行う場合もあります。
この例では、関数 griddata がグリッド点の集合において散布データをどのように内挿し、そのグリッド データを使用して等高線図をどのように作成するかを示します。
seamount データ セットをプロットします。"海山 (seamount)" は水面下の山です。このデータ セットは、経度 (x) と緯度 (y) による位置の集合と、それらの座標で測定された対応する seamount の標高 (z) で構成されます。
load seamount plot3(x,y,z,'.','markersize',12) xlabel('Longitude') ylabel('Latitude') zlabel('Depth in Feet') grid on

meshgrid を使用して、緯度と経度の平面で 2 次元グリッド点の集合を作成し、その後、griddata を使用して、それらの点の対応する深さを内挿します。
figure [xi,yi] = meshgrid(210.8:0.01:211.8, -48.5:0.01:-47.9); zi = griddata(x,y,z,xi,yi); surf(xi,yi,zi); xlabel('Longitude') ylabel('Latitude') zlabel('Depth in Feet')

これでデータがグリッド形式になったので、等高線を計算してプロットします。
figure [c,h] = contour(xi,yi,zi); clabel(c,h); xlabel('Longitude') ylabel('Latitude')

また、griddata を使って、データセットの凸包内の任意の位置で内挿することができます。たとえば、座標 (211.3, -48.2) で深さが以下のように計算されます。
zi = griddata(x,y,z, 211.3, -48.2);
基本的な三角形分割は、関数 griddata が呼び出されるたびに計算されます。同じデータ セットが異なるクエリ点で繰り返し内挿される場合、性能に影響を与えます。scatteredInterpolant クラスを使った散布データの内挿で説明されている scatteredInterpolant クラスは、この点でより効率的です。
また、MATLAB ソフトウェアは、griddatan を提供して、高次元の内挿をサポートしています。呼び出し構文は、griddata と類似しています。
scatteredInterpolant クラス
関数 griddata は、事前定義されたグリッド ポイント位置の集合での値を見つけるために内挿が必要な場合、有効です。実際には、多くの内挿問題はより一般的で、scatteredInterpolant クラスによって、より大きな柔軟性が提供されます。クラスには次の利点があります。
それは、効率的なクエリが可能な内挿関数を作成します。つまり、基本的な三角形分割が一度作成され、次のクエリに再使用されます。
内挿法は、三角形分割とは無関係に変更することができます。
データ点での値は、三角形分割と関係なく変更することができます。
データ点は、完全な再計算をトリガーしないで既存の内挿に徐々に追加することができます。編集される点の数量がサンプル点の全数に対して相対的に小さい場合、データ点は効率的に削除、移動することができます。
これは、凸包の外部の点における値を近似する外挿機能を提供します。詳細は、散布データの外挿を参照してください。
scatteredInterpolant は、次の内挿法を提供します。
'nearest'— 最近傍による内挿。内挿する曲面は不連続です。'linear'— 線形内挿 (既定の設定)。内挿する曲面は C0 連続です。'natural'— 自然な近傍内挿。内挿する曲面はサンプル点を除き C1 連続です。
scatteredInterpolant クラスは、2 次元と 3 次元空間で分散データの内挿をサポートします。scatteredInterpolant を呼び出し、点の位置と対応する値、およびオプションで内挿法と外挿法を渡すことで、内挿を作成できます。scatteredInterpolant を作成して評価する際に使用できる構文の詳細については、scatteredInterpolant のリファレンス ページを参照してください。
scatteredInterpolant クラスを使った散布データの内挿
この例では、scatteredInterpolant を使用して関数 peaks の散布サンプリングを内挿する方法を説明します。
散布データ セットを作成します。
rng default;
X = -3 + 6.*rand([250 2]);
V = peaks(X(:,1),X(:,2));内挿を作成します。
F = scatteredInterpolant(X,V)
F =
scatteredInterpolant with properties:
Points: [250×2 double]
Values: [250×1 double]
Method: 'linear'
ExtrapolationMethod: 'linear'
Points プロパティはデータ点の座標を示し、Values プロパティはこれに関連付けられた値を示します。Method プロパティは内挿を実行する内挿法を示します。ExtrapolationMethod プロパティはクエリ点が凸包の外にある場合に使用される外挿法を示します。
F のプロパティに、struct のフィールドにアクセスするのと同じ方法でアクセスできます。たとえば、F.Points を使用して、データ点の座標を調べます。
内挿を評価します。
scatteredInterpolant は、内挿に添字付き評価を提供します。それは、関数と同じ方法で評価されます。以下のように内挿を評価できます。この場合、クエリ位置の値は、Vq で計算されます。単一のクエリ点で評価できます。
Vq = F([1.5 1.25])
Vq = 1.4838
また、個々の座標を渡すことができます。
Vq = F(1.5, 1.25)
Vq = 1.4838
点の位置のベクトルで評価できます。
Xq = [0.5 0.25; 0.75 0.35; 1.25 0.85]; Vq = F(Xq)
Vq = 3×1
0.4057
1.2199
2.1639
グリッド点の位置で F を評価して、その結果をプロットすることができます。
[Xq,Yq] = meshgrid(-2.5:0.125:2.5); Vq = F(Xq,Yq); surf(Xq,Yq,Vq); xlabel('X','fontweight','b'), ylabel('Y','fontweight','b'); zlabel('Value - V','fontweight','b'); title('Linear Interpolation Method','fontweight','b');

内挿法を変更します。
内挿法は実行中に変更できます。メソッドを 'nearest' に設定します。
F.Method = 'nearest';前述したように、内挿を再評価し、プロットします。
Vq = F(Xq,Yq); figure surf(Xq,Yq,Vq); xlabel('X','fontweight','b'),ylabel('Y','fontweight','b') zlabel('Value - V','fontweight','b') title('Nearest neighbor Interpolation Method','fontweight','b');

内挿法を自然の近傍に変更し、結果の再評価とプロットを行います。
F.Method = 'natural'; Vq = F(Xq,Yq); figure surf(Xq,Yq,Vq); xlabel('X','fontweight','b'),ylabel('Y','fontweight','b') zlabel('Value - V','fontweight','b') title('Natural neighbor Interpolation Method','fontweight','b');

サンプル データ位置で値を置き換えます。
値 V は、実行中にサンプル データ位置 X で変更することができます。いくつかの内挿の問題は同じ位置に複数の値のセットをもつ可能性があるため、この機能は、実際のところ便利です。たとえば、位置 (x,y,z) と対応する成分を含む速度ベクトル (Vx,Vy, Vz) によって定義される 3 次元速度フィールドを内挿すると仮定します。それぞれの速度成分を値のプロパティ (V) に順に代入して、内挿することができます。これにより、重要なパフォーマンス上のメリットが生まれます。毎回新たに内挿を計算する手間を省いて、同じ内挿を再利用できるためです。
次のステップでは、例における値の変更方法を示します。式 を使って値を計算します。
V = X(:,1).*exp(-X(:,1).^2-X(:,2).^2); F.Values = V;
内挿を評価して、結果をプロットします。
Vq = F(Xq,Yq); figure surf(Xq,Yq,Vq); xlabel('X','fontweight','b'), ylabel('Y','fontweight','b') zlabel('Value - V','fontweight','b') title('Natural neighbor interpolation of v = x.*exp(-x.^2-y.^2)')

追加の点の位置と既存の内挿の値を追加します。
これは、拡張データ セットを使って、完全な再計算と異なり効率的な更新を実行します。
サンプル データを追加する場合、点の位置と対応する値の両方を追加することが重要です。
例を続けて、以下のような新しいサンプル点を作成します。
X = -1.5 + 3.*rand(100,2); V = X(:,1).*exp(-X(:,1).^2-X(:,2).^2);
新しい点と対応する値を、三角形分割に追加します。
F.Points(end+(1:100),:) = X; F.Values(end+(1:100)) = V;
絞り込まれた内挿を評価して、結果をプロットします。
Vq = F(Xq,Yq); figure surf(Xq,Yq,Vq); xlabel('X','fontweight','b'), ylabel('Y','fontweight','b'); zlabel('Value - V','fontweight','b');

データを内挿から削除します。
サンプル データ点を段階的に内挿から削除することができます。また、データ点とそれに対応する値を内挿から削除することもできます。これは、疑似的な外れ値を削除するのに役立ちます。
サンプル データを削除する場合、点の位置とそれに対応する値の両方を削除することが重要です。
25 番目の点を削除します。
F.Points(25,:) = []; F.Values(25) = [];
点 5 から 15 を削除します。
F.Points(5:15,:) = []; F.Values(5:15) = [];
150 点を保持し、残りを削除します。
F.Points(150:end,:) = []; F.Values(150:end) = [];
次のように評価およびプロットすると、粗い曲面が作成されます。
Vq = F(Xq,Yq); figure surf(Xq,Yq,Vq); xlabel('X','fontweight','b'), ylabel('Y','fontweight','b'); zlabel('Value - V','fontweight','b'); title('Interpolation of v = x.*exp(-x.^2-y.^2) with sample points removed')

複素数散布データの内挿
この例では、各サンプル位置における値が複素数の場合に散布データを内挿する方法を示します。
サンプル データを作成します。
rng('default')
X = -3 + 6*rand([250 2]);
V = complex(X(:,1).*X(:,2), X(:,1).^2 + X(:,2).^2);内挿を作成します。
F = scatteredInterpolant(X,V);
クエリ点のグリッドを作成し、グリッド点で内挿を評価します。
[Xq,Yq] = meshgrid(-2.5:0.125:2.5); Vq = F(Xq,Yq);
Vq の実数部をプロットします。
VqReal = real(Vq); figure surf(Xq,Yq,VqReal); xlabel('X'); ylabel('Y'); zlabel('Real Value - V'); title('Real Component of Interpolated Value');

Vq の虚数部をプロットします。
VqImag = imag(Vq); figure surf(Xq,Yq,VqImag); xlabel('X'); ylabel('Y'); zlabel('Imaginary Value - V'); title('Imaginary Component of Interpolated Value');

分散データの内挿における問題への対応
前の節での多くの図解例は、滑らかな曲面でサンプリングした点集合の内挿に対応します。さらに、各点は比較的等間隔に配置されていました。たとえば、点のクラスターは、比較的大きな距離で区切られていませんでした。さらに、内挿は点の位置の凸包内で、評価されていました。
実際の内挿問題を扱う場合、データはもっと難しいものになるかもしれません。測定器によっては、不正確な読み取りがなされたり、または外れ値を生成する可能性があります。基となるデータは滑らかに変化せず、その値は、突然、点から点にジャンプすることがあります。この節では、散布データ内挿に伴う問題を特定し、対処するためのガイドラインを提供します。
NaN を含む入力データ
NaN 値を含むサンプル データを前処理して、このデータが内挿に貢献することができない場合、この NaN 値を削除しなければなりません。NaN が削除される場合、対応するデータの値/座標も削除され、整合性を確保しなければなりません。NaN 値が、サンプル データに存在する場合、コンストラクターが呼び出され、エラーを発生します。
以下の例は、NaN を削除する方法を説明します。
データを作成し、入力で NaN を置き換えます。
x = rand(25,1)*4-2; y = rand(25,1)*4-2; V = x.^2 + y.^2; x(5) = NaN; x(10) = NaN; y(12) = NaN; V(14) = NaN;
F = scatteredInterpolant(x,y,V);
NaN のサンプル点のインデックスを探索し、内挿を次のように作成します。nan_flags = isnan(x) | isnan(y) | isnan(V); x(nan_flags) = []; y(nan_flags) = []; V(nan_flags) = []; F = scatteredInterpolant(x,y,V);
NaN で置き換えます。X = rand(25,2)*4-2; V = X(:,1).^2 + X(:,2).^2; X(5,1) = NaN; X(10,1) = NaN; X(12,2) = NaN; V(14) = NaN;
F = scatteredInterpolant(X,V);
nan_flags = isnan(X(:,1)) | isnan(X(:,2)) | isnan(V); X(nan_flags,:) = []; V(nan_flags) = []; F = scatteredInterpolant(X,V);
内挿出力の NaN 値
'linear' メソッドまたは 'natural' メソッドを使用して凸包の外にある点をクエリすると、griddata と griddatan は NaN 値を返します。ただし、'nearest' メソッドを使用して同じ点をクエリすると、数値結果が得られます。これは、クエリ点の最近傍が凸包の内側と外側の両方に存在するためです。
凸包の外側で近似値を計算する場合は、scatteredInterpolant を使用してください。詳細は、散布データの外挿を参照してください。
重複する点の位置の取り扱い
入力データが「完全」であることは滅多になく、アプリケーションで重複するデータ点の位置を取り扱う必要がある場合があります。データ セットの中で同じ位置に存在する 2 つ以上のデータ点が別々の対応する値をもつことがあります。この場合、scatteredInterpolant は重複した点をマージし、対応する値の平均を計算します。次の例は、scatteredInterpolant が重複する点をもつデータ セットで内挿を実行する方法を示しています。
平面にあるいくつかのサンプル データを作成します。
x = rand(100,1)*6-3; y = rand(100,1)*6-3; V = x + y;
点 50 から点 100 の座標を代入して、重複する点の位置を導入します。
x(50) = x(100); y(50) = y(100);
内挿を作成します。
Fは 99 の一意のデータ点を含むことに注意してください。F = scatteredInterpolant(x,y,V)
50 番目の点に関連付けられた値を確認します。
F.Values(50)
もともと 50 番目と 100 番目のデータ点は同じ場所に位置するので、この 2 つのデータ点の値は、この 2 つの値の平均になります。
(V(50)+V(100))/2
一部の内挿の問題では、複数のサンプル値セットが同じ位置に対応している場合があります。たとえば、値セットが異なる周期で同じ位置に記録される場合があります。効率化のために、1 セットの読み込みを内挿して、次のセットを内挿するために値を置換することができます。
重複する点の位置で値を置換する場合、必ず一貫性のあるデータ管理を使用してください。100 のデータ点の位置に関連した 2 セットの値があり、値を置換して各セットを順に内挿するものとします。
次の 2 セットの値を検討します。
V1 = x + 4*y; V2 = 3*x + 5*y
内挿を作成します。
scatteredInterpolantは重複する位置をマージし、内挿には 99 個の固有なサンプル点があります。値をF = scatteredInterpolant(x,y,V1)
F.Values = V2で直接置換することは、100 の値を 99 のサンプルに代入することを意味します。前の結合操作のコンテキストは失われ、サンプル位置の数がサンプル値の数と一致しません。内挿は、クエリをサポートするために、不整合を解決する必要があります。
このようなさらに複雑な場合は、内挿を作成して編集する前に、重複を削除する必要があります。関数 unique を使用して、一意の点のインデックスを求めます。unique は重複する点のインデックスを識別する引数も出力できます。
[~, I, ~] = unique([x y],'first','rows'); I = sort(I); x = x(I); y = y(I); V1 = V1(I); V2 = V2(I); F = scatteredInterpolant(x,y,V1)
F を使用して、最初のデータ セットを内挿します。次に、値を置換して、2 番目のデータ セットを内挿することができます。F.Values = V2;
scatteredInterpolant の効率的な編集
scatteredInterpolant では、サンプル値 (F.Values) と内挿法 (F.Method) を表すプロパティを編集することができます。これらのプロパティは、基となる三角形分割から独立しているので、編集を効率的に実行できます。ただし、大規模な配列を操作する場合と同様、データを編集するときに不必要なコピーを作成しないように注意してください。コピーは、複数の変数が 1 つの配列を参照し、この配列が編集された場合に作成されます。
次の場合は、コピーは作成されません。
A1 = magic(4) A1(4,4) = 11
A1 と A2 は同じデータを共有できません。A1 = magic(4) A2 = A1 A1(4,4) = 32
scatteredInterpolant にはデータが含まれ、配列のように機能します。MATLAB 言語では、これは値オブジェクトと呼ばれます。MATLAB 言語は、アプリケーションがファイルに記述されている関数に構造化されている場合に最適なパフォーマンスを提供するように設計されています。コマンド ラインでのプロトタイプ化では、同じレベルのパフォーマンスが生まれない場合があります。次の例はこの動作を示していますが、この例のパフォーマンス ゲインはMATLAB内の他の関数に一般化されません。
このコードでは最適なパフォーマンスは生まれません。
x = rand(1000000,1)*4-2; y = rand(1000000,1)*4-2; z = x.*exp(-x.^2-y.^2); tic; F = scatteredInterpolant(x,y,z); toc tic; F.Values = 2*z; toc
MATLAB がファイル内に記述されている関数で構成されるプログラムを実行する場合、コードの実行の全体像を把握します。これにより MATLAB がパフォーマンスを最適化できます。コマンド ラインでコードを入力するときに、MATLAB は次に入力される内容を予測できないため、同じレベルの最適化を実行できません。再利用可能な関数を作成して、アプリケーションを開発することは一般的で推奨される方法であり、MATLAB はこの設定でパフォーマンスを最適化します。
内挿の結果が凸包の近傍で不適切
Delaunay 三角形分割は、良質な結果作成に適した幾何学的特性をもつことから、散布データの内挿問題に非常に適しています。以下のような特性があります。
等辺型の三角形や四面体を選択するための細長い三角形や四面体の棄却
2 点間の最近傍の関係を暗黙的に定義する空の外接円の性質
空の外接円の性質により、内挿値がクエリ位置の近傍内のサンプル点に影響されます。こうした性質にもかかわらず、状況によっては、データ点の分布が不適切な結果につながる可能性があります。一般的に、この現象はサンプル データ セットの凸包の近くで発生します。内挿が予期しない結果を生む場合、サンプル データのプロットおよび基本的な三角形分割により、問題の原因を調べることができます。
この例では、内挿された表面が境界の近くで悪化していることを示します。
境界の近傍の問題を表示するサンプル データ セットを作成します。
t = 0.4*pi:0.02:0.6*pi; x1 = cos(t)'; y1 = sin(t)'-1.02; x2 = x1; y2 = y1*(-1); x3 = linspace(-0.3,0.3,16)'; y3 = zeros(16,1); x = [x1;x2;x3]; y = [y1;y2;y3];
ここで、これらのサンプル点を表面 上に配置し、この表面の内挿を行います。
z = x.^2 + y.^2; F = scatteredInterpolant(x,y,z); [xi,yi] = meshgrid(-0.3:.02:0.3, -0.0688:0.01:0.0688); zi = F(xi,yi); mesh(xi,yi,zi) xlabel('X','fontweight','b'), ylabel('Y','fontweight','b') zlabel('Value - V','fontweight','b') title('Interpolated Surface');

実際の表面は次のとおりです。
zi = xi.^2 + yi.^2;
figure
mesh(xi,yi,zi)
title('Actual Surface')
内挿された面が境界の近傍で悪化する理由を把握するために、基本的な三角形分割を参照することは役立ちます。
dt = delaunayTriangulation(x,y); figure plot(x,y,'*r') axis equal hold on triplot(dt) plot(x1,y1,'-r') plot(x2,y2,'-r') title('Triangulation Used to Create the Interpolant') hold off
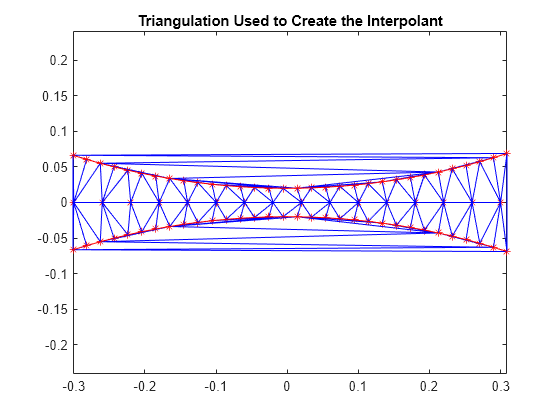
赤い境界線内の三角形は、比較的良い形状です。それは、近接する点から作られ、この領域で内挿がうまくいくからです。赤い境界線の外側で三角形は 細長い小片のようであり、互いに遠い点を接続します。正確に面をキャプチャするための十分なサンプルがないので、これらの領域における結果の質が悪くなることは当然のことです。3 次元では、三角形分割の視覚的な判断は少し複雑になりますが、点の分布を調べることで、可能な問題を表示することができます。
MATLAB® 4 griddata メソッド 'v4' は三角形分割に基づいていないため、境界近傍の内挿面の悪化による影響を受けません。
[xi,yi] = meshgrid(-0.3:.02:0.3, -0.0688:0.01:0.0688); zi = griddata(x,y,z,xi,yi,'v4'); mesh(xi,yi,zi) xlabel('X','fontweight','b'), ylabel('Y','fontweight','b') zlabel('Value - V','fontweight','b') title('Interpolated surface from griddata with v4 method','fontweight','b');

'v4' メソッドを使用すると、griddata から内挿された面は、想定される実際の面と一致します。