griddata
2 次元または 3 次元の散布データの内挿
構文
説明
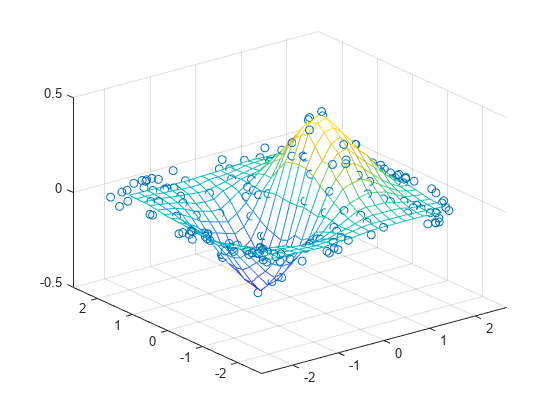
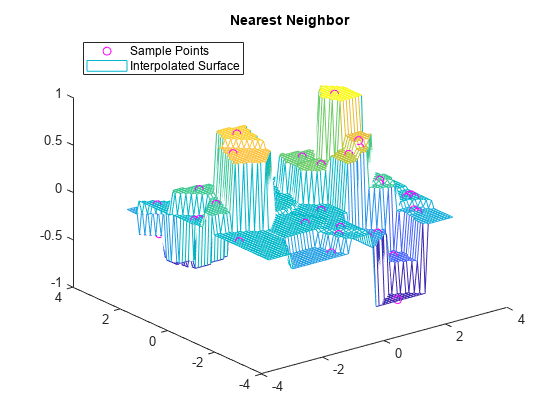
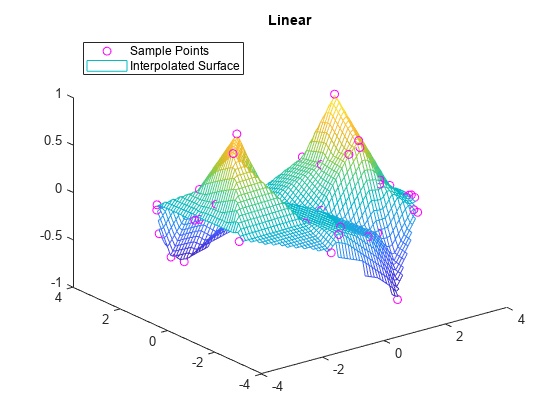
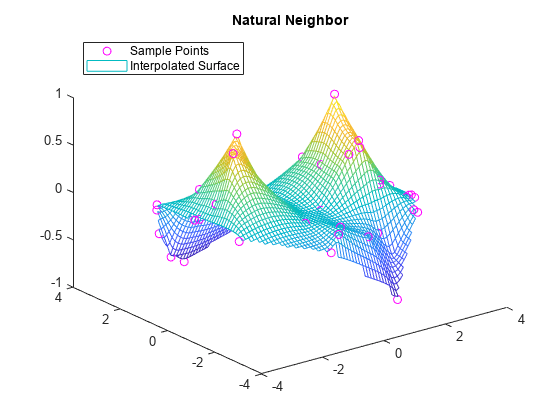
例
入力引数
出力引数
ヒント
griddataによる散布データの内挿ではデータの Delaunay 三角形分割を使用するため、x、yおよびzのスケーリング問題の影響を受けやすいことがあります。これが起きる場合は、normalizeを使用してデータを再スケーリングし、結果を改善することができます。詳細については、大きさが異なるデータの正規化を参照してください。
拡張機能
バージョン履歴
R2006a より前に導入