interpn

ndgrid 形式の 1 次元、2 次元、3 次元、N 次元グリッド データの内挿

構文

Vq = interpn(X1,X2,...,Xn,V,Xq1,Xq2,...,Xqn)

Vq = interpn(V,Xq1,Xq2,...,Xqn)

Vq = interpn(V)

Vq = interpn(V,k)

Vq = interpn(___,method)

Vq = interpn(___,method,extrapval)

説明

Vq = interpn(X1,X2,...,Xn,V,Xq1,Xq2,...,Xqn) は、線形内挿を使用して、特定のクエリ点における n 個の変数の関数の内挿値を返します。その結果は、関数の元のサンプリングを通過します。X1,X2,...,Xn には、サンプル点の座標が含まれます。V には、各サンプル点の対応する関数値が含まれます。Xq1,Xq2,...,Xqn には、クエリ点の座標が含まれます。

Vq = interpn(V,Xq1,Xq2,...,Xqn) は、サンプル点の既定のグリッドを想定します。既定のグリッドは、各次元の点 (1、2、3、...n) で構成されます。n_i の値は、V における次元の長さです。この構文は、点の間の絶対距離を考慮せず、メモリを節約する場合に使用します。

Vq = interpn(V) は、各次元で 1 回ずつサンプル値の間の区間を分割して形成される調整後のグリッドに、内挿値を返します。

Vq = interpn(V,k) は、各次元で区間の 2 分割を k 回繰り返して形成される調整後のグリッドに、内挿値を返します。この操作により、サンプル値の間に、2^k-1 個の内挿点が形成されます。

Vq = interpn(___,method) は代替内挿法として、'linear'、'nearest'、'pchip'、'cubic'、'makima' または 'spline' を指定します。既定の手法は、'linear' です。

Vq = interpn(___,method,extrapval) は、サンプル点の領域の外側に位置するすべてのクエリに割り当てられたスカラー値 extrapval も指定します。

サンプル点の領域の外側でクエリの extrapval 引数を省略すると、method 引数に基づき、interpn は次のいずれかを返します。

• 'spline' および 'makima' メソッドの場合、外挿値

• その他の内挿法の場合、NaN 値

例

1 次元内挿

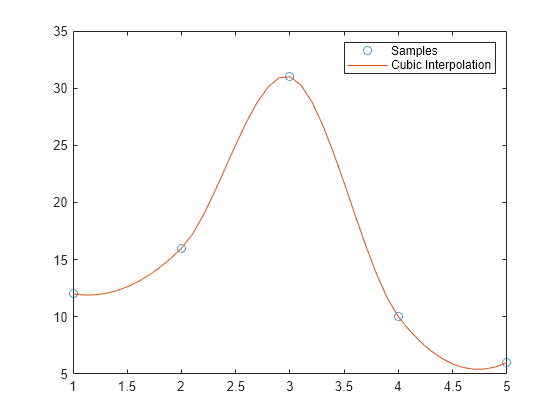
サンプル点と値を定義します。

x = [1 2 3 4 5];
v = [12 16 31 10 6];

クエリ点 xq を定義し、内挿を実行します。

xq = (1:0.1:5);
vq = interpn(x,v,xq,'cubic');

結果をプロットします。

figure
plot(x,v,'o',xq,vq,'-');
legend('Samples','Cubic Interpolation');

2 次元内挿

グリッド点のセットと対応するサンプル値を作成します。

[X1,X2] = ndgrid((-5:1:5));
R = sqrt(X1.^2 + X2.^2)+ eps;
V = sin(R)./(R);

ntimes=1 を使用して、より細かいグリッドに内挿します。

Vq = interpn(V,'cubic');
mesh(Vq);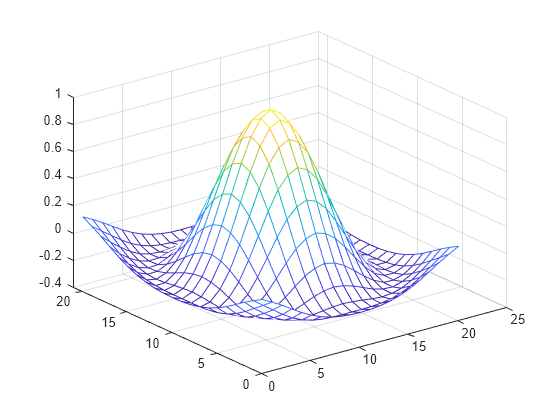

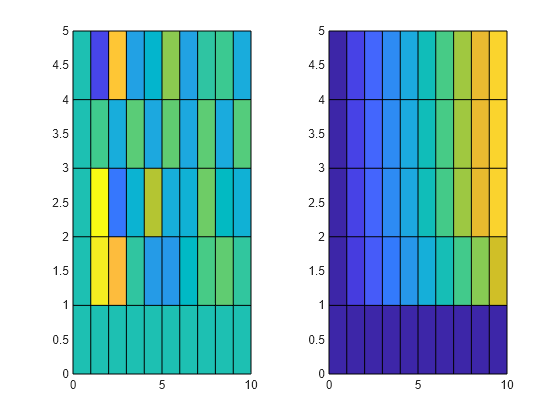
2 つの 2 次元サンプル値セットの内挿

ndgrid を使用して 2 次元サンプル点のグリッドを作成します。

[x,y] = ndgrid(0:10,0:5);

サンプル点における 2 つの異なるサンプル値セットを作成し、3 次元配列のページとして連結します。サンプル点に対して 2 つのサンプル値セットをプロットします。surf はグリッドに meshgrid 形式を使用しているので、プロットするために入力を転置します。

v1 = sin(x.*y)./(x+1);
v2 = x.*erf(y);
V = cat(3,v1,v2);
tiledlayout(1,2)
nexttile
surf(x',y',V(:,:,1)')
view(2)
nexttile
surf(x',y',V(:,:,2)')
view(2)

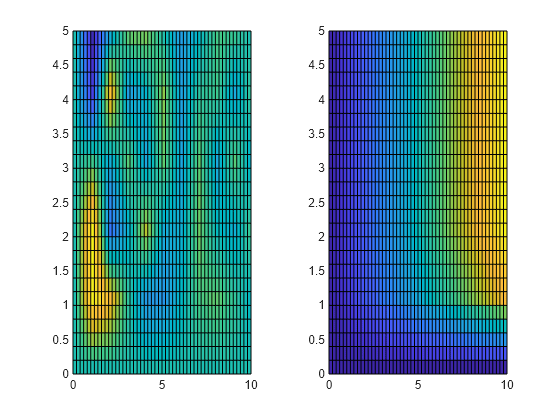
ndgrid を使用して内挿用のクエリ点のセットを作成してから、interpn を使用してクエリ点における各関数の値を求めます。内挿値をクエリ点に対してプロットします。

[xq,yq] = ndgrid(0:0.2:10);
Vq = interpn(x,y,V,xq,yq);
tiledlayout(1,2)
nexttile
surf(xq',yq',Vq(:,:,1)')
view(2)
nexttile
surf(xq',yq',Vq(:,:,2)')
view(2)

3 次元関数の領域の外側での評価

グリッド ベクトル x1、x2 および x3 を作成します。これらのベクトルは、V 内の値に関連付けられた点を定義します。

x1 = 1:100;
x2 = 1:50;
x3 = 1:30;

100×50×30 の乱数配列 V となるようにサンプル値を定義します。

rng default
V = rand(100,50,30);

x1、x2 および x3 の領域の外側にある 3 つの点で V を評価します。extrapval = -1 を指定します。

xq1 = [0 0 0];
xq2 = [0 0 51];
xq3 = [0 101 102];
vq = interpn(x1,x2,x3,V,xq1,xq2,xq3,'linear',-1)

vq = 1×3

    -1    -1    -1

3 つの点はすべて、x1、x2 および x3 の領域の外側にあるため、-1 と評価されます。

4 次元内挿

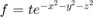を表す無名関数を定義します。

f = @(x,y,z,t) t.*exp(-x.^2 - y.^2 - z.^2);

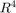で点のグリッドを作成します。次に、この関数を介して点を渡し、サンプル値 V を作成します。

[x,y,z,t] = ndgrid(-1:0.2:1,-1:0.2:1,-1:0.2:1,0:2:10);
V = f(x,y,z,t);

ここでクエリ グリッドを作成します。

[xq,yq,zq,tq] = ...
ndgrid(-1:0.05:1,-1:0.08:1,-1:0.05:1,0:0.5:10);

クエリ点で V を内挿します。

Vq = interpn(x,y,z,t,V,xq,yq,zq,tq);

ムービーを作成して、結果を表示します。

figure;
nframes = size(tq, 4);
for j = 1:nframes
   slice(yq(:,:,:,j),xq(:,:,:,j),zq(:,:,:,j),...
         Vq(:,:,:,j),0,0,0);
   clim([0 10]);
   M(j) = getframe;
end
movie(M);

入力引数

X1,X2,...,Xn — サンプル グリッド点

配列 | ベクトル

サンプル グリッド点。実数配列またはベクトルとして指定します。サンプル グリッド点は一意でなければなりません。

• X1,X2,...,Xn が配列の場合、(ndgrid 形式の) フル グリッドの座標が含まれます。X1,X2,...,Xn の配列を一緒に作成するには、関数 ndgrid を使用します。これらの配列は同じサイズでなければなりません。

• X1,X2,...,Xn がベクトルの場合、これらは グリッド ベクトルとして扱われます。これらのベクトルの値は厳密に単調で、増加または減少しなければなりません。

例: [X1,X2,X3,X4] = ndgrid(1:30,-10:10,1:5,10:13)

データ型: single | double

V — サンプル値

配列

サンプル値。実数配列または複素数配列として指定します。V のサイズ要件は、X1,X2,...,Xn で定義されるサンプル点のグリッドのサイズによって異なります。サンプル点 X1,X2,...,Xn は配列またはグリッド ベクトルにすることができますが、いずれの場合でも n 次元のグリッドを定義します。V は少なくとも同じ n 次元のサイズをもつ配列でなければなりませんが、n を超える余分な次元をもつこともできます。

• V も n 次元をもつ場合、V のサイズは X1,X2,...,Xn で定義される n 次元のグリッドのサイズと一致しなければなりません。この場合、V にはサンプル点における 1 つのサンプル値セットが含まれます。たとえば、X1,X2,X3 が 3×3×3 の配列の場合、V も 3×3×3 の配列にすることができます。

• V が n を超える次元をもつ場合、V の最初の n 次元のサイズは X1,X2,...,Xn で定義される n 次元のグリッドのサイズと一致しなければなりません。V の余分な次元は、サンプル点における余分なサンプル値のセットを定義します。たとえば、X1,X2,X3 が 3×3×3 の配列の場合、V を 3×3×3×2 の配列とすることができ、サンプル点における 2 つのサンプル値のセットを定義できます。

V に複素数が含まれる場合、interpn は実数部と虚数部を個別に内挿します。

例: rand(10,5,3,2)

データ型: single | double
複素数のサポート: あり

Xq1,Xq2,...,Xqn — クエリ点

スカラー | ベクトル | 配列

クエリ点。実数のスカラー、ベクトルまたは配列として指定します。

• Xq1,Xq2,...,Xqn がスカラーの場合、Rⁿ における単一のクエリ点の座標になります。

• Xq1,Xq2,...,Xqn がそれぞれの向きが異なるベクトルである場合、Xq1,Xq2,...,Xqn は、Rⁿ におけるグリッド ベクトルとして扱われます。

• Xq1,Xq2,...,Xqn が同じサイズと向きをもつベクトルの場合、Xq1,Xq2,...,Xqn は、Rⁿ における散布点として扱われます。

• Xq1,Xq2,...,Xqn が同じサイズの配列の場合、Rⁿ における、クエリ点 (ndgrid 形式) または散布点のフル グリッドを表します。

例: [X1,X2,X3,X4] = ndgrid(1:10,1:5,7:9,10:11)

データ型: single | double

k — 調整係数

1 (既定値) | 実数の非負の整数スカラー

調整係数。実数の非負のスカラー整数として指定します。この値は、各次元で調整されるグリッドの区間を分割する繰り返し回数を指定します。この操作により、サンプル値の間に、2^k-1 個の内挿点が形成されます。

k が 0 の場合、Vq は V と同じになります。

interpn(V,1) は、interpn(V) と同じです。

次の図は、R² における k=2 を示しています。赤色の内挿値が 72、黒のサンプル値が 9 つあります。

例: interpn(V,2)

データ型: single | double

method — 内挿法

'linear' (既定値) | 'nearest' | 'pchip' | 'cubic' | 'spline' | 'makima'

内挿法。次の表のオプションのいずれかとして指定します。

メソッド	説明	連続性	コメント
'linear'	クエリ点に内挿される値は、対応する各次元における、隣接するグリッド点の値を使用した線形内挿に基づいて決定されます。これは既定の内挿法です。	C0	各次元に少なくとも 2 つのグリッド点が必要 'nearest' よりも多いメモリが必要
'nearest'	クエリ点に内挿される値は、最も近いサンプル グリッド点の値になります。	不連続	各次元に 2 つのグリッド点が必要 中程度のメモリ要求で最高速の計算
'pchip'	形状維持区分的 3 次内挿 (1 次元のみ)。クエリ点に内挿される値は、隣接するグリッド点の値を使用した形状維持区分的 3 次内挿に基づいて決定されます。	C1	少なくとも 4 つの点が必要 'linear' よりも多くのメモリと長い計算時間が必要
'cubic'	クエリ点に内挿される値は、個々の次元で隣接するグリッド点の値の 3 次内挿に基づいて決定されます。内挿は、3 次畳み込みに基づいて決定されます。	C1	各次元でグリッドが等間隔でなければならない。ただし、すべての次元で間隔が同じである必要はありません。 各次元に少なくとも 4 つの点が必要 'linear' よりも多くのメモリと長い計算時間が必要
'makima'	修正 Akima 3 次エルミート内挿。クエリ点に内挿される値は、対応する各次元における隣接するグリッド点の値を使用した、最大 3 次の多項式の区分的関数に基づいて決定されます。Akima 式はオーバーシュートを回避するよう修正されています。	C1	各次元に少なくとも 2 つの点が必要 'spline' より少ない波形を生成 計算時間は通常 'spline' より短いが、メモリの要件は同様
'spline'	クエリ点に内挿される値は、個々の次元で隣接するグリッド点の値の 3 次内挿に基づいて決定されます。内挿は節点なし端点条件を使用した 3 次スプラインに基づいています。	C2	各次元に 4 つの点が必要 'cubic' よりも多くのメモリと長い計算時間が必要

extrapval — X1,X2,...,Xn の領域の外側の関数値

スカラー

X1,X2,...,Xn の領域の外側の関数値。実数または複素数のスカラーとして指定します。interpn は、X1,X2,...,Xn の領域の外側のすべての点に対して、この定数値を返します。

例: 5

例: 5+1i

データ型: single | double
複素数のサポート: あり

出力引数

Vq — 内挿値

スカラー | ベクトル | 配列

内挿値。実数または複素数のスカラー、ベクトルまたは配列として返されます。Vq のサイズと形状は、使用する構文、場合によっては入力引数のサイズと値によって異なることがあります。

• X1,X2,...,Xn でサンプル点を指定するか、既定のグリッドを使用していて、V がサンプル点の n 次元のグリッドと同じ次元数である場合、Vq には Xq1,Xq2,...,Xqn で定義されたクエリ点における単一の内挿値セットが含まれます。

  • Xq1,Xq2,...,Xqn がスカラーの場合、Vq はスカラーです。

  • Xq1,Xq2,...,Xqn が同じサイズと向きのベクトルの場合、Vq は同じサイズと向きのベクトルです。

  • Xq1,Xq2,...,Xqn が向きが混在するグリッドベクトルである場合、Vq はグリッド ベクトルによって暗黙的に定義されたグリッドと同じサイズの配列です。

  • Xq1,Xq2,...,Xqn が同じサイズの配列の場合、Vq は同じサイズの配列です。

• X1,X2,...,Xn でサンプル点を指定するか、既定のグリッドを使用していて、V の次元数がサンプル点の n 次元グリッドよりも多い場合、Vq には Xq1,Xq2,...,Xqn で定義されたクエリ点における複数の内挿値のセットが含まれます。この場合、Vq の最初の n 次元は、上記の単一の内挿値のセットのサイズ規則に従いますが、Vq は同じサイズの V と同じ余分な次元ももちます。

• 構文 interpn(V) と interpn(V,k) では、内挿は既定のグリッドを k 回分割することによって実行されます (interpn(V) の場合 k=1)。この場合、Vq は V と同じ次元数の配列で、i 番目の次元のサイズは 2^k * (size(V,i)-1)+1 です。

詳細

厳密に単調

反転せずに、常に増加または減少する一連の値。たとえば、シーケンス a = [2 4 6 8] は厳密に単調で増加します。シーケンス b = [2 4 4 6 8] は、b(2) と b(3) の間の値に変化がないため、厳密に単調ではありません。シーケンス c = [2 4 6 8 6] には c(4) と c(5) の間に反転が含まれているため、単調ではありません。

(ndgrid 形式の) フル グリッド

interpn の場合、フル グリッドは、n 個の配列 X1,X2,...,Xn で構成されます。その要素は Rⁿ における点のグリッドを表しています。i 番目の配列 Xi には、厳密に単調で増加し、i 番目の次元に沿って急速に変化する値が含まれます。

関数 ndgrid を使用して、interpn に渡すことができるフル グリッドを作成します。たとえば、次のコードは 1 ≤ X1 ≤ 3、1≤ X2 ≤ 4 の領域に対する、R² 内のフル グリッドを作成します。

[X1,X2] = ndgrid(-1:3,(1:4))

X1 =

    -1    -1    -1    -1
     0     0     0     0
     1     1     1     1
     2     2     2     2
     3     3     3     3


X2 =

     1     2     3     4
     1     2     3     4
     1     2     3     4
     1     2     3     4
     1     2     3     4

グリッド ベクトル

interpn の場合、グリッド ベクトルは、Rⁿ におけるグリッド上の点を定義する、向きが混在する n 個のベクトルから構成されます。

たとえば次のコードは、1 ≤ x1 ≤ 3、4 ≤ x2 ≤ 5、かつ 6 ≤x3≤ 8 の領域に対する、R³ 内のグリッド ベクトルを作成します。

x1 = 1:3;
x2 = (4:5)';
x3 = 6:8;

散布点

interpn の場合、散布点は、Rⁿ に散在する点の集合を定義する n 個の配列またはベクトル (Xq1,Xq2,...,Xqn) から構成されます。i 番目の配列 Xi には、i 番目の次元の座標が含まれています。

たとえば次のコードは、R³ における (1, 19, 10)、(6, 40, 1)、(15, 33, 22) および (0, 61, 13) の点を指定します。

Xq1 = [1 6; 15 0];
Xq2 = [19 40; 33 61];
Xq3 = [10 1; 22 13];

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• 最適な結果を得るには、X1,X2,...,Xn をベクトルとして指定してください。これらのベクトルの値は、厳密に単調で増加しなければなりません。

• コード生成は、'makima' 内挿法をサポートしていません。

• 内挿法は定数の文字ベクトルでなければなりません。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意事項および制限事項:

• 最大で 5 次元がサポートされます。

• X1,X2,...,Xn は V と一致する次元をもたなければなりません。

• method は、'linear' または 'nearest' でなければなりません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意事項および制限事項:

• X1,X2,...,Xn は V と一致する次元をもたなければなりません。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

R2021a: 複数のデータ セットを同時に内挿

同じクエリ点における同じグリッド上で複数のデータ セットを内挿できるようになりました。たとえば、2 次元グリッド、グリッド点の値の 3 次元配列、およびクエリ点の 2 次元集合を指定すると、interpn は、値の 3 次元配列内の各 2 次元ページのクエリ点における内挿値を返します。

参考

interp1 | interp2 | interp3 | ndgrid