interp2

meshgrid 形式の 2 次元グリッド データの内挿

構文

Vq = interp2(X,Y,V,Xq,Yq)

Vq = interp2(V,Xq,Yq)

Vq = interp2(V)

Vq = interp2(V,k)

Vq = interp2(___,method)

Vq = interp2(___,method,extrapval)

説明

Vq = interp2(X,Y,V,Xq,Yq) は、線形内挿を使用して、特定のクエリ点における 2 変数をもつ関数の内挿値を返します。その結果は、関数の元のサンプリングを通過します。X と Y には、サンプル点の座標が含まれます。V には、各サンプル点の対応する関数値が含まれます。Xq と Yq には、クエリ点の座標が含まれます。

Vq = interp2(V,Xq,Yq) は、サンプル点の既定のグリッドを想定します。既定のグリッド点は、四角形領域 X=1:n、Y=1:m をカバーします。ここで [m,n] = size(V) です。この構文は、点の間の絶対距離を考慮せず、メモリを節約する場合に使用します。

Vq = interp2(V) は、各次元で 1 回ずつサンプル値の間の区間を分割して形成される調整後のグリッドに、内挿値を返します。

Vq = interp2(V,k) は、各次元で区間の 2 分割を k 回繰り返して形成される調整後のグリッドに、内挿値を返します。この操作により、サンプル値の間に、2^k-1 個の内挿点が形成されます。

Vq = interp2(___,method) は代替内挿法として、'linear'、'nearest'、'cubic'、'makima' または 'spline' を指定します。既定の手法は、'linear' です。

Vq = interp2(___,method,extrapval) は、サンプル点の領域の外側に位置するすべてのクエリに割り当てられたスカラー値 extrapval も指定します。

サンプル点の領域の外側でクエリの extrapval 引数を省略すると、method 引数に基づき、interp2 は次のいずれかを返します。

• 'spline' および 'makima' メソッドの場合、外挿値

• その他の内挿法の場合、NaN 値

例

既定の方法によるグリッドへの内挿

関数 peaks を粗くサンプリングします。

[X,Y] = meshgrid(-3:3);
V = peaks(X,Y);

粗いサンプリングをプロットします。

figure
surf(X,Y,V)
title('Original Sampling');

0.25 の間隔でクエリ グリッドを作成します。

[Xq,Yq] = meshgrid(-3:0.25:3);

クエリ点で内挿します。

Vq = interp2(X,Y,V,Xq,Yq);

結果をプロットします。

figure
surf(Xq,Yq,Vq);
title('Linear Interpolation Using Finer Grid');

3 次法によるグリッドへの内挿

関数 peaks を粗くサンプリングします。

[X,Y] = meshgrid(-3:3);
V = peaks(7);

粗いサンプリングをプロットします。

figure
surf(X,Y,V)
title('Original Sampling');

0.25 の間隔でクエリ グリッドを作成します。

[Xq,Yq] = meshgrid(-3:0.25:3);

クエリ点で内挿し、3 次内挿を指定します。

Vq = interp2(X,Y,V,Xq,Yq,'cubic');

結果をプロットします。

figure
surf(Xq,Yq,Vq);
title('Cubic Interpolation Over Finer Grid');

グレースケール イメージの調整

イメージ データをワークスペースに読み込みます。

load flujet.mat
colormap gray

イメージの小さい領域を取り出して、単精度にキャストします。

V = single(X(200:300,1:25));

イメージ領域を表示します。

imagesc(V);
axis off
title('Original Image')

各次元で調整されるグリッドの各点の間の区間を 5 回繰り返し分割し、内挿値を挿入します。

Vq = interp2(V,5);

結果を表示します。

imagesc(Vq);
axis off
title('Linear Interpolation')

X と Y の領域の外側での評価

両方の次元で、範囲 [-2, 2] で関数を粗くサンプリングします。

[X,Y] = meshgrid(-2:0.75:2);
R = sqrt(X.^2 + Y.^2)+ eps;
V = sin(R)./(R);

粗いサンプリングをプロットします。

figure
surf(X,Y,V)
xlim([-4 4])
ylim([-4 4])
title('Original Sampling')

X と Y の領域を越えるクエリ グリッドを作成します。

[Xq,Yq] = meshgrid(-3:0.2:3);

X と Y の領域内で 3 次内挿を実行し、範囲外に位置するすべてのクエリに 0 を割り当てます。

Vq = interp2(X,Y,V,Xq,Yq,'cubic',0);

結果をプロットします。

figure
surf(Xq,Yq,Vq)
title('Cubic Interpolation with Vq=0 Outside Domain of X and Y');

入力引数

X,Y — サンプル グリッド点

行列 | ベクトル

サンプル グリッド点。実数行列またはベクトルとして指定します。サンプル グリッド点は一意でなければなりません。

• X と Y が行例の場合、(meshgrid 形式の) フル グリッドの座標が含まれています。X 行列と Y 行列を一緒に作成するには、関数 meshgrid を使用します。両方の行列が同じサイズでなければなりません。

• X および Y がベクトルの場合、グリッド ベクトルとして扱われます。両方のベクトルの値は厳密に単調で、増加または減少しなければなりません。

例: [X,Y] = meshgrid(1:30,-10:10)

データ型: single | double

V — サンプル値

行列

サンプル値。実数行列または複素数行列として指定します。V のサイズ要件は、X と Y のサイズによって異なります。

• X と Y が (meshgrid 形式の) フル グリッドを表す行列の場合、V は X および Y と同じサイズでなければなりません。

• X と Y がグリッド ベクトルの場合、V は、length(Y) 行と length(X) 列を含む行列でなければなりません。

V に複素数が含まれる場合、interp2 は実数部と虚数部を個別に内挿します。

例: rand(10,10)

データ型: single | double
複素数のサポート: あり

Xq,Yq — クエリ点

スカラー | ベクトル | 行列 | 配列

クエリ点。実数のスカラー、ベクトル、行列または配列として指定します。

• Xq と Yq がスカラーの場合、単一のクエリ点の座標になります。

• Xq と Yq が異なる向きのベクトルの場合、Xq と Yq はグリッド ベクトルとして扱われます。

• Xq と Yq が、サイズと向きが同じベクトルの場合、Xq と Yq は 2 次元空間の散布点として扱われます。

• Xq と Yq が行列の場合、これらはクエリ点 (meshgrid 形式) または散布点のフル グリッドを表します。

• Xq と Yq が N 次元配列の場合、2 次元空間内の散布点を表します。

例: [Xq,Yq] = meshgrid((1:0.1:10),(-5:0.1:0))

データ型: single | double

k — 調整係数

1 (既定値) | 実数の非負の整数スカラー

調整係数。実数の非負のスカラー整数として指定します。この値は、各次元で調整されるグリッドの区間を分割する繰り返し回数を指定します。この操作により、サンプル値の間に、2^k-1 個の内挿点が形成されます。

k が 0 の場合、Vq は V と同じになります。

interp2(V,1) は、interp2(V) と同じです。

次の図は、k=2 の 9 つのサンプル値 (黒) 間での内挿値 (赤) の配置を示しています。

例: interp2(V,2)

データ型: single | double

method — 内挿法

'linear' (既定値) | 'nearest' | 'cubic' | 'spline' | 'makima'

内挿法。次の表のオプションのいずれかとして指定します。

メソッド	説明	連続性	コメント
'linear'	クエリ点に内挿される値は、対応する各次元における、隣接するグリッド点の値を使用した線形内挿に基づいて決定されます。これは既定の内挿法です。	C0	各次元に少なくとも 2 つのグリッド点が必要 'nearest' よりも多いメモリが必要
'nearest'	クエリ点に内挿される値は、最も近いサンプル グリッド点の値になります。	不連続	各次元に 2 つのグリッド点が必要 中程度のメモリ要求で最高速の計算
'cubic'	クエリ点に内挿される値は、個々の次元で隣接するグリッド点の値の 3 次内挿に基づいて決定されます。内挿は、3 次畳み込みに基づいて決定されます。	C1	各次元でグリッドが等間隔でなければならない。ただし、すべての次元で間隔が同じである必要はありません。 各次元に少なくとも 4 つの点が必要 'linear' よりも多くのメモリと長い計算時間が必要
'makima'	修正 Akima 3 次エルミート内挿。クエリ点に内挿される値は、対応する各次元における隣接するグリッド点の値を使用した、最大 3 次の多項式の区分的関数に基づいて決定されます。Akima 式はオーバーシュートを回避するよう修正されています。	C1	各次元に少なくとも 2 つの点が必要 'spline' より少ない波形を生成 計算時間は通常 'spline' より短いが、メモリの要件は同様
'spline'	クエリ点に内挿される値は、個々の次元で隣接するグリッド点の値の 3 次内挿に基づいて決定されます。内挿は節点なし端点条件を使用した 3 次スプラインに基づいています。	C2	各次元に 4 つの点が必要 'cubic' よりも多くのメモリと長い計算時間が必要

extrapval — X と Y の領域の外側の関数値

スカラー

X と Y の領域の外側の関数値。実数または複素数のスカラーとして指定します。interp2 は、X と Y の領域の外側のすべての点に対して、この定数値を返します。

例: 5

例: 5+1i

データ型: single | double
複素数のサポート: あり

出力引数

Vq — 内挿値

スカラー | ベクトル | 行列

内挿値。実数または複素数のスカラー、ベクトルまたは行列として返されます。Vq のサイズと形状は、使用する構文、場合によっては入力引数のサイズと値によって異なることがあります。

構文	特殊な条件	Vq のサイズ	例
interp2(X,Y,V,Xq,Yq) interp2(V,Xq,Yq) と、method または extrapval を含む上記構文のバリエーション	Xq、Yq はスカラー	スカラー	Xq と Yq をスカラーとして渡した場合は size(Vq) = [1 1]。
上記に同じ	Xq、Yq は、サイズと向きが同じベクトル	Xq および Yq と同じサイズと向きをもつベクトル	size(Xq) = [100 1] かつ size(Yq) = [100 1] の場合、 size(Vq) = [100 1]。
上記に同じ	Xq、Yq は、向きが混在するベクトル	行の数が length(Yq) で、列の数が length(Xq) の行列	size(Xq) = [1 100] かつ size(Yq) = [50 1] の場合、 size(Vq) = [50 100]。
上記に同じ	Xq、Yq は、同じサイズの行列または配列	Xq および Yq と同じサイズの行列または配列	size(Xq) = [50 25] かつ size(Yq) = [50 25] の場合、 size(Vq) = [50 25]。
interp2(V,k) と、method または extrapval を含む上記構文のバリエーション	なし	行の数が 2^k * (size(V,1)-1)+1、 列の数が 2^k * (size(V,2)-1)+1 の行列	size(V) = [10 20] かつ k = 2 の場合、 size(Vq) = [37 77]。

詳細

厳密に単調

反転せずに、常に増加または減少する一連の値。たとえば、シーケンス a = [2 4 6 8] は厳密に単調で増加します。シーケンス b = [2 4 4 6 8] は、b(2) と b(3) の間の値に変化がないため、厳密に単調ではありません。シーケンス c = [2 4 6 8 6] には c(4) と c(5) の間に反転が含まれているため、単調ではありません。

(meshgrid 形式の) フル グリッド

interp2 の場合、フル グリッドは、要素が四角形領域の点のグリッドを表す行列のペアです。1 つの行列には x 座標、もう 1 つの行列には y 座標が含まれます。x 行列の値は、厳密に単調で、行に沿って増加します。列に沿った値は定数です。y 行列の値は厳密に単調で、列に沿って増加します。行に沿った値は定数です。関数 meshgrid を使用して、interp2 に渡すことができるフル グリッドを作成します。

たとえば、次のコードは –1 ≤ x ≤ 3 かつ 1 ≤ y ≤ 4 の領域に対するフル グリッドを作成します。

[X,Y] = meshgrid(-1:3,(1:4))

X =

    -1     0     1     2     3
    -1     0     1     2     3
    -1     0     1     2     3
    -1     0     1     2     3

Y =

     1     1     1     1     1
     2     2     2     2     2
     3     3     3     3     3
     4     4     4     4     4

グリッド ベクトルは、フル グリッドよりもグリッドをコンパクトに表すことができる形式です。この 2 つの形式と、サンプル値の行列 V の関係は次のとおりです。

グリッド ベクトル

interp2 の場合、グリッド ベクトルは、グリッド内の x 座標と y 座標を定義するベクトルのペアから構成されます。行ベクトルは x 座標を定義し、列ベクトルは y 座標を定義します。

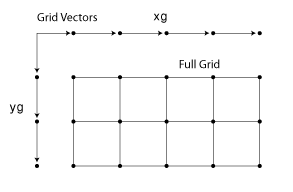
たとえば、次のコードは –1 ≤ x ≤ 3 かつ 1 ≤ y ≤ 4 の領域を指定するグリッド ベクトルを作成します。

x = -1:3;
y = (1:4)';

散布点

interp2 の場合、散布点は、2 次元空間に散在する点の集合を定義する配列のペアから構成されます。1 つの配列には x 座標、もう 1 つの配列には y 座標が含まれます。

たとえば、次のコードは (2,7)、(5,3)、(4,1) および (10,9) の点を指定します。

x = [2 5; 4 10];
y = [7 3; 1 9];

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• Xq と Yq は同じサイズでなければなりません。meshgrid を使用してグリッドで評価します。

• 最適な結果を得るには、X および Y をベクトルとして指定してください。これらのベクトルの値は、厳密に単調で増加しなければなりません。

• コード生成は、'makima' 内挿法をサポートしていません。

• 'cubic' 内挿法の場合、グリッドが等間隔でなければ結果はエラーとなります。この場合は、'spline' 内挿法を使用します。

• 最適な結果を得るには、'spline' 内挿法を使用するときに、以下を実行してください。

  • meshgrid を使用して、入力 Xq と Yq を作成します。

  • V の次元に相対的な少数の内挿点を使用します。大規模な一連の散布点に対して内挿すると、非効率的になる可能性があります。

GPU コード生成

GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

使用上の注意事項および制限事項:

• Xq と Yq は同じサイズでなければなりません。meshgrid を使用してグリッドで評価します。

• 最適な結果を得るには、X および Y をベクトルとして指定してください。これらのベクトルの値は、厳密に単調で増加しなければなりません。

• コード生成は、'makima' 内挿法をサポートしていません。

• 'cubic' 内挿法の場合、グリッドが等間隔でなければ結果はエラーとなります。この場合は、'spline' 内挿法を使用します。

• 最適な結果を得るには、'spline' 内挿法を使用するときに、以下を実行してください。

  • meshgrid を使用して、入力 Xq と Yq を作成します。

  • V の次元に相対的な少数の内挿点を使用します。大規模な一連の散布点に対して内挿すると、非効率的になる可能性があります。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意事項および制限事項:

• V は double または single の 2 次元配列でなければなりません。V は実数または複素数にできます。V をベクトルにすることはできません。

• X と Y は以下の条件を満たさなければなりません。

  • 型が同じである (double または single)。

  • 対応する次元において増加し重複がない要素をもつ有限ベクトルまたは 2 次元配列である。

  • X と Y が非ベクトルの 2 次元配列である場合に直交座標軸と一致する (meshgrid で生成された場合と同様)。

  • 次元が V と一致する。

• Xq と Yq は同じ型 (double または single) のベクトルまたは配列でなければなりません。Xq と Yq が配列の場合、それらのサイズは同じでなければなりません。長さが異なるベクトルである場合は、方向も異なっていなければなりません。

• method は、'linear'、'nearest' または 'cubic' でなければなりません。

• 境界外入力の外挿はサポートされていません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

この関数は分散配列を完全にサポートしています。詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

griddata | interp1 | interp3 | interpn | meshgrid | griddedInterpolant | scatteredInterpolant

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい