ndgrid

N 次元空間での四角形のグリッド

構文

[X1,X2,...,Xn] = ndgrid(x1,x2,...,xn)

[X1,X2,...,Xn] = ndgrid(xg)

説明

[X1,X2,...,Xn] = ndgrid(x1,x2,...,xn) は、グリッド ベクトル x1,x2,...,xn を複製して、n 次元のフル グリッドを生成します。

[X1,X2,...,Xn] = ndgrid(xg) は、すべての次元に対して使用する 1 つのグリッド ベクトル xg を指定します。指定する出力引数の数により、出力の次元 n が決定されます。

例

2 次元グリッドを作成

ベクトル [1 3 5 7 9 11 13 15 17 19] および [2 4 6 8 10 12] から 2 次元グリッドを作成します。

[X,Y] = ndgrid(1:2:19,2:2:12)

X = 10×6

     1     1     1     1     1     1
     3     3     3     3     3     3
     5     5     5     5     5     5
     7     7     7     7     7     7
     9     9     9     9     9     9
    11    11    11    11    11    11
    13    13    13    13    13    13
    15    15    15    15    15    15
    17    17    17    17    17    17
    19    19    19    19    19    19

Y = 10×6

     2     4     6     8    10    12
     2     4     6     8    10    12
     2     4     6     8    10    12
     2     4     6     8    10    12
     2     4     6     8    10    12
     2     4     6     8    10    12
     2     4     6     8    10    12
     2     4     6     8    10    12
     2     4     6     8    10    12
     2     4     6     8    10    12

内挿を使用したグリッドの調整

四角形のグリッドを作成し、そのグリッドで関数値を計算します。割り当てられた値の間に内挿して、グリッドを調整します。

$$(x,y)$$ の粗いグリッドを作成します。$$x$$ の範囲は $$[-6,6]$$、$$y$$ の範囲は $$[-3,3]$$ です。

[X,Y] = ndgrid(-6:0.5:6,-3:0.5:3);

グリッドで定義される位置で関数を評価します。その後、表面プロットを使用して関数を可視化します。あるいは、R2016b 以降では、このタスクに暗黙的な拡張を使用できます。

f = sin(X.^2) .* cos(Y.^2);
surf(Y,X,f)

より調整されたグリッド (Xq,Yq) で点の間を内挿します。その後、表面プロットを使用して内挿値を可視化します。

[Xq,Yq] = ndgrid(-6:0.125:6,-3:0.125:3);
F = interpn(X,Y,f,Xq,Yq,"spline");
surf(Yq,Xq,F)

入力引数

x1,x2,...,xn — グリッド ベクトル (個別の引数として指定)

ベクトル

グリッド ベクトル。各次元のグリッド座標を含むベクトルとして指定します。グリッド ベクトルは暗黙的にグリッドを定義します。たとえば、2 次元の場合は次のようになります。

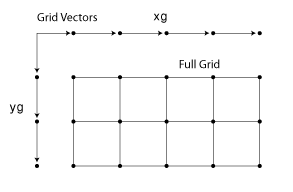
データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
複素数のサポート: あり

xg — すべての次元に使用するグリッド ベクトル

ベクトル

すべての次元に使用するグリッド ベクトル。グリッド座標を含むベクトルとして指定します。ndgrid は xg を各次元のグリッド ベクトルとして使用します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
複素数のサポート: あり

出力引数

X1,X2,...,Xn — フル グリッド表現

配列

フル グリッド表現。個別の配列として返されます。出力配列 Xi のそれぞれについて、i 番目の次元にグリッド ベクトル xi のコピーが含まれます。

詳細

meshgrid と ndgrid の形式の変換

meshgrid と ndgrid は異なる出力形式を使用してグリッドを作成します。具体的には、これらの関数の一方を使用して作成されたグリッドをもう一方のグリッド形式と比較すると、最初の 2 つの次元が入れ替わっています。MATLAB^® 関数には meshgrid の形式のグリッドを使用する関数も ndgrid の形式を使用する関数もあるため、2 つの形式の間でグリッドを変換することがよくあります。

これらのグリッド形式は、pagetranspose (R2020b 以降) または permute を使用してグリッド配列の最初の 2 つの次元を入れ替えることで変換できます。たとえば、meshgrid で 3 次元グリッドを作成します。

[X,Y,Z] = meshgrid(1:4,1:3,1:2);

次に、各グリッド配列の最初の 2 つの次元を転置してグリッドを ndgrid の形式に変換し、結果を ndgrid の出力と比較します。

Xt = pagetranspose(X);
Yt = pagetranspose(Y);
Zt = pagetranspose(Z);
[Xn,Yn,Zn] = ndgrid(1:4,1:3,1:2);
isequal(Xt,Xn) & isequal(Yt,Yn) & isequal(Zt,Zn)

ans =

  logical

   1

pagetranspose の使用は、他の次元はそのままで最初の 2 つの次元を並べ替えるのと同じです。この操作は permute(X,[2 1 3:ndims(X)]) を使用して実行することもできます。

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

ndgrid 関数は GPU 配列入力をサポートしますが、次の使用上の注意および制限があります。

• 1 次元構文 X = ndgrid(x) は、gpuArray の列ベクトル X を返します。この列ベクトルには、1 次元グリッドとして使用する入力 gpuArray x の要素が格納されます。

• 入力は浮動小数点の double または single でなければなりません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意および制限:

• 1 次元構文 X = ndgrid(x) は、分散配列の列ベクトル X を返します。この列ベクトルには、1 次元グリッドとして使用する入力分散配列 x の要素が格納されます。

• 入力は浮動小数点の double または single でなければなりません。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

griddedInterpolant | mesh | meshgrid | combinations | surf

トピック

• グリッド データの内挿