グリッド データの内挿

グリッド データは、グリッドを形成する等間隔の点の値または測定値で構成されます。気象学、測量、医用画像など、多くの分野でグリッド データが使用されます。それらの分野では、定期的な空間区間で、おそらくは経時的に測定値を取得するのが一般的です。1 次元 (単純な時系列) のものから 4 次元 (経時的な体積の測定) を超えるものまで、さまざまな範囲の整理されたデータのグリッドがあります。グリッド データの例をいくつか示します。

• 1 次元: 株価の経時的な変動

• 2 次元: 表面の温度

• 3 次元: 脳の MRI イメージ

• 4 次元: 海水の体積の経時的な測定

これらのいずれの用途でも、グリッドベースの内挿により、データの有用性が測定値のない点にも効率的に拡張されます。たとえば、株価の 1 時間ごとのデータがあれば、内挿を使用して 15 分ごとの価格を近似できます。

MATLAB のグリッド内挿関数

MATLAB^® には、グリッドベースの内挿用のツールがいくつか用意されています。

グリッド作成関数

関数 meshgrid および ndgrid は、さまざまな次元のグリッドを作成します。meshgrid では 2 次元または 3 次元のグリッドを作成でき、ndgrid では任意の次元数のグリッドを作成できます。これらの関数は異なる出力形式を使用してグリッドを返します。これらのグリッド形式は、関数 pagetranspose ("R2020b 以降") または permute を使用してグリッドの最初の 2 つの次元を入れ替えることで変換できます。

内挿関数

interp の関数群には、interp1、interp2、interp3、および interpn があります。各関数が特定の次元数でデータを内挿するように設計されています。interp2 と interp3 は meshgrid の形式のグリッドを使用し、interpn は ndgrid の形式のグリッドを使用します。

内挿オブジェクト

griddedInterpolant オブジェクトは、ndgrid の形式のデータに対する任意の次元数での内挿をサポートします。これらのオブジェクトは複数値の内挿もサポートし ("R2021a 以降")、各グリッド点に複数の値を関連付けることができます。

griddedInterpolant オブジェクトを使用すると、関数 interp よりもメモリとパフォーマンスに関して有利になります。関数 interp は呼び出されるたびに新しい計算を実行するのに対し、griddedInterpolant は内挿オブジェクトへのクエリが繰り返される場合のパフォーマンスが非常に効率的です。また、griddedInterpolant はメモリ効率が高い形式 (コンパクト グリッド) でサンプル点を格納し、マルチコア コンピューター プロセッサを利用したマルチスレッドに対応しています。

グリッド表現

MATLAB では、グリッドを 3 つの表現方法、フル グリッド、コンパクト グリッドおよび既定のグリッドのうちのいずれかで表現できます。既定のグリッドとコンパクト グリッドは、主として利便性と効率の向上を求める場合にそれぞれ使用されます。

フル グリッド

"フル グリッド" は、すべての点を明示的に定義するグリッドです。フル グリッドは ndgrid と meshgrid の出力により定義されます。フル グリッドでは、各次元の点の間隔が等しい "等間隔" のグリッドと、1 つ以上の次元で間隔が異なる "非等間隔" のグリッドを作成できます。等間隔グリッドには、それぞれの次元内で間隔が一定であれば、次元ごとの間隔が異なるものも含まれます。

等間隔	等間隔	非等間隔

等間隔のフル グリッドの例を次に示します。

[X,Y] = meshgrid([1 2 3],[3 6 9 12])

X =

     1     2     3
     1     2     3
     1     2     3
     1     2     3


Y =

     3     3     3
     6     6     6
     9     9     9
    12    12    12

コンパクト グリッド

大規模なグリッドを扱う場合、グリッドのすべての点を明示的に定義すると大量のメモリが使用される可能性があります。"コンパクト グリッド" 表現では、フル グリッドほどメモリのオーバーヘッドは必要とされません。コンパクト グリッド表現では、フル グリッドの代わりに "グリッド ベクトル" (次元ごとに 1 つ) のみが保存されます。それらのグリッド ベクトルの組み合わせから暗黙的にグリッドが定義されます。実際、meshgrid および ndgrid の入力はグリッド ベクトルであり、それらの関数ではグリッド ベクトルを複製してフル グリッドを形成します。コンパクト グリッド表現を使用すると、グリッドの作成を行わずに、グリッド ベクトルを内挿関数に直接指定できます。

たとえば、x1 = 1:3 と x2 = 1:5 の 2 つのベクトルを考えます。これらのベクトルは、次のような x1 方向の座標セットと x2 方向の座標セットと考えることができます。

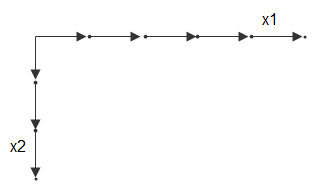
各矢印は位置を示しています。これら 2 つのベクトルを使用してグリッド点のセットを定義できます。この場合、x1 が 1 つの座標セットを、x2 がもう 1 つの座標セットを指定します。グリッド ベクトルを複製すると、2 つの座標配列が形成され、フル グリッドが構成されます。

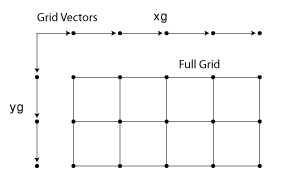
入力グリッド ベクトルは、"単調" または "非単調" にすることができます。単調ベクトルでは、ベクトル内の値はその次元において常に増加、または常に減少のいずれかになります。一方、非単調ベクトルでは、値は増減します。[2 4 6 3 1] などのように入力グリッド ベクトルが非単調の場合、[X1,X2] = ndgrid([2 4 6 3 1]) の出力は非単調グリッドになります。グリッドを他の MATLAB 関数に渡す場合は、グリッド ベクトルは単調でなければなりません。単調性を確保するには、関数 sort を使用すると便利です。

既定のグリッド

用途によっては、グリッド点の値のみが重要で、グリッド点の間の距離は重要でない場合があります。たとえば、ほとんどの MRI スキャンでは、すべての方向において等間隔のデータを収集します。このような場合、データで使用する "既定のグリッド" 表現を内挿関数で自動的に生成できます。これを行うには、内挿関数へのグリッド入力を省略します。グリッド入力を省略すると、関数で自動的に単位間隔のグリッドのデータであると見なされます。この単位間隔のグリッドが関数の実行時に作成され、グリッドを自分で作成する手間が省けます。

例: 2 次元グリッドでの温度の内挿

表面の温度を各方向に 5 cm 間隔で 20 cm まで等間隔に収集したデータがあるとします。meshgrid を使用してフル グリッドを作成します。

[X,Y] = meshgrid(0:5:20)

X =

     0     5    10    15    20
     0     5    10    15    20
     0     5    10    15    20
     0     5    10    15    20
     0     5    10    15    20


Y =

     0     0     0     0     0
     5     5     5     5     5
    10    10    10    10    10
    15    15    15    15    15
    20    20    20    20    20

各グリッド点の (x,y) 座標が X と Y の行列の対応する要素として表されます。最初のグリッド点は [X(1) Y(1)] で与えられる [0 0]、次のグリッド点は [X(2) Y(2)] で与えられる [0 5] のようになります。

次に、温度の測定値をグリッドで表す行列を作成し、データを表面としてプロットします。

T = [1   1   10   1   1; 
     1   10  10   10  10;  
     100 100 1000 100 100; 
     10  10  10   10  1;
     1   1   10   1   1];
surf(X,Y,T)
view(2)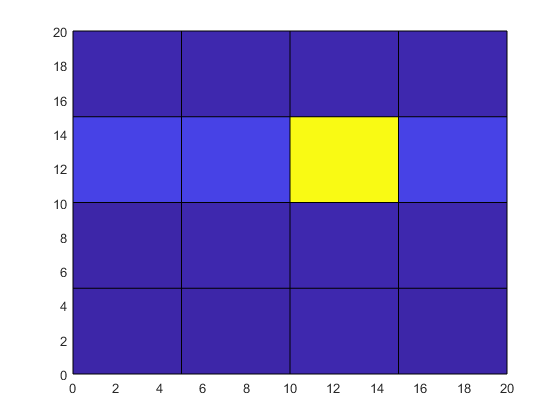

中央のグリッド点の温度が高くなっていますが、その位置と周囲のグリッド点への影響が生データからはわかりません。

データの分解能を 10 倍に上げるには、interp2 を使用して、0.5 cm 間隔のより細かいグリッドに温度データを内挿します。もう一度 meshgrid を使用して、行列 Xq と Yq で表現される細かいグリッドを作成します。その後、元のグリッド、温度データ、および新しいグリッド点で interp2 を使用して、結果のデータをプロットします。既定では、interp2 は各次元に線形内挿を使用します。

[Xq,Yq] = meshgrid(0:0.5:20);
Tq = interp2(X,Y,T,Xq,Yq);
surf(Xq,Yq,Tq)
view(2)

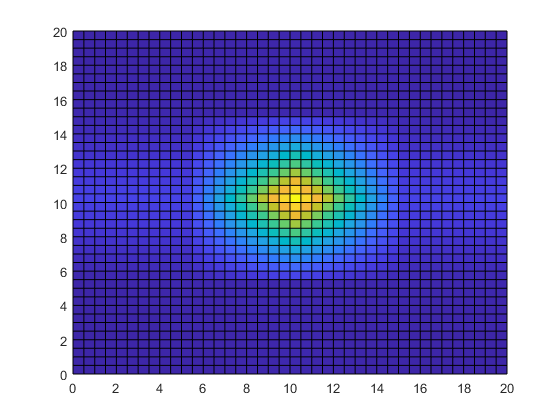
温度データを内挿すると、イメージが詳細になり、測定値の領域内におけるデータの有用性が大幅に向上します。

グリッド内挿法

MATLAB のグリッドベースの内挿の関数およびオブジェクトでは、いくつかの異なる方法の内挿が提供されます。内挿法の選択によっては、計算時間が長くなり、大量のメモリが必要になることに注意してください。必要な平滑度を得るには、長時間の計算と大量のメモリ使用を受け入れざるをえない場合があります。次の表に、同じ 1 次元に適用されるそれぞれの内挿法のプレビューと、それぞれの方法の利点、トレードオフ、および要件の概要を示します。

方法	説明
	クエリ点に内挿される値は、最も近いサンプル グリッド点の値になります。 不連続 必要メモリ量は中程度 計算時間は最も速い 各次元に 2 つのグリッド点が必要
	クエリ点に内挿される値は、次のサンプル グリッド点の値になります。 不連続 メモリ要件および計算時間は最近傍の場合と同じ 1 次元の内挿にのみ使用可能 少なくとも 2 つのグリッド点が必要
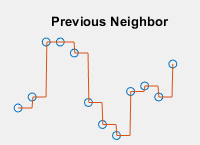
	クエリ点に内挿される値は、前のサンプル グリッド点の値になります。 不連続 メモリ要件および計算時間は最近傍の場合と同じ 1 次元の内挿にのみ使用可能 少なくとも 2 つのグリッド点が必要
	クエリ点に内挿される値は、対応する各次元における、隣接するグリッド点の値を使用した線形内挿に基づいて決定されます。 C0 連続 最近傍よりも多くのメモリと計算時間が必要 各次元に少なくとも 2 つのグリッド点が必要
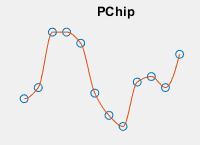
	クエリ点に内挿される値は、隣接するグリッド点の値を使用した区分的 3 次エルミート内挿多項式に基づいて決定されます。 C1 連続 線形よりも多くのメモリと長い計算時間が必要 1 次元の内挿にのみ使用可能 少なくとも 4 つのグリッド点が必要
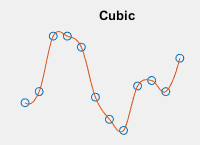
	クエリ点に内挿される値は、対応する各次元における、隣接するグリッド点の値を使用した 3 次内挿に基づいて決定されます。 C1 連続 線形よりも多くのメモリと長い計算時間が必要 グリッドが等間隔であることが必要 (各次元の間隔が同じである必要はない) 各次元に少なくとも 4 つの点が必要
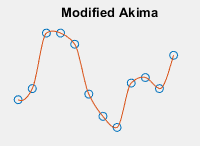
	クエリ点に内挿される値は、対応する各次元における隣接するグリッド点の値を使用した、最大 3 次の多項式の区分的関数に基づいて決定されます。オーバーシュートを回避するように Akima 式を修正したものです。 C1 連続 スプラインと同様のメモリ要件 計算時間は 3 次内挿よりも長いが、通常はスプラインより短い 各次元に少なくとも 2 つのグリッド点が必要
	クエリ点に内挿される値は、対応する各次元における、隣接するグリッド点の値を使用した 3 次内挿に基づいて決定されます。 C2 連続 3 次よりも多くのメモリと長い計算時間が必要 各次元に少なくとも 4 つの点が必要

参考

interp1 | interp2 | interp3 | interpn | griddedInterpolant

関連するトピック

• グリッド内挿でのイメージのリサンプリング
• 複数の 1 次元の値セットの内挿
• 3 次元グリッドにおける 2 次元選択の内挿