makima

修正 Akima 区分的 3 次エルミート内挿

構文

yq = makima(x,y,xq)

pp = makima(x,y)

説明

yq = makima(x,y,xq) は、サンプル点 x の値 y を使用して修正 Akima 内挿を実行し、クエリ点 xq における内挿値 yq を求めます。

pp = makima(x,y) は、ppval とスプライン ユーティリティ unmkpp で使用する区分的多項式構造体を返します。

例

余弦データの Akima 内挿

makima を使用して、等間隔でないサンプル点を通る余弦曲線を内挿します。

x = [0 1 2.5 3.6 5 7 8.1 10];
y = cos(x);
xq = 0:.25:10;
yq = makima(x,y,xq);
plot(x,y,'o',xq,yq,'--')

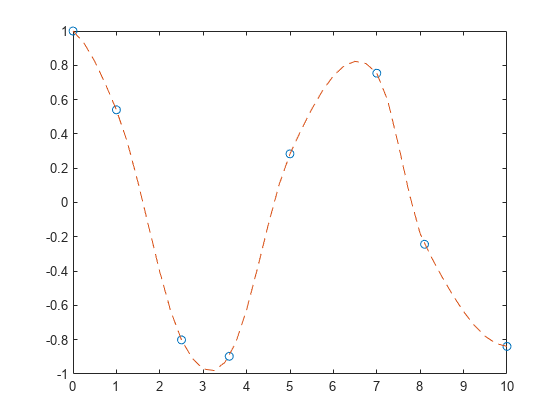
振動関数を使用する Akima アルゴリズムでは、局所的極値の近くで曲線の変動が少なくなります。この変動の少なさを補正するために、局所的極値付近のサンプル点を増加できます。

$\mathit{x}=6.5$ と $\mathit{x}=9$ の近くにサンプル点を追加し、内挿を再プロットします。

x = [0 1 2.5 3.6 5 6.5 7 8.1 9 10];
y = cos(x);
xq = 0:.25:10;
yq = makima(x,y,xq);
plot(x,y,'o',xq,yq,'--')

spline、pchip および makima によるデータ内挿

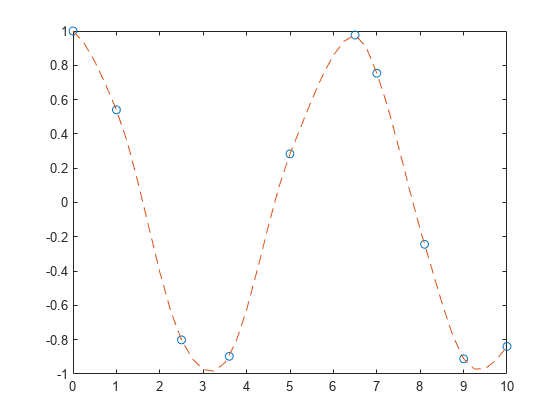
2 つの異なるデータ セットについて、spline、pchip、makima で生成された内挿結果を比較します。これらの関数はすべて、異なる形式の区分的 3 次エルミート内挿を実行します。内挿の傾きの計算方法が各関数で異なるため、基となるデータに変動の少ない領域やうねりがある場合の動作も異なります。

変動の少ない領域を接続するサンプル データの内挿結果を比較します。x の値のベクトル、点 y での関数値、クエリ点 xq を作成します。spline、pchip、および makima を使用して、クエリ点での内挿を計算します。比較のため、クエリ点での内挿関数値をプロットします。

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
m = makima(x,y,xq1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--')
legend('Sample Points','pchip','spline','makima','Location','SouthEast')

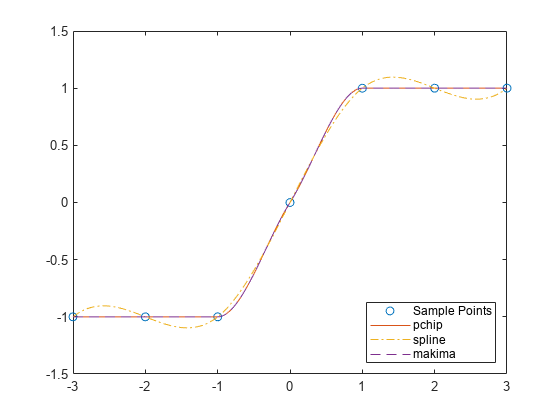
ここでは、pchip と makima が、オーバーシュートを起こさずに変動の少ない領域を正確に接続できるという点で同じような動作を示しています。

振動サンプル関数を使用して、2 回目の比較を行います。

x = 0:15;
y = besselj(1,x);
xq2 = 0:0.01:15;
p = pchip(x,y,xq2);
s = spline(x,y,xq2);
m = makima(x,y,xq2);
plot(x,y,'o',xq2,p,'-',xq2,s,'-.',xq2,m,'--')
legend('Sample Points','pchip','spline','makima')

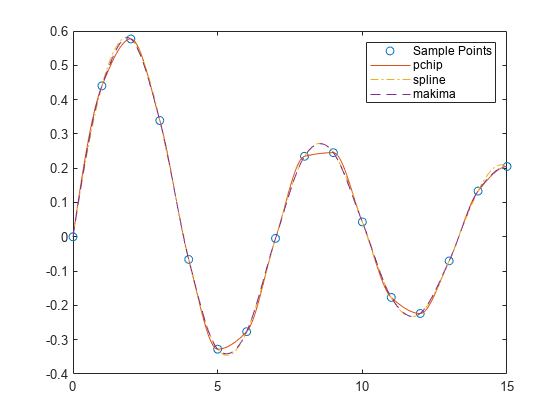
基となる関数が振動関数である場合、局所的極値付近での強引な変動が少ない pchip よりも、spline と makima の方が点の間の動きをより良好にキャプチャします。

区分的多項式構造体による Akima 内挿

サンプル点 x とそれらの点の値 y からなるベクトルを作成します。makima を使用して、そのデータの区分的多項式構造体を作成します。

x = -5:5;
y = [1 1 1 0 0 1 1 2 2 2 2];
pp = makima(x,y)

pp = struct with fields:
      form: 'pp'
    breaks: [-5 -4 -3 -2 -1 0 1 2 3 4 5]
     coefs: [10×4 double]
    pieces: 10
     order: 4
       dim: 1

この構造体には、データにわたる 10 個の 4 次多項式の情報が含まれます。pp.coefs(i,:) には、ブレークポイント [breaks(i) breaks(i+1)] で定義された領域で有効な多項式の係数が含まれます。

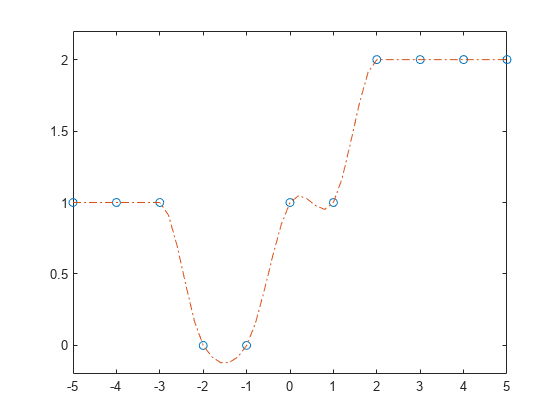
この構造体を ppval で使用して複数のクエリ点で内挿を評価してから、結果をプロットします。一定の点が 3 つ以上ある領域について、Akima アルゴリズムではそれらの点が直線で結ばれます。

xq = -5:0.2:5;
m = ppval(pp,xq);
plot(x,y,'o',xq,m,'-.')
ylim([-0.2 2.2])

入力引数

x — サンプル点

ベクトル

サンプル点。ベクトルとして指定します。ベクトル x は、データ y が与えられる時点を指定します。x の要素は一意でなければなりません。

データ型: single | double

y — サンプル点での関数値

ベクトル | 行列 | 配列

サンプル点での関数値。数値ベクトル、行列または配列として指定します。x と y は同じ長さでなければなりません。

y が行列または配列の場合、最後の次元の値 y(:,...,:,j) が x に一致させる値として使用されます。この場合、y の最後の次元は x と同じ長さでなければなりません。

データ型: single | double

xq — クエリ点

スカラー | ベクトル | 行列 | 配列

クエリ点。スカラー、ベクトル、行列または配列として指定します。xq で指定された点は、makima により計算された内挿関数値 yq の x 座標です。

データ型: single | double

出力引数

yq — クエリ点における内挿値

スカラー | ベクトル | 行列 | 配列

クエリ点における内挿値。スカラー、ベクトル、行列または配列として返されます。yq のサイズは、y と xq のサイズに関連しています。

• y がベクトルの場合、yq のサイズは xq と同じです。

• y がサイズ Ny = size(y) の配列の場合、以下の条件が適用されます。

  • xq がスカラーまたはベクトルの場合、size(yq) は [Ny(1:end-1) length(xq)] を返す。

  • xq が配列の場合、size(yq) は [Ny(1:end-1) size(xq)] を返す。

pp — 区分的多項式

構造体

区分的多項式。構造体として返されます。この構造体を関数 ppval とあわせて使用し、1 つ以上のクエリ点で内挿多項式を評価します。これらの構造体には次のフィールドがあります。

フィールド	説明
form	"区分的多項式" の場合 'pp'
breaks	長さ L+1 のベクトル。このベクトルには厳密に増加する要素があり、 L 個の区間のそれぞれについて開始と終了を表しています。
coefs	L 行 k 列の行列。各行 coefs(i,:) は、i 番目の区間 [breaks(i),breaks(i+1)] における k 次多項式の局所的な係数を含みます。
pieces	区分の数 (L)
order	多項式の次数
dim	ターゲットの次元

coefs の多項式係数は各区間の局所的な係数であるため、従来の多項方程式で係数を使用するには対応するノット区間の下限端点を減算しなければなりません。言い換えれば、区間 [x1,x2] の係数 [a,b,c,d] について、対応する多項式は次のようになります。

$$f\left(x\right)=a{\left(x-x_1\right)}^3+b{\left(x-x_1\right)}^2+c\left(x-x_1\right)+d.$$

詳細

修正 Akima 内挿

1 次元内挿の Akima アルゴリズム ([1] および [2] を参照) は、3 次内挿を実行して、連続 1 次微分 (C1) をもつ区分的多項式を生成します。このアルゴリズムは、過剰な局所のうねりを防ぎます。

$${\delta }_i=\frac{v_{i+1}-v_i}{x_{i+1}-x_i}$$ が区間 $$\left[x_i{x}_{i+1}\right)$$ の傾きである場合、サンプル点 $$x_i$$ における微分値 $$d_i$$ は隣接する傾きの加重平均です。

$$d_i=\frac{w_1}{w_1+w_2}{\delta }_{i-1}+\frac{w_2}{w_1+w_2}{\delta }_i.$$

Akima の元の式での重みは次のとおりです。

$$\begin{array}{l}{w}_1=\left|{\delta }_{i+1}-{\delta }_i\right|,\\ w_2=\left|{\delta }_{i-1}-{\delta }_{i-2}\right|.\end{array}$$

元の Akima アルゴリズムでは両側の点に等しい重みが指定されるため、うねりは均等に分割されます。

傾きが異なる 2 つの変動の少ない領域が一致する場合、元の Akima アルゴリズムに修正を加えると、傾きが 0 に近い側に多くの重みが割り当てられます。この修正によって水平に近い側が優先されます。これはより直観的であり、かつオーバーシュートが回避されます。特に、同一線上に連続する点が 3 点以上ある場合、このアルゴリズムではそれらが直線で結ばれ、これによりオーバーシュートが回避されます。

修正 Akima アルゴリズムで使用される重みは次のとおりです。

$$\begin{array}{l}{w}_1=\left|{\delta }_{i+1}-{\delta }_i\right|+\frac{\left|{\delta }_{i+1}+{\delta }_i\right|}{2},\\ w_2=\left|{\delta }_{i-1}-{\delta }_{i-2}\right|+\frac{\left|{\delta }_{i-1}+{\delta }_{i-2}\right|}{2}.\end{array}$$

spline アルゴリズムと比べると、Akima アルゴリズムでは生成されるうねりが少ないため、変動の少ない領域の間で急激に変化する場合への適用に適しています。pchip アルゴリズムと比べると、Akima アルゴリズムではそれほど強引な変動が少なくならないため、振動データにも適用することができます。

参照

[1] Akima, Hiroshi. "A new method of interpolation and smooth curve fitting based on local procedures." Journal of the ACM (JACM) , 17.4, 1970, pp. 589–602.

[2] Akima, Hiroshi. "A method of bivariate interpolation and smooth surface fitting based on local procedures." Communications of the ACM , 17.1, 1974, pp. 18–20.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• 入力 x は厳密に増加するものでなければなりません。

• コード生成では、値が NaN の y エントリは削除されません。

• pp = makima(x,y) 構文のコードを生成する場合は、MATLAB^® で関数 ppval に pp を入力できません。コード ジェネレーターで作成された pp 構造体から MATLAB の pp 構造体を作成するには、以下のように実行します。

  • コード生成では、unmkpp を使用して区分的多項式の詳細を MATLAB に返します。

  • MATLAB では、mkpp を使用して pp 構造体を作成します。

• xq を指定するときに、y が可変サイズであり、可変長ベクトルではない場合、生成コードでのベクトル出力の方向が MATLAB の方向と一致しない可能性があります。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

makima 関数は、GPU 配列を完全にサポートします。GPU 上で関数を実行するには、入力データを gpuArray (Parallel Computing Toolbox) として指定します。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意および制限:

• 構文 makima(x,y) は分散配列ではサポートされていません。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2019b で導入

参考

interp1 | spline | pchip | ppval

外部の Web サイト

• Cleve's Corner: Makima Piecewise Cubic Interpolation