ppval

区分的多項式の計算

構文

v = ppval(pp,xq)

説明

v = ppval(pp,xq) はクエリ点 xq での区分的多項式 pp を評価します。

例

多次多項式をもつ区分的多項式の作成

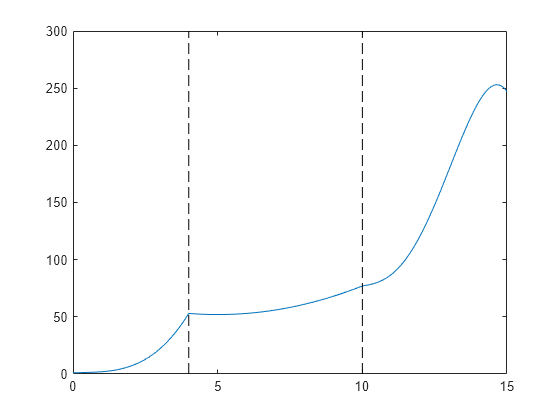
区間 [0,4] で 3 次多項式、区間 [4,10] で 2 次多項式、区間 [10,15] で 4 次多項式をもつ区分的多項式を作成します。

breaks = [0 4 10 15];
coefs = [0 1 -1 1 1; 0 0 1 -2 53; -1 6 1 4 77];
pp = mkpp(breaks,coefs)

pp = struct with fields:
      form: 'pp'
    breaks: [0 4 10 15]
     coefs: [3×5 double]
    pieces: 3
     order: 5
       dim: 1

区間 [0,15] にある多数の点でこの区分的多項式を評価し、結果をプロットします。縦の破線を、多項式同士が接しているブレーク ポイントにプロットします。

xq = 0:0.01:15;
plot(xq,ppval(pp,xq))
line([4 4],ylim,'LineStyle','--','Color','k')
line([10 10],ylim,'LineStyle','--','Color','k')

繰り返される区分をもつ区分的多項式の作成

2 つの 2 次多項式の間で切り替わる 4 つの区間をもつ区分的多項式を作成し、プロットします。

最初の 2 つのサブプロットは、2 次多項式とその正負を逆転したものを、区間 [-8,-4] および [-4,0] にシフトして示しています。この多項式は以下のようになります。

$$1-{(\frac{x}{2}-1)}^2=\frac{-x^2}{4}+x.$$

3 番目のサブプロットは、これら 2 つの 2 次式を 4 つの区間で交互に切り替えて作成した区分的多項式を示しています。多項式が接する点を示すために縦線が追加されます。

subplot(2,2,1)
cc = [-1/4 1 0]; 
pp1 = mkpp([-8 -4],cc);
xx1 = -8:0.1:-4; 
plot(xx1,ppval(pp1,xx1),'k-')

subplot(2,2,2)
pp2 = mkpp([-4 0],-cc);
xx2 = -4:0.1:0; 
plot(xx2,ppval(pp2,xx2),'k-')

subplot(2,1,2)
pp = mkpp([-8 -4 0 4 8],[cc;-cc;cc;-cc]);
xx = -8:0.1:8;
plot(xx,ppval(pp,xx),'k-')
hold on
line([-4 -4],ylim,'LineStyle','--')
line([0 0],ylim,'LineStyle','--')
line([4 4],ylim,'LineStyle','--')
hold off

入力引数

pp — 区分的多項式

構造体

区分的多項式。構造体として指定します。pp は、spline、pchip、makima、interp1、またはスプライン ユーティリティ関数 mkpp を使用して作成できます。

xq — クエリ点

ベクトル | 配列

クエリ点。ベクトルまたは配列として指定します。xq は ppval が区分的多項式を評価する点を指定します。

データ型: single | double

出力引数

v — クエリ点での区分的多項式の値

ベクトル | 行列 | 配列

クエリ点での区分的多項式の値。ベクトル、行列または配列として返されます。

pp に値が [d1,..,dr] の係数 (非スカラー係数値) がある場合、以下のようになります。

• xq が長さ N のベクトルである場合、v のサイズは [d1,...,dr,N] です。また、v(:,...,:,j) は xq(j) での値です。

• xq のサイズが [N1,...,Ns] である場合、v のサイズは [d1,...,dr,N1,...,Ns] で、v(:,...,:, j1,...,js) は xq(j1,...,js) での値です。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• 以下のステートメントの両方に該当する場合、出力 v のサイズは MATLAB^® と一致しません。

  • 入力 xx は、可変長ベクトルではない可変サイズの配列です。

  • xx は、実行時に行ベクトルになります。

  この場合、コード ジェネレーターは大きさが 1 の次元を削除しません。ただし、MATLAB は大きさが 1 の次元を削除する場合があります。

  たとえば、xx が :4 行 :5 列の配列であると仮定します (最初の次元は上限が 4 の可変サイズ、2 番目の次元は上限が 5 の可変サイズ)。また、ppval(pp,0) は 2 行 3 列の固定サイズの配列を返すと仮定します。v のサイズは 2×3×:4×:5 です。実行時には、size(x,1) =1 および size (x,2) = 5 と仮定します。生成されるコードで、size(v) は [2,3,1,5] となります。MATLAB では、サイズは [2,3,5] となります。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

ppval 関数は、GPU 配列を完全にサポートします。GPU 上で関数を実行するには、入力データを gpuArray (Parallel Computing Toolbox) として指定します。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

mkpp | unmkpp | spline | pchip