spline

3 次スプライン データ内挿

構文

s = spline(x,y,xq)

pp = spline(x,y)

説明

s = spline(x,y,xq) は、xq のクエリ点に対応する内挿値のベクトル s を返します。s の値は x と y の 3 次スプライン内挿により決定されます。

pp = spline(x,y) は、ppval とスプライン ユーティリティ unmkpp で使用する区分的多項式の構造体を返します。

例

正弦データのスプライン内挿

spline を使用して、等間隔のサンプル点に正弦曲線を内挿します。

x = [0 1 2.5 3.6 5 7 8.1 10];
y = sin(x);
xx = 0:.25:10;
yy = spline(x,y,xx);
plot(x,y,'o',xx,yy)

指定した端点の傾きによるスプライン内挿

端点の傾きが判明している場合に、固定または完全スプライン内挿を使用します。これは、2 つの追加要素 (1 つは始点に、1 つは終点に) を使用して値ベクトル $\mathit{y}$ を指定し、端点の傾きを定義することで行えます。

データ $\mathit{y}$ のベクトル、およびそのデータの $\mathit{x}$ 座標を使用した別のベクトルを作成します。

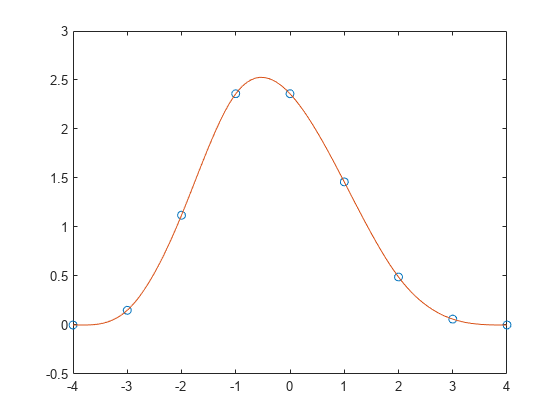
x = -4:4;
y = [0 .15 1.12 2.36 2.36 1.46 .49 .06 0];

spline を使用してデータを内挿し、結果をプロットします。2 つの追加の値 [0 y 0] を使用して 2 番目の入力を指定し、端点の傾きが両方ともゼロであると示します。ppval を使用して、内挿間隔の 101 点についてスプライン近似を評価します。

cs = spline(x,[0 y 0]);
xx = linspace(-4,4,101);
plot(x,y,'o',xx,ppval(cs,xx),'-');

3 次スプラインを使用した外挿

データ セットを外挿して人口増加を予測します。

1900 年から 1990 年までのアメリカ合衆国の国勢調査の実施年 (t) のベクトルと、それに対応した合衆国の百万人単位での人口 (p) を表す 2 つのベクトルを作成します。

t = 1900:10:1990;
p = [ 75.995  91.972  105.711  123.203  131.669 ...
     150.697 179.323  203.212  226.505  249.633 ];

3 次スプラインを使用して、2000 年の人口を外挿して予測します。

spline(t,p,2000)

ans = 
270.6060

角度データのスプライン内挿

上記は、o でマークした 5 個のデータ点 y(:,2),...,y(:,6) をもつ円のプロットを作成します。行列 y の列数は x より 2 列多くなっています。そのため、spline は y(:,1) と y(:,end) を端点の傾きとして使用します。円の始点と終点は点 (1,0) なので、この点は 2 回プロットされます。

x = pi*[0:.5:2]; 
y = [0  1  0 -1  0  1  0; 
     1  0  1  0 -1  0  1];
pp = spline(x,y);
yy = ppval(pp, linspace(0,2*pi,101));
plot(yy(1,:),yy(2,:),'-b',y(1,2:5),y(2,2:5),'or')
axis equal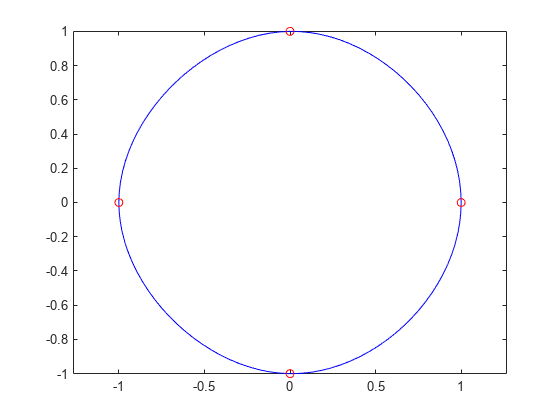

正弦データと余弦データのスプライン内挿

スプラインを使用して、細かいメッシュで関数をサンプリングします。

0 と 1 の間のいくつかの値に対して正弦曲線と余弦曲線を生成します。スプライン内挿を使用して、細かいメッシュで関数をサンプリングします。

x = 0:.25:1;
Y = [sin(x); cos(x)];
xx = 0:.1:1;
YY = spline(x,Y,xx);
plot(x,Y(1,:),'o',xx,YY(1,:),'-')
hold on
plot(x,Y(2,:),'o',xx,YY(2,:),':')
hold off

spline、pchip および makima によるデータ内挿

2 つの異なるデータ セットについて、spline、pchip、makima で生成された内挿結果を比較します。これらの関数はすべて、異なる形式の区分的 3 次エルミート内挿を実行します。内挿の傾きの計算方法が各関数で異なるため、基となるデータに変動の少ない領域やうねりがある場合の動作も異なります。

変動の少ない領域を接続するサンプル データの内挿結果を比較します。x の値のベクトル、点 y での関数値、クエリ点 xq を作成します。spline、pchip、および makima を使用して、クエリ点での内挿を計算します。比較のため、クエリ点での内挿関数値をプロットします。

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
m = makima(x,y,xq1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--')
legend('Sample Points','pchip','spline','makima','Location','SouthEast')

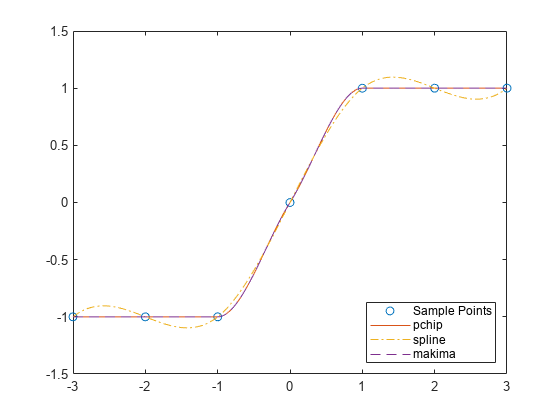
ここでは、pchip と makima が、オーバーシュートを起こさずに変動の少ない領域を正確に接続できるという点で同じような動作を示しています。

振動サンプル関数を使用して、2 回目の比較を行います。

x = 0:15;
y = besselj(1,x);
xq2 = 0:0.01:15;
p = pchip(x,y,xq2);
s = spline(x,y,xq2);
m = makima(x,y,xq2);
plot(x,y,'o',xq2,p,'-',xq2,s,'-.',xq2,m,'--')
legend('Sample Points','pchip','spline','makima')

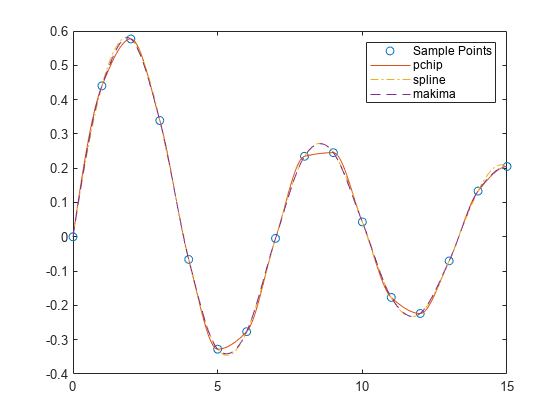
基となる関数が振動関数である場合、局所的極値付近での強引な変動が少ない pchip よりも、spline と makima の方が点の間の動きをより良好にキャプチャします。

入力引数

x — x 座標

ベクトル

x 座標。ベクトルとして指定します。ベクトル x は、データ y が与えられる時点を指定します。x の要素は一意でなければなりません。

3 次スプライン内挿には少なくとも 4 つの点が必要であり、2 つの点または 3 つの点が指定された場合は、それぞれ線形内挿または 2 次内挿にフォールバックします。

データ型: single | double

y — x 座標での関数値

ベクトル | 行列 | 配列

x 座標での関数値。数値ベクトル、行列または配列として指定します。x と y は通常は同じ長さですが、y は端点の傾きを指定するために x よりも厳密に 2 つ多い要素をもつことができます。

y が行列または配列の場合、最後の次元の値 y(:,...,:,j) が x に一致させる値として使用されます。この場合、y の最後の次元は x と同じ長さであるか、厳密に 2 つ多い要素がなければなりません。

3 次スプラインの端点の傾きは次の規則に従います。

• x および y が同じサイズのベクトルである場合、ノットなしの端点条件が使用される。

• x または y がスカラーである場合、長さがもう一方と同じになるように拡張され、ノットなしの端点条件が使用される。

• y が x より 2 つ多い値をもつベクトルの場合、spline は y の最初と最後の値を 3 次スプラインの端点の傾きとして使用する。たとえば、y がベクトルの場合、次のようになります。

  • y(2:end-1) は、x の各点での関数値を返す。

  • y(1) は、min(x) の位置の間隔について、開始時の傾きを返す。

  • y(end) は、max(x) の位置の間隔について、終了時の傾きを返す。

• 同様に、y が行列または length(x)+2 に等しい size(y,N) をもつ N 次元配列の場合、以下のようになります。

  • j = 1:length(x) について、y(:,...,:,j+1) は x の各点での関数値を返す。

  • y(:,:,...:,1) は、min(x) の位置の各間隔について、開始時の傾きを返す。

  • y(:,:,...:,end) は、max(x) の位置の各間隔について、終了時の傾きを返す。

データ型: single | double

xq — クエリ点

スカラー | ベクトル | 行列 | 配列

クエリ点。スカラー、ベクトル、行列または配列として指定します。xq で指定された点は、spline により計算された内挿関数値 yq の x 座標です。

データ型: single | double

出力引数

s — クエリ点における内挿値

スカラー | ベクトル | 行列 | 配列

クエリ点における内挿値。スカラー、ベクトル、行列または配列として返されます。

s のサイズは、y と xq のサイズに関連しています。

• y がベクトルの場合、s のサイズは xq と同じです。

• y がサイズ Ny = size(y) の配列の場合、以下の条件が適用されます。

  • xq がスカラーまたはベクトルの場合、size(s) は [Ny(1:end-1) length(xq)] を返す。

  • xq が配列の場合、size(s) は [Ny(1:end-1) size(xq)] を返す。

pp — 区分的多項式

構造体

区分的多項式。構造体として返されます。この構造体は関数 ppval とあわせて使用し、区分的多項式を 1 つ以上のクエリ点で評価します。これらの構造体には次のフィールドがあります。

フィールド	説明
form	"区分的多項式" の場合 'pp'
breaks	長さ L+1 のベクトル。このベクトルには厳密に増加する要素があり、 L 個の区間のそれぞれについて開始と終了を表しています。
coefs	L 行 k 列の行列。各行 coefs(i,:) は、i 番目の区間 [breaks(i),breaks(i+1)] における k 次多項式の局所的な係数を含みます。
pieces	区分の数 (L)
order	多項式の次数
dim	ターゲットの次元

coefs の多項式係数は各区間の局所的な係数であるため、従来の多項方程式で係数を使用するには対応するノット区間の下限端点を減算しなければなりません。言い換えれば、区間 [x1,x2] の係数 [a,b,c,d] について、対応する多項式は次のようになります。

$$f\left(x\right)=a{\left(x-x_1\right)}^3+b{\left(x-x_1\right)}^2+c\left(x-x_1\right)+d.$$

ヒント

• また、関数 interp1 を使用して、コマンド interp1(x,y,xq,'spline') でスプライン内挿を実行できます。spline が入力行列の行方向に内挿を実行する一方で、interp1 は入力行列の列方向に内挿を実行します。

アルゴリズム

三重対角線形方程式 (いくつかの右辺をもつ可能性があります) は、内挿するスプラインを作成するさまざまな 3 次多項式の係数を示すために必要な情報を基に解かれます。関数 spline は、関数 ppval、mkpp、unmkpp を使用します。これらのルーチンは、区分的多項式に機能する関数群です。より高度な機能へのアクセスについては、interp1 または Curve Fitting Toolbox™ スプライン関数を参照してください。

参照

[1] de Boor, Carl. A Practical Guide to Splines. Springer-Verlag, New York: 1978.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• 入力 x は厳密に増加するものでなければなりません。

• コード生成では、値が NaN の y エントリは削除されません。

• コード生成では、y の無限の端点の傾きについてエラーは報告されません。

• pp = spline(x,y) 構文のコードを生成する場合は、MATLAB^® で関数 ppval に pp を入力できません。コード ジェネレーターで作成された pp 構造体から MATLAB の pp 構造体を作成するには、以下のように実行します。

  • コード生成では、unmkpp を使用して区分的多項式の詳細を MATLAB に返します。

  • MATLAB では、mkpp を使用して pp 構造体を作成します。

• xq を指定するときに、y が可変サイズであり、可変長ベクトルではない場合、生成コードでのベクトル出力の方向が MATLAB の方向と一致しない可能性があります。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

spline 関数は GPU 配列入力をサポートしますが、次の使用上の注意および制限があります。

• 入力引数 y は非スパースでなければなりません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

interp1 | pchip | makima | ppval