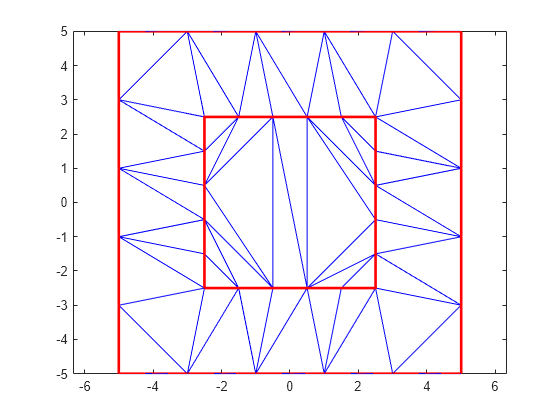
isInterior

Delaunay 三角形分割の内側にあるクエリ点

構文

TF = isInterior(DT)

説明

TF = isInterior(DT) は、2 次元の制約付き Delaunay 三角形分割の三角形が有界の幾何学的領域の内部にあるかどうかを示す logical 値の列ベクトルを返します。DT 内の三角形が領域内にある場合、対応する TF の要素は 1 (true)、そうでない場合は 0 (false) です。

例

指定された境界内の三角形

境界を指定し、その内部にある 2 次元の制約付き Delaunay 三角形分割の三角形を計算してプロットします。

形状が正方形フレームの幾何学的な領域を作成します。

outerprofile = [-5 -5; -3 -5; -1 -5;  1 -5; 
                 3 -5;  5 -5;  5 -3;  5 -1; 
                 5  1;  5  3;  5  5;  3  5; 
                 1  5; -1  5; -3  5; -5  5; 
                -5  3; -5  1; -5 -1; -5 -3];
innerprofile = outerprofile.*0.5;
P = [outerprofile; innerprofile];

エッジ制約を定義します。

outercons = [(1:19)' (2:20)'; 20 1;];
innercons = [(21:39)' (22:40)'; 40 21];
C = [outercons; innercons];

制約付き Delaunay 三角形分割を作成します。

DT = delaunayTriangulation(P,C);

三角形分割をプロットし、内側と外側の正方形を赤で強調表示します。

triplot(DT)  
hold on 
plot(DT.Points(innercons',1),DT.Points(innercons',2), ...
     '-r','LineWidth',2)  
plot(DT.Points(outercons',1),DT.Points(outercons',2), ...
     '-r','LineWidth',2)
axis equal  

内側と外側の正方形の間にある三角形のみをプロットし、内側と外側の正方形を赤で強調表示します。

figure
TF = isInterior(DT);
triplot(DT.ConnectivityList(TF,:),DT.Points(:,1),DT.Points(:,2))  
hold on
plot(DT.Points(outercons',1),DT.Points(outercons',2), ...
     '-r','LineWidth',2)
plot(DT.Points(innercons',1),DT.Points(innercons',2), ...
     '-r','LineWidth',2)
axis equal

入力引数

DT — 制約付き Delaunay 三角形分割

スカラー

制約付き Delaunay 三角形分割。有界の幾何学的領域を定義する一連の制約付きエッジをもつ、スカラーの 2 次元 delaunayTriangulation オブジェクトとして指定します。有界領域とは、交差もオーバーラップもしない複数の制約付きエッジで囲まれた領域です。

データ型: delaunayTriangulation

ヒント

• isInterior は、境界の制約が交差するかオーバーラップする場合に、不正確な結果または矛盾する結果を生成することがあります。この動作を回避するには、1 つ以上の閉じた境界を形成する、交差もオーバーラップもしない複数の制約を使用します。境界の制約が、交差もオーバーラップもせずに入れ子にされている場合、境界全体で内部と外部のステータスが交互に切り替わります。

拡張機能

スレッドベースの環境
MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

バージョン履歴

R2013a で導入

参考

delaunayTriangulation