fit

fitobject = fit(x,y,fitType) は fitType で指定されたモデルを使用し、x および y についてデータの近似を作成します。

fitobject = fit([x,y],z,fitType) は、ベクトル x、y、z についてデータの曲面近似を作成します。

fitobject = fit(x,y,fitType,fitOptions) は、fitOptions オブジェクトで指定されたアルゴリズムオプションを使用してデータの近似を作成します。

fitobject = fit(x,y,fitType,Name=Value) は、ライブラリモデル fitType と、1 つ以上の Name=Value ペア引数で指定された追加オプションを使用してデータの近似を作成します。fitoptions を使用すると、特定のライブラリモデルの使用可能なプロパティ名と既定の値を表示できます。

[fitobject,gof] = fit(x,y,fitType) は、構造体 gof の適合度の統計量を返します。

[fitobject,gof,output] = fit(x,y,fitType) は、構造体 output の近似アルゴリズム情報を返します。

例

2 次曲線による近似

census サンプルデータセットを読み込みます。

load census;

ベクトル pop と cdate には、人口サイズと国勢調査の実施年に関するデータがそれぞれ含まれています。

人口データに 2 次曲線を当てはめます。

f=fit(cdate,pop,'poly2')

f = 
     Linear model Poly2:
     f(x) = p1*x^2 + p2*x + p3
     Coefficients (with 95% confidence bounds):
       p1 =    0.006541  (0.006124, 0.006958)
       p2 =      -23.51  (-25.09, -21.93)
       p3 =   2.113e+04  (1.964e+04, 2.262e+04)

f に 95% 信頼限界の係数推定値を含む近似の結果が格納されます。

f の近似をデータの散布図と一緒にプロットします。

plot(f,cdate,pop)

Figure contains an axes object. The axes object with xlabel x, ylabel y contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent data, fitted curve.

プロットは、近似曲線が人口データに密接に追従していることを示しています。

多項式曲面による近似

franke サンプルデータセットを読み込みます。

load franke

ベクトル x、y、および z には、フランケの二変量テスト関数から生成され、ノイズとスケーリングが追加されたデータが格納されています。

データに多項式曲面を当てはめます。x の項の次数を 2、y の項の次数を 3 と指定します。

sf = fit([x, y],z,'poly23')

     Linear model Poly23:
     sf(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y 
                    + p12*x*y^2 + p03*y^3
     Coefficients (with 95% confidence bounds):
       p00 =       1.118  (0.9149, 1.321)
       p10 =  -0.0002941  (-0.000502, -8.623e-05)
       p01 =       1.533  (0.7032, 2.364)
       p20 =  -1.966e-08  (-7.084e-08, 3.152e-08)
       p11 =   0.0003427  (-0.0001009, 0.0007863)
       p02 =      -6.951  (-8.421, -5.481)
       p21 =   9.563e-08  (6.276e-09, 1.85e-07)
       p12 =  -0.0004401  (-0.0007082, -0.0001721)
       p03 =       4.999  (4.082, 5.917)

sf に 95% 信頼限界の係数推定値を含む近似の結果が格納されます。

sf の近似をデータの散布図と一緒にプロットします。

plot(sf,[x,y],z)

Figure contains an axes object. The axes object contains 2 objects of type surface, line. One or more of the lines displays its values using only markers

MATLAB テーブル内の変数を使用した曲面近似

franke データを読み込み、MATLAB® テーブルに変換します。

load franke
T = table(x,y,z);

テーブル内の変数を関数 fit への入力として指定し、近似をプロットします。

f = fit([T.x, T.y],T.z,'linearinterp');
plot( f, [T.x, T.y], T.z )

Figure contains an axes object. The axes object contains 2 objects of type surface, line. One or more of the lines displays its values using only markers

近似前の近似オプションと近似タイプの作成

データを読み込んでプロットし、関数 fittype および fitoptions を使用して近似オプションと近似タイプを作成してから、近似を作成してプロットします。

census.mat のデータを読み込んでプロットします。

load census
plot(cdate,pop,'o')

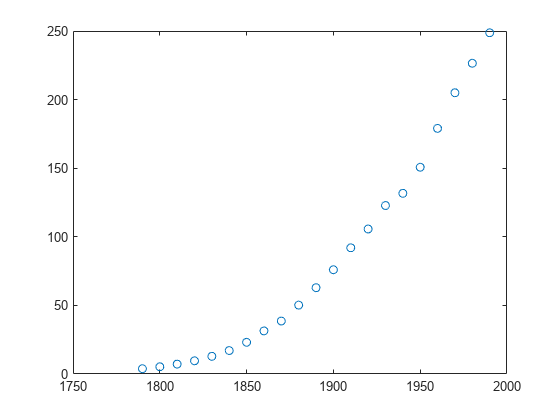
Figure contains an axes object. The axes contains a line object which displays its values using only markers.

カスタム非線形モデル $y = a (x - b)^{n}$ について近似オプションオブジェクトと近似タイプを作成します。ここで、a と b は係数、n は問題依存のパラメーターです。

fo = fitoptions('Method','NonlinearLeastSquares',...
               'Lower',[0,0],...
               'Upper',[Inf,max(cdate)],...
               'StartPoint',[1 1]);
ft = fittype('a*(x-b)^n','problem','n','options',fo);

近似オプションと n = 2 の値を使用して、データに当てはめます。

[curve2,gof2] = fit(cdate,pop,ft,'problem',2)

curve2 = 
     General model:
     curve2(x) = a*(x-b)^n
     Coefficients (with 95% confidence bounds):
       a =    0.006092  (0.005743, 0.006441)
       b =        1789  (1784, 1793)
     Problem parameters:
       n =           2

gof2 = struct with fields:
           sse: 246.1543
       rsquare: 0.9980
           dfe: 19
    adjrsquare: 0.9979
          rmse: 3.5994

近似オプションと n = 3 の値を使用して、データに当てはめます。

[curve3,gof3] = fit(cdate,pop,ft,'problem',3)

curve3 = 
     General model:
     curve3(x) = a*(x-b)^n
     Coefficients (with 95% confidence bounds):
       a =   1.359e-05  (1.245e-05, 1.474e-05)
       b =        1725  (1718, 1731)
     Problem parameters:
       n =           3

gof3 = struct with fields:
           sse: 232.0058
       rsquare: 0.9981
           dfe: 19
    adjrsquare: 0.9980
          rmse: 3.4944

近似結果をデータと共にプロットします。

hold on
plot(curve2,'m')
plot(curve3,'c')
legend('Data','n=2','n=3')
hold off

Figure contains an axes object. The axes object with xlabel x, ylabel y contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, n=2, n=3.

複数の多項式の近似

carbon12alpha 核反応サンプルデータセットを読み込みます。

load carbon12alpha

angle は、放出角度 (ラジアン単位) のベクトルです。counts は、angle 内の角度に対応する生のアルファ粒子数のベクトルです。

角度に対してプロットされた粒子数の散布図を表示します。

scatter(angle,counts)

Figure contains an axes object. The axes object contains an object of type scatter.

散布図は、粒子数が、角度の増加に合わせて、0 と 4.5 の間で振動していることを示しています。多項式モデルをデータに当てはめるため、fitType 入力引数に "poly#" を指定します。ここで、# は 1 から 9 の任意の整数です。最大 9 次のモデルを当てはめられます。詳細については、曲線近似または曲面近似のライブラリモデルのリストを参照してください。

5 次、7 次、9 次の多項式を核反応データに当てはめます。近似ごとに、適合度の統計量を返します。

[f5,gof5] = fit(angle,counts,"poly5");
[f7,gof7] = fit(angle,counts,"poly7");
[f9,gof9] = fit(angle,counts,"poly9");

関数linspaceを使用して、0 と 4.5 の間のクエリ点のベクトルを生成します。クエリ点で多項式近似を評価し、それを核反応データと一緒にプロットします。

xq = linspace(0,4.5,1000);

figure
hold on
scatter(angle,counts,"k")
plot(xq,f5(xq))
plot(xq,f7(xq))
plot(xq,f9(xq))
ylim([-100,550])
legend("original data","fifth-degree polynomial","seventh-degree polynomial","ninth-degree polynomial")

Figure contains an axes object. The axes object contains 4 objects of type scatter, line. These objects represent original data, fifth-degree polynomial, seventh-degree polynomial, ninth-degree polynomial.

プロットは、9 次多項式が最も密接にデータに追従していることを示しています。

関数struct2tableを使用して、近似ごとに適合度の統計量を表示します。

gof = struct2table([gof5 gof7 gof9],RowNames=["f5" "f7" "f9"])

gof=3×5 table
             sse        rsquare    dfe    adjrsquare     rmse 
          __________    _______    ___    __________    ______

    f5    1.0901e+05    0.54614    18      0.42007       77.82
    f7         32695    0.86387    16      0.80431      45.204
    f9        3660.2    0.98476    14      0.97496      16.169

9 次多項式近似の二乗和誤差 (SSE) は、5 次および 7 次の近似の SSE より小さくなっています。この結果から、9 次多項式が最も密接にデータに追従していることが確認されます。

正規化とロバストのオプションの指定

census サンプルデータセットを読み込みます。3 次多項式を当てはめ、Normalize (センタリングとスケーリング) と Robust の近似オプションを指定します。

load census;
f = fit(cdate,pop,'poly3','Normalize','on','Robust','Bisquare')

f = 
     Linear model Poly3:
     f(x) = p1*x^3 + p2*x^2 + p3*x + p4
       where x is normalized by mean 1890 and std 62.05
     Coefficients (with 95% confidence bounds):
       p1 =     -0.4619  (-1.895, 0.9707)
       p2 =       25.01  (23.79, 26.22)
       p3 =       77.03  (74.37, 79.7)
       p4 =       62.81  (61.26, 64.37)

近似をプロットします。

plot(f,cdate,pop)

ファイルで定義された曲線による近似

ファイルに関数を定義し、それを使用して近似タイプを作成し曲線で近似します。

関数を MATLAB^® ファイルに定義します。

function y = piecewiseLine(x,a,b,c,d,k)
% PIECEWISELINE   A line made of two pieces
% that is not continuous.

y = zeros(size(x));

% This example includes a for-loop and if statement
% purely for example purposes.
for i = 1:length(x)
    if x(i) < k,
        y(i) = a + b.* x(i);
    else
        y(i) = c + d.* x(i);
    end
end
end

ファイルを保存します。

データを定義し、関数 piecewiseLine を指定して近似タイプを作成します。その近似タイプ ft を使用して近似を作成し、結果をプロットします。

x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;...
0.96;0.96;0.16;0.97;0.96];
y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;...
0.15;-0.046;0.17;-0.091;-0.071];
ft = fittype( 'piecewiseLine( x, a, b, c, d, k )' )
f = fit( x, y, ft, 'StartPoint', [1, 0, 1, 0, 0.5] )
plot( f, x, y )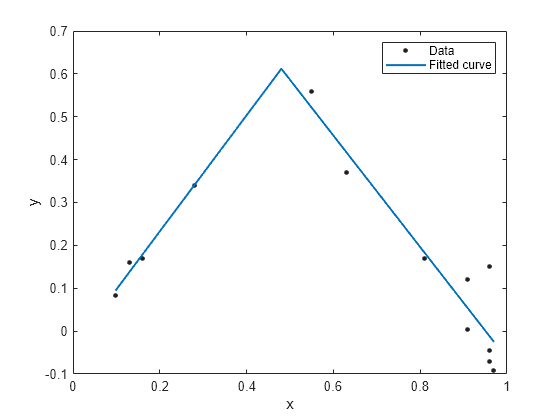

近似からの点の除外

データを読み込み、除外する点を指定してカスタム式で近似します。結果をプロットします。

データを読み込み、カスタム式と開始点を定義します。

[x, y] = titanium;

gaussEqn = 'a*exp(-((x-b)/c)^2)+d'

gaussEqn = 
'a*exp(-((x-b)/c)^2)+d'

startPoints = [1.5 900 10 0.6]

startPoints = 1×4

    1.5000  900.0000   10.0000    0.6000

カスタム式と開始点を使用して 2 つの近似を作成します。インデックスベクトルと式を使用して 2 組の異なる除外点を定義します。Exclude を使用して近似から外れ値を削除します。

f1 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', [1 10 25])

f1 = 
     General model:
     f1(x) = a*exp(-((x-b)/c)^2)+d
     Coefficients (with 95% confidence bounds):
       a =       1.493  (1.432, 1.554)
       b =       897.4  (896.5, 898.3)
       c =        27.9  (26.55, 29.25)
       d =      0.6519  (0.6367, 0.6672)

f2 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', x < 800)

f2 = 
     General model:
     f2(x) = a*exp(-((x-b)/c)^2)+d
     Coefficients (with 95% confidence bounds):
       a =       1.494  (1.41, 1.578)
       b =       897.4  (896.2, 898.7)
       c =       28.15  (26.22, 30.09)
       d =      0.6466  (0.6169, 0.6764)

両方の近似をプロットします。

plot(f1,x,y)
title('Fit with data points 1, 10, and 25 excluded')

Figure contains an axes object. The axes object with title Fit with data points 1, 10, and 25 excluded, xlabel x, ylabel y contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent data, fitted curve.

figure
plot(f2,x,y)
title('Fit with data points excluded such that x < 800')

Figure contains an axes object. The axes object with title Fit with data points excluded such that x < 800, xlabel x, ylabel y contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent data, fitted curve.

点の除外と除外したデータを示す近似のプロット

除外する点を関数 fit への入力として指定する前に、それらの点を変数として定義できます。以下の手順では、前述の例の近似を再作成し、除外した点をデータと近似と共にプロットします。

データを読み込み、カスタム式と開始点を定義します。

[x, y] = titanium;

gaussEqn = 'a*exp(-((x-b)/c)^2)+d'

gaussEqn = 
'a*exp(-((x-b)/c)^2)+d'

startPoints = [1.5 900 10 0.6]

startPoints = 1×4

    1.5000  900.0000   10.0000    0.6000

インデックスベクトルと式を使用して、除外する 2 組の点を定義します。

exclude1 = [1 10 25];
exclude2 = x < 800;

カスタム式、開始点および 2 組の異なる除外点を使用して 2 つの近似を作成します。

f1 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', exclude1);
f2 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', exclude2);

両方の近似をプロットし、除外したデータを強調表示します。

plot(f1,x,y,exclude1)
title('Fit with data points 1, 10, and 25 excluded')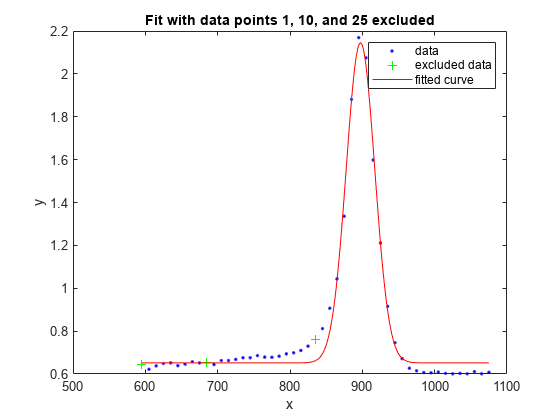

Figure contains an axes object. The axes object with title Fit with data points 1, 10, and 25 excluded, xlabel x, ylabel y contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent data, excluded data, fitted curve.

figure; 
plot(f2,x,y,exclude2)
title('Fit with data points excluded such that x < 800')

Figure contains an axes object. The axes object with title Fit with data points excluded such that x < 800, xlabel x, ylabel y contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent data, excluded data, fitted curve.

除外点を使用する曲面近似の例として、曲面データを読み込み、除外するデータを指定して近似を作成しプロットします。

load franke
f1 = fit([x y],z,'poly23', 'Exclude', [1 10 25]);
f2 = fit([x y],z,'poly23', 'Exclude', z > 1);

figure
plot(f1, [x y], z, 'Exclude', [1 10 25]);
title('Fit with data points 1, 10, and 25 excluded')

Figure contains an axes object. The axes object with title Fit with data points 1, 10, and 25 excluded contains 3 objects of type surface, line. One or more of the lines displays its values using only markers

figure
plot(f2, [x y], z, 'Exclude', z > 1);
title('Fit with data points excluded such that z > 1')

Figure contains an axes object. The axes object with title Fit with data points excluded such that z > 1 contains 3 objects of type surface, line. One or more of the lines displays its values using only markers

外挿法の比較

関数 membrane とrandnを使用してノイズを含むデータを生成します。

n = 41;
M = membrane(1,20)+0.02*randn(n);
[X,Y] = meshgrid(1:n);

行列 M には、ノイズを追加した L 型膜のデータが格納されています。行列 X と Y には、M 内の対応する要素の行と列のインデックス値がそれぞれ格納されています。

データの表面プロットを表示します。

figure(1)
surf(X,Y,M)

Figure contains an axes object. The axes object contains an object of type surface.

プロットは、しわのある L 型膜を示します。膜内のしわは、データ内のノイズが原因で生じています。

線形内挿を使用して、2 つの曲面をしわのある膜に当てはめます。最初の曲面には、線形外挿法を指定します。2 番目の曲面には、外挿法として最近傍を指定します。

flinextrap = fit([X(:),Y(:)],M(:),"linearinterp",ExtrapolationMethod="linear");
fnearextrap = fit([X(:),Y(:)],M(:),"linearinterp",ExtrapolationMethod="nearest");

関数meshgridを使用して X と Y のデータの凸包の外側に拡張しているクエリ点で近似を評価し、外挿法の違いを調べます。

[Xq,Yq] = meshgrid(-10:50);

Zlin = flinextrap(Xq,Yq);
Znear = fnearextrap(Xq,Yq);

評価された近似をプロットします。

figure(2)
surf(Xq,Yq,Zlin)
title("Linear Extrapolation")
xlabel("X")
ylabel("Y")
zlabel("M")

Figure contains an axes object. The axes object with title Linear Extrapolation, xlabel X, ylabel Y contains an object of type surface.

figure(3)
surf(Xq,Yq,Znear)
title("Nearest Neighbor Extrapolation")
xlabel("X")
ylabel("Y")
zlabel("M")

Figure contains an axes object. The axes object with title Nearest Neighbor Extrapolation, xlabel X, ylabel Y contains an object of type surface.

線形外挿法は、凸包の外側にスパイクを生成します。スパイクを形成している平面セグメントは、凸包の境界上の点での勾配に従います。最近傍外挿法は、境界上のデータを使って各方向に曲面を拡張します。この外挿法は、境界を再現する波形を生成します。

適合度の統計量と近似アルゴリズムの情報の取得

平滑化スプライン曲線を当てはめ、適合度の統計量と近似アルゴリズムに関する情報を返します。

enso サンプルデータセットを読み込みます。enso サンプルデータセットには、イースター島とオーストラリアのダーウィンの月間平均大気圧の差に関するデータが含まれています。

load enso;

month と pressure のデータに平滑化スプライン曲線を当てはめ、適合度の統計量と output 構造体を返します。

[curve,gof,output] = fit(month,pressure,"smoothingspline");

当てはめた曲線を、曲線の当てはめに使用したデータと共にプロットします。

plot(curve,month,pressure);
xlabel("Month");
ylabel("Pressure");

Figure contains an axes object. The axes object with xlabel Month, ylabel Pressure contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent data, fitted curve.

x データ (month) に対する残差をプロットします。

plot(curve,month,pressure,"residuals")
xlabel("Month")
ylabel("Residuals")

Figure contains an axes object. The axes object with xlabel Month, ylabel Residuals contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent data, zero line.

output 構造体の residuals のデータを使用して、y データ (pressure) に対する残差をプロットします。output の residuals フィールドにアクセスするには、ドット表記を使用します。

residuals = output.residuals;
plot( pressure,residuals,".")
xlabel("Pressure")
ylabel("Residuals")

Figure contains an axes object. The axes object with xlabel Pressure, ylabel Residuals contains a line object which displays its values using only markers.

単項指数関数による近似

指数関数的トレンドのデータを生成し、指数モデルの曲線近似ライブラリにある最初の方程式 (単項指数関数) を使用してそのデータに当てはめます。結果をプロットします。

x = (0:0.2:5)';
y = 2*exp(-0.2*x) + 0.5*randn(size(x));
f = fit(x,y,'exp1');
plot(f,x,y)

無名関数を使用したカスタムモデルによる近似

無名関数を使用すると、他のデータを関数 fit に簡単に渡せます。

データを読み込み、無名関数を定義する前に Emax を 1 に設定します。

data = importdata( 'OpioidHypnoticSynergy.txt' );
Propofol      = data.data(:,1);
Remifentanil  = data.data(:,2);
Algometry     = data.data(:,3);
Emax = 1;

モデル方程式を無名関数として定義します。

Effect = @(IC50A, IC50B, alpha, n, x, y) ...
    Emax*( x/IC50A + y/IC50B + alpha*( x/IC50A )...
    .* ( y/IC50B ) ).^n ./(( x/IC50A + y/IC50B + ...
    alpha*( x/IC50A ) .* ( y/IC50B ) ).^n  + 1);

無名関数 Effect を関数 fit への入力として使用し、結果をプロットします。

AlgometryEffect = fit( [Propofol, Remifentanil], Algometry, Effect, ...
    'StartPoint', [2, 10, 1, 0.8], ...
    'Lower', [-Inf, -Inf, -5, -Inf], ...
    'Robust', 'LAR' )
plot( AlgometryEffect, [Propofol, Remifentanil], Algometry )

無名関数の使用例と他の近似用カスタムモデルの詳細については、関数 fittype を参照してください。

開始点と範囲を設定するための係数順序の確認

プロパティ Upper、Lower、StartPoint については、係数のエントリ順序を確認する必要があります。

近似タイプを作成します。

ft = fittype('b*x^2+c*x+a');

関数 coeffnames を使用して係数名と順序を取得します。

coeffnames(ft)

ans = 3x1 cell
    {'a'}
    {'b'}
    {'c'}

これは、fittype を使用して ft を作成するときに使用する式の係数の順序とは異なることに注意してください。

データを読み込み、近似を作成し、開始点を設定します。

load enso
fit(month,pressure,ft,'StartPoint',[1,3,5])

ans = 
     General model:
     ans(x) = b*x^2+c*x+a
     Coefficients (with 95% confidence bounds):
       a =       10.94  (9.362, 12.52)
       b =   0.0001677  (-7.985e-05, 0.0004153)
       c =     -0.0224  (-0.06559, 0.02079)

これにより、a = 1、b = 3、c = 5 のように、係数に初期値が代入されます。

または、近似オプションを取得し、開始点と下限を設定してから、新しいオプションを使用して再近似することもできます。

options = fitoptions(ft)

options = 
  nlsqoptions with properties:

       StartPoint: []
            Lower: []
            Upper: []
        Algorithm: 'Trust-Region'
    DiffMinChange: 1.0000e-08
    DiffMaxChange: 0.1000
          Display: 'Notify'
      MaxFunEvals: 600
          MaxIter: 400
           TolFun: 1.0000e-06
             TolX: 1.0000e-06
           Robust: 'Off'
        Normalize: 'off'
          Exclude: []
          Weights: []
           Method: 'NonlinearLeastSquares'

options.StartPoint = [10 1 3];
options.Lower = [0 -Inf 0];
fit(month,pressure,ft,options)

ans = 
     General model:
     ans(x) = b*x^2+c*x+a
     Coefficients (with 95% confidence bounds):
       a =       10.23  (9.448, 11.01)
       b =   4.335e-05  (-1.82e-05, 0.0001049)
       c =   5.523e-12  (fixed at bound)

入力引数

`x` — 近似対象のデータ
行列

近似対象のデータ。1 列 (曲線近似) または 2 列 (曲面近似) の行列として指定します。tablename.varname を使用して MATLAB テーブル内の変数を指定できます。Inf または NaN を含めることはできません。複素数データの実数部のみが近似に使用されます。

例: x

例: [x,y]

データ型: double

`y` — 近似対象のデータ
ベクトル

近似対象のデータ。x と同じ行数の列ベクトルとして指定します。tablename.varname を使用して MATLAB テーブル内の変数を指定できます。Inf または NaN を含めることはできません。複素数データの実数部のみが近似に使用されます。

データが列ベクトル形式でない場合は、prepareCurveData または prepareSurfaceData を使用します。

データ型: double

`z` — 近似対象のデータ
ベクトル

データが列ベクトル形式でない場合は、prepareSurfaceData を使用します。たとえば、3 つの行列がある場合やデータがグリッドベクトル形式である場合が該当します。ただし、length(X) = n, length(Y) = m および size(Z) = [m,n] とします。

データ型: double

`fitType` — 近似に使用するモデルタイプ
文字ベクトル | string スカラー | string 配列 | 文字ベクトルの cell 配列 | 無名関数 | `fittype`

近似に使用するモデルタイプ。ライブラリモデル名または MATLAB 式を表す文字ベクトルまたは string スカラー、線形モデル項の string 配列または線形モデル項の文字ベクトルの cell 配列、無名関数、あるいは関数 fittype により作成された fittype として指定します。fittype への有効な最初の入力のいずれかを fit への入力として使用できます。

ライブラリモデル名の一覧については、モデルの名前と方程式を参照してください。

カスタムモデルを当てはめるには、MATLAB 式、線形モデル項の cell 配列、または無名関数を使用します。関数 fittype を使用して fittype を作成し、それを入力引数 fitType の値として使用することもできます。例については、無名関数を使用したカスタムモデルによる近似を参照してください。線形モデル項を使用する例については、関数 fittype を参照してください。

例: "poly2"

`fitOptions` — アルゴリズムオプション
`fitoptions`

関数 fitoptions を使用して構成されたアルゴリズムオプションです。近似オプションにおける名前と値のペア引数の指定に代わるものです。

名前と値の引数

引数の任意のペアを Name1=Value1,...,NameN=ValueN のように指定します。Name は引数名、Value は対応する値です。名前と値の引数は、他の引数より後に指定されている必要があります。ただし、各ペアの順序は任意です。

R2021a 以前では、それぞれの名前と値をコンマで区切り、Name を引用符で囲みます。

例: Lower=[0,0],Upper=[Inf,max(x)],StartPoint=[1 1] は近似法、範囲、開始点を指定します。

すべての近似法のオプション

`Normalize` — データのセンタリングとスケーリングを行うオプション
`'off'` (既定値) | `'on'`

データのセンタリングとスケーリングを行うオプション。'Normalize' と 'on' または 'off' で構成されるコンマ区切りのペアとして指定します。

データ型: char

`Exclude` — 近似から除外する点
式 | インデックスベクトル | logical ベクトル | 空

近似から除外する点。'Exclude' と次のいずれかで構成されるコンマ区切りのペアとして指定します。

logical ベクトルを記述する式。たとえば、x > 10。
除外する点にインデックス付けする整数のベクトル。たとえば、[1 10 25]。
excludedata によって作成され、true が外れ値を表す、すべてのデータ点についての logical ベクトル。

例については、近似からの点の除外を参照してください。

データ型: logical | double

`Weights` — 近似の重み
[ ] (既定値) | ベクトル

近似の重み。'Weights' と、応答データ y (曲線) または z (曲面) と同じサイズのベクトルで構成されるコンマ区切りのペアとして指定します。

データ型: double

`problem` — 問題依存の定数への代入値
cell 配列 | double

問題依存の定数への代入値。'problem' と、問題依存の定数ごとに 1 つの要素をもつ cell 配列で構成されるコンマ区切りのペアとして指定します。詳細については、fittype を参照してください。

データ型: cell | double

平滑化オプション

`SmoothingParam` — 平滑化パラメーター
範囲 (0,1) 内のスカラー値

平滑化パラメーター。'SmoothingParam' と、0 と 1 の間のスカラー値で構成されるコンマ区切りペアとして指定します。既定値はデータセットによって異なります。近似タイプが smoothingspline の場合のみ使用できます。

データ型: double

`Span` — 局所回帰で使用するデータ点の割合
0.25 (既定値) | 範囲 (0,1) 内のスカラー値

局所回帰で使用するデータ点の割合。'Span' と、0 と 1 の間のスカラー値で構成されるコンマ区切りペアとして指定します。近似タイプが lowess または loess の場合のみ使用できます。

データ型: double

内挿オプション

`ExtrapolationMethod` — 外挿法
`"auto"` (既定値) | `"none"` | `"linear"` | `"nearest"` | `"thinplate"` | `"biharmonic"` | `"pchip"` | `"cubic"`

内挿近似の外挿法。次の値のいずれかとして指定します。

値	説明	サポートされる近似
`"auto"`	すべてのタイプの内挿近似に対する既定値。`ExtrapolationMethod` を `"auto"` に設定すると、近似を行う際に外挿法が自動的に割り当てられます。	すべてのタイプの内挿近似、`cubicspline` 曲線近似
`"none"`	外挿なし。近似データの凸包の外側のクエリ点を `NaN` と評価します。 `fit` は、`cubicinterp` 曲面近似および `linearinterp` 曲面近似の `ExtrapolationMethod` が `"auto"` に設定されている場合に、外挿法を `"none"` に設定します。	曲線近似 — `cubicspline`、`pchipinterp` 曲線近似および曲面近似 — `cubicinterp`、`linearinterp`、`nearestinterp`
`"linear"`	境界勾配に基づく線形外挿。 `fit` は、`"linearinterp"` 曲線近似の `ExtrapolationMethod` が `"auto"` に設定されている場合に、外挿法を `"linear"` に設定します。	曲面近似 — `cubicinterp`、`nearestinterp` 曲線近似および曲面近似 — `linearinterp`
`"nearest"`	最近傍外挿。この手法は、近似データの凸包の境界上の最も近い点の値に評価します。 `fit` は、`"nearestinterp"` 曲線近似および曲面近似の `ExtrapolationMethod` が `"auto"` に設定されている場合に、外挿法を `"nearest"` に設定します。	曲線近似 — `cubicspline`、`pchipinterp` 曲線近似および曲面近似 — `cubicinterp`、`linearinterp`、`nearestinterp`
`"thinplate"`	薄板スプライン外挿。この手法は、近似データの凸包の外側に薄板内挿スプラインを拡張します。詳細については、`tpaps` を参照してください。 `fit` は、`"thinplateinterp"` 曲面近似の `ExtrapolationMethod` が `"auto"` に設定されている場合に、外挿法を `"thinplate"` に設定します。	曲面近似 — `thinplateinterp`
`"biharmonic"`	重調和スプライン外挿。この手法は、近似データの凸包の外側に重調和内挿スプラインを拡張します。 `fit` は、`"biharmonicinterp"` 曲面近似の `ExtrapolationMethod` が `"auto"` に設定されている場合に、外挿法を `"biharmonic"` に設定します。	曲面近似 — `biharmonicinterp`
`"pchip"`	区分的 3 次エルミート内挿多項式 (PCHIP) 外挿。この手法は、近似データの凸包の外側に形状維持 PCHIP を拡張します。詳細については、`pchip` を参照してください。 `fit` は、`pchipinterp` 曲線近似の `ExtrapolationMethod` が `"auto"` に設定されている場合に、外挿法を `"pchip"` に設定します。	曲線近似 — `pchipinterp`
`"cubic"`	3 次スプライン外挿。この手法は、近似データの凸包の外側に 3 次内挿スプラインを拡張します。 `fit` は、`cubicinterp` 曲線近似および `cubicspline` 曲線近似の `ExtrapolationMethod` が `"auto"` に設定されている場合に、外挿法を `"cubic"` に設定します。詳細については、`spline` を参照してください。	曲線近似 — `cubicinterp` 、`cubicspline`

データ型: char | string

線形および非線形最小二乗法のオプション

`Robust` — ロバスト線形最小二乗近似法
`'off'` (既定値) | `LAR` | `Bisquare`

ロバスト線形最小二乗近似法。'Robust' と次のいずれかの値で構成されるコンマ区切りのペアとして指定します。

'LAR' — 最小絶対残差法を指定する。
'Bisquare' — 二重平方重み法を指定する。

近似タイプ Method が LinearLeastSquares または NonlinearLeastSquares のときに使用できます。

データ型: char

`Lower` — 近似される係数の下限
[ ] (既定値) | ベクトル

近似される係数の下限。'Lower' とベクトルで構成されるコンマ区切りのペアとして指定します。既定値は空のベクトルであり、近似が下限によって制約されないことを示します。範囲を指定する場合、ベクトルの長さは係数の数と等しくなければなりません。ベクトル値の係数のエントリ順序を確認するには、関数 coeffnames を使用します。例については、開始点と範囲を設定するための係数順序の確認を参照してください。個々の制約なしの下限は -Inf によって指定できます。

Method が LinearLeastSquares または NonlinearLeastSquares のときに使用できます。

データ型: double

`Upper` — 近似される係数の上限
[ ] (既定値) | ベクトル

近似される係数の上限。'Upper' とベクトルで構成されるコンマ区切りのペアとして指定します。既定値は空のベクトルであり、近似が上限によって制約されないことを示します。範囲を指定する場合、ベクトルの長さは係数の数と等しくなければなりません。ベクトル値の係数のエントリ順序を確認するには、関数 coeffnames を使用します。例については、開始点と範囲を設定するための係数順序の確認を参照してください。個々の制約なしの上限は +Inf によって指定できます。

Method が LinearLeastSquares または NonlinearLeastSquares のときに使用できます。

データ型: logical

非線形最小二乗法のオプション