このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

fittype

曲線近似および曲面近似の近似タイプ

構文

aFittype = fittype(libraryModelName)

aFittype = fittype(expression)

aFittype = fittype(expression,Name,Value)

aFittype = fittype(linearModelTerms)

aFittype = fittype(linearModelTerms,Name,Value)

aFittype = fittype(anonymousFunction)

aFittype = fittype(anonymousFunction,Name,Value)

説明

aFittype = fittype(libraryModelName) は、libraryModelName で指定されたモデルの fittype オブジェクト aFittype を作成します。

aFittype = fittype(expression) は MATLAB^® 式で指定されたモデルの近似タイプを作成します。

aFittype = fittype(expression,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して近似タイプを構成します。

aFittype = fittype(linearModelTerms) は、linearModelTerms の式で指定された項を使用してカスタム線形モデルの近似タイプを作成します。

aFittype = fittype(linearModelTerms,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して近似タイプを構成します。

aFittype = fittype(anonymousFunction) は anonymousFunction で指定されたモデルの近似タイプを作成します。

aFittype = fittype(anonymousFunction,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して近似タイプを構成します。

例

ライブラリ モデルの近似タイプの作成

ライブラリ モデル名を指定して近似タイプを構成します。

3 次多項式ライブラリ モデルの fittype オブジェクトを構成します。

f = fittype('poly3')

f = 
     Linear model Poly3:
     f(p1,p2,p3,p4,x) = p1*x^3 + p2*x^2 + p3*x + p4

ライブラリ モデル rat33 (分子と分母の両方が 3 次の有理モデル) の近似タイプを構成します。

f = fittype('rat33')

f = 
     General model Rat33:
     f(p1,p2,p3,p4,q1,q2,q3,x) = (p1*x^3 + p2*x^2 + p3*x + p4) /
               (x^3 + q1*x^2 + q2*x + q3)

ライブラリ モデル名の一覧については、libraryModelName を参照してください。

カスタム非線形モデルの作成と、問題のパラメーターおよび独立変数の指定

問題依存のパラメーターと独立変数を指定して、カスタム非線形モデルの近似タイプを構成します。

n を問題依存のパラメーター、u を独立変数に指定して、カスタム非線形モデルの近似タイプを構成します。

g = fittype('a*u+b*exp(n*u)',...
            'problem','n',...
            'independent','u')

g = 
     General model:
     g(a,b,n,u) = a*u+b*exp(n*u)

time を独立変数に指定して、カスタム非線形モデルの近似タイプを構成します。

g = fittype('a*time^2+b*time+c','independent','time','dependent','height')

g = 
     General model:
     g(a,b,c,time) = a*time^2+b*time+c

あるデータの対数近似の近似タイプを構成します。その近似タイプを使用して近似を作成し、プロットします。

x = linspace(1,100);  
y = 5 + 7*log(x);
myfittype = fittype('a + b*log(x)',...
    'dependent',{'y'},'independent',{'x'},...
    'coefficients',{'a','b'})

myfittype = 
     General model:
     myfittype(a,b,x) = a + b*log(x)

myfit = fit(x',y',myfittype)

Warning: Start point not provided, choosing random start point.

myfit = 
     General model:
     myfit(x) = a + b*log(x)
     Coefficients (with 95% confidence bounds):
       a =           5  (5, 5)
       b =           7  (7, 7)

plot(myfit,x,y)

任意の MATLAB コマンドを指定できます。そのため、任意の .m ファイルを指定できます。

カスタム線形モデルの作成

線形近似アルゴリズムを使用するには、項の cell 配列を指定します。

fittype に入力する必要がある線形モデル a*x + b*sin(x) + c の項を特定します。このモデルは a、b、c について線形です。これには 3 つの項 x、sin(x)、1 (c=c*1 であるため) があります。このモデルを指定するには、項の cell 配列 LinearModelTerms = {'x','sin(x)','1'} を使用します。

線形モデルの項の cell 配列を fittype への入力として使用します。

ft = fittype({'x','sin(x)','1'})

ft = 
     Linear model:
     ft(a,b,c,x) = a*x + b*sin(x) + c

a*cos(x) + b の線形モデル近似タイプを作成します。

ft2 = fittype({'cos(x)','1'})

ft2 = 
     Linear model:
     ft2(a,b,x) = a*cos(x) + b

再度近似タイプを作成し、係数名を指定します。

ft3 = fittype({'cos(x)','1'},'coefficients',{'a1','a2'})

ft3 = 
     Linear model:
     ft3(a1,a2,x) = a1*cos(x) + a2

ファイルで定義された曲線による近似

ファイルに関数を定義し、それを使用して近似タイプを作成し曲線で近似します。

関数を MATLAB ファイルに定義します。

function y = piecewiseLine(x,a,b,c,d,k)
% PIECEWISELINE   A line made of two pieces
% that is not continuous.

y = zeros(size(x));

% This example includes a for-loop and if statement
% purely for example purposes.
for i = 1:length(x)
    if x(i) < k,
        y(i) = a + b.* x(i);
    else
        y(i) = c + d.* x(i);
    end
end
end

ファイルを保存します。

データを定義し、関数 piecewiseLine を指定して近似タイプを作成します。その近似タイプ ft を使用して近似を作成し、結果をプロットします。

x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;...
    0.96;0.96;0.16;0.97;0.96];
y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;...
    0.15;-0.046;0.17;-0.091;-0.071];
ft = fittype( 'piecewiseLine( x, a, b, c, d, k )' )
f = fit( x, y, ft, 'StartPoint', [1, 0, 1, 0, 0.5] )
plot( f, x, y )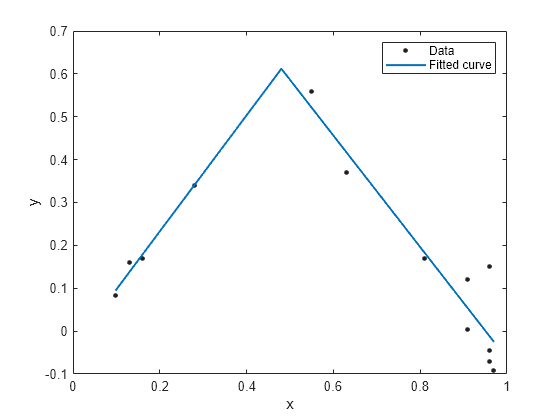 

無名関数を使用した近似タイプの作成

無名関数を使用して近似タイプを作成します。

g = fittype( @(a, b, c, x) a*x.^2+b*x+c )

無名関数を使用して近似タイプを作成し、独立パラメーターと従属パラメーターを指定します。

g = fittype( @(a, b, c, d, x, y) a*x.^2+b*x+c*exp(...
 -(y-d).^2 ), 'independent', {'x', 'y'},...
     'dependent', 'z' );

無名関数を使用して曲面の近似タイプを作成し、独立パラメーター、従属パラメーター、fit を呼び出すときに後で指定する問題のパラメーターを指定します。

g = fittype( @(a,b,c,d,x,y) a*x.^2+b*x+c*exp( -(y-d).^2 ), ...
        'problem', {'c','d'}, 'independent', {'x', 'y'}, ...
        'dependent', 'z' ); 

無名関数を使用した、近似へのワークスペース データの受け渡し

無名関数を使用して、ワークスペース データを関数 fittype および fit に渡します。

S 字型の曲線を作成しプロットします。後の手順で、この曲線の引き伸ばしと移動を行いデータを近似します。

% Breakpoints.
xs = (0:0.1:1).';
% Height of curve at breakpoints.
ys = [0; 0; 0.04; 0.1; 0.2; 0.5; 0.8; 0.9; 0.96; 1; 1];
% Plot S-shaped curve.
xi = linspace( 0, 1, 241 );
plot( xi, interp1( xs, ys, xi, 'pchip' ), 'LineWidth', 2 )
hold on
plot( xs, ys, 'o', 'MarkerFaceColor', 'r' )
hold off
title S-curve

無名関数を使用して近似タイプを作成します。このとき、曲線のブレークポイント (xs) とブレークポイントでの曲線の高さ (ys) の値をワークスペースから取得します。係数は b (ベース) と h (高さ) です。

ft = fittype( @(b, h, x) interp1( xs, b+h*ys, x, 'pchip' ) )

係数の例としてベース b=1.1 と高さ h=-0.8 を指定して、fittype をプロットします。

plot( xi, ft( 1.1, -0.8, xi ), 'LineWidth', 2 )
title 'Fittype with b=1.1 and h=-0.8'

データを読み込み、ワークスペースの値を使用して作成した近似タイプ ft で近似します。

% Load some data
xdata = [0.012;0.054;0.13;0.16;0.31;0.34;0.47;0.53;0.53;...
   0.57;0.78;0.79;0.93];
ydata = [0.78;0.87;1;1.1;0.96;0.88;0.56;0.5;0.5;0.5;0.63;...
   0.62;0.39];
% Fit the curve to the data
f = fit( xdata, ydata, ft, 'Start', [0, 1] )
% Plot fit
plot( f, xdata, ydata )
title 'Fitted S-curve'

無名関数を使用した、問題のパラメーターとワークスペース変数の操作

この例では、無名関数で問題のパラメーターを使用する場合とワークスペース変数の値を使用する場合の違いを示します。

データを読み込み、問題のパラメーターを指定した無名関数を使用して曲線の近似タイプを作成し、問題のパラメーターを指定して fit を呼び出します。

% Load some data.
xdata = [0.098;0.13;0.16;0.28;0.55;0.63;0.81;0.91;0.91;...
    0.96;0.96;0.96;0.97];
ydata = [0.52;0.53;0.53;0.48;0.33;0.36;0.39;0.28;0.28;...
    0.21;0.21;0.21;0.2];

% Create a fittype that has a problem parameter.
g = fittype( @(a,b,c,x) a*x.^2+b*x+c, 'problem', 'c' )

% Examine coefficients. Observe c is not a coefficient.
coeffnames( g )

% Examine arguments. Observe that c is an argument.
argnames( g )

% Call fit and specify the value of c.
f1 = fit( xdata, ydata, g, 'problem', 0, 'StartPoint', [1, 2] )

% Note: Specify start points in the calls to fit to
% avoid warning messages about random start points
% and to ensure repeatability of results.

% Call fit again and specify a different value of c,
% to get a new fit.
f2 = fit( xdata, ydata, g, 'problem', 1, 'start', [1, 2] )

% Plot results. Observe the specified c constants
% do not make a good fit.
plot( f1, xdata, ydata )
hold on
plot( f2, 'b' )
hold off

前の例を変更し、問題のパラメーターを使用する代わりに、変数のワークスペース値を使用して同じ近似を作成します。同じデータを使用し、変数 c のワークスペース値を指定した無名関数を使用して曲線の近似タイプを作成します。

% Remove c from the argument list.
try
    g = fittype( @(a,b,x) a*x.^2+b*x+c )
catch e
    disp( e.message )
end
% Observe error because now c is undefined.
% Define c and create fittype:
c = 0;
g1 = fittype( @(a,b,x) a*x.^2+b*x+c )

% Call fit (now no need to specify problem parameter).
f1 = fit( xdata, ydata, g1, 'StartPoint', [1, 2] )
% Note that this f1 is the same as the f1 above.
% To change the value of c, recreate the fittype.
c = 1;
g2 = fittype( @(a,b,x) a*x.^2+b*x+c ) % uses c = 1
f2 = fit( xdata, ydata, g2, 'StartPoint', [1, 2] )
% Note that this f2 is the same as the f2 above.
% Plot results
plot( f1, xdata, ydata )
hold on
plot( f2, 'b' )
hold off

入力引数

libraryModelName — 近似に使用するライブラリ モデル

文字ベクトル | string スカラー

近似に使用するライブラリ モデル。文字ベクトルまたは string スカラーとして指定します。次の表にいくつかの一般的な例を示します。

ライブラリ モデル名	説明
'poly1'	線形多項式曲線
'poly11'	線形多項式曲面
'poly2'	2 次多項式曲線
'linearinterp'	区分的線形内挿
'cubicinterp'	区分的 3 次内挿
'smoothingspline'	平滑化スプライン (曲線)
'lowess'	局所線形回帰 (曲面)

ライブラリ モデル名の一覧については、モデルの名前と方程式を参照してください。

例: 'poly2'

データ型: char | string

expression — 近似に使用するモデル

文字ベクトル | string スカラー

近似に使用するモデル。文字ベクトルまたは string スカラーとして指定します。任意の MATLAB コマンドを指定できます。そのため、任意の .m ファイルを指定できます。詳細は、ファイルで定義された曲線による近似を参照してください。

データ型: char | string

linearModelTerms — 近似に使用するモデル

文字ベクトルの cell 配列 | string 配列

近似に使用するモデル。文字ベクトルの cell 配列または string 配列として指定します。文字ベクトルまたは string スカラー内の式によってモデル項を指定します。項の式には係数を含めないでください。詳細は、線形モデル項を参照してください。

データ型: cell

anonymousFunction — 近似に使用するモデル

無名関数

近似に使用するモデル。無名関数として指定します。詳細は、無名関数の入力順序を参照してください。

データ型: char

名前と値の引数

引数の任意のペアを Name1=Value1,...,NameN=ValueN のように指定します。Name は引数名、Value は対応する値です。名前と値の引数は、他の引数より後に指定されている必要があります。ただし、各ペアの順序は任意です。

R2021a 以前では、それぞれの名前と値をコンマで区切り、Name を引用符で囲みます。

例: 'coefficients',{'a1','a2'}

coefficients — 係数名

文字ベクトル | string スカラー | 文字ベクトルの cell 配列 | string 配列

係数名。'coefficients' と、1 つの文字ベクトル、string スカラー、文字ベクトルの cell 配列、または string 配列で構成されるコンマ区切りのペアとして指定します。複数の文字から成る記号名を使用できます。i、j、pi、inf、nan、eps を名前として使用することはできません。

データ型: char | string | cell

dependent — 従属 (応答) 変数名

y (既定値) | 文字ベクトル | string スカラー

従属 (応答) 変数名。'dependent' と、文字ベクトルまたは string スカラーで構成されるコンマ区切りのペアとして指定します。従属変数を指定しない場合、この関数は y を従属変数と仮定します。

データ型: char | string

independent — 独立 (応答) 変数名

x (既定値) | 文字ベクトル | string スカラー | 文字ベクトルの cell 配列 | string 配列

独立 (応答) 変数名。'independent' と、1 つの文字ベクトル、string スカラー、文字ベクトルの cell 配列、または string 配列で構成されるコンマ区切りのペアとして指定します。独立変数を指定しない場合、この関数は x を独立変数と仮定します。

データ型: char | string | cell

options — 近似オプション

fitoptions

近似オプション。'options' と fitoptions オブジェクトの名前で構成されるコンマ区切りのペアとして指定します。

problem — 問題依存の (固定) パラメーター名

文字ベクトル | string スカラー | cell 配列または文字ベクトル | string 配列

問題依存の (固定) パラメーター名。'problem' と、1 つの文字ベクトル、string スカラー、文字ベクトルの cell 配列、または問題依存の定数ごとに 1 つの要素をもつ string 配列で構成されるコンマ区切りのペアとして指定します。

データ型: char | string | cell

出力引数

aFittype — 近似に使用するモデル

fittype オブジェクト

近似に使用するモデル。fittype として返されます。fittype はモデルを記述する情報をカプセル化します。近似を作成するには、データ、fittype、さらに (オプションで) fitoptions や排除規則が必要です。fittype を関数 fit への入力として使用することができます。

詳細

従属変数と独立変数

変数が従属変数であるか独立変数であるかを判断するにはどうするとよいでしょうか。

従属変数、独立変数、係数を決定するために、次の方程式を考えます。

$$y=f(x)=a+(b*x)+(c*x^2)$$.

• y は従属変数です。

• x は独立変数です。

• a、b および c は係数です。

'independent' 変数は制御対象です。'dependent' 変数は測定対象であり、独立変数に依存します。'coefficients' は近似アルゴリズムで推定するパラメーターです。

たとえば、国勢調査データの場合、年は他の値に依存しないため独立変数です。人口は、値が国勢調査の実施年に依存するため従属変数です。増加率などのパラメーターがモデルに含まれる場合、近似アルゴリズムで推定されるため、このパラメーターは 'coefficients' の 1 つです。

関数 fittype は、近似タイプの式の入力から変数名を検索して入力引数を決定します。fittype は、x が独立変数、y が従属変数、他のすべての変数がモデルの係数であると仮定します。変数が存在しない場合は、x が使用されます。

無名関数の入力順序

近似タイプの式の入力が無名関数である場合、入力の順序が正しくなければなりません。この入力の順序に基づいて、関数 fittype はどの入力が推定する係数、問題依存のパラメーター、独立変数であるかを判断します。

無名関数の入力引数の順序は次のとおりでなければなりません。

fcn = @(coefficients,problemparameters,x,y) expression

係数は少なくとも 1 つ必要です。問題のパラメーターと y はオプションです。最後の引数である x と y は独立変数を表します。曲線の場合は x のみですが、曲面の場合は x と y が必要です。x または y 以外を独立変数の名前に使用するには、'independent' 引数の名前と値のペアを使用して別の名前を指定します。ただし、どのような名前を選択する場合でも、これらの引数は無名関数の最後の引数でなければなりません。

無名関数を使用すると、他のデータを関数 fittype や fit に簡単に渡せます。

1. 無名関数とワークスペースの変数値 (c) を使用して近似タイプを作成します。

   c = 1;
    g = fittype( @(a, b, x) a*x.^2+b*x+c )

2. 近似タイプを作成するとき、関数 fittype でワークスペースの変数値を使用できます。ワークスペースから新しいデータを渡すには、次のように近似タイプを再作成します。

   c = 5 % Change value of c.
   g = fittype( @(a, b, x) a*x.^2+b*x+c )
   

3. ここで、近似タイプを作成するとき c の値は固定されます。fit を呼び出すときに c の値を指定するために、問題のパラメーターを使用することができます。たとえば、c = 2 を指定して近似を作成し、さらに c = 3 を指定して新しい近似を作成することができます。

   g = fittype( @(a,b,x,c) a*x.^2+b*x+c, 'problem', 'c' )
   f1 = fit( xdata, ydata, g, 'problem', 2 )
   f2 = fit( xdata, ydata, g, 'problem', 3 ) 

線形モデル項

線形モデル項はどのように定義するとよいでしょうか。

線形近似アルゴリズムを使用するには、linearModelTerms を項の cell 配列または string 配列として指定します。以下に例を示します。

afittype = fittype({expr1,...,exprn})

文字ベクトル expr2,...,exprn 内の式によってモデル項を指定します。項の式には係数を含めないでください。定数項がある場合は、cell 配列内で対応する式として '1' を使用します。

次の形式の線形モデルを指定する方法は次のとおりです。

 coeff1 * term1 + coeff2 * term2 + coeff3 * term3 + ...

ここで、term1、term2 などはいずれも係数を含みません。cell 配列または string 配列を使用し、expr の cell または要素として各項を係数を含めずに次のように指定します。

LinearModelTerms = {'term1', 'term2', 'term3', ... }

たとえば、次のモデルを考えます。

a*x + b*sin(x) + c

これは a、b および c について線形です。これには 3 つの項 x、sin(x)、1 (c=c*1 であるため) があります。したがって、expr は次のようになります。

LinearModelTerms = {'x','sin(x)','1'}

曲線フィッター アプリで、[近似タイプ] セクションの [カスタム] グループから [線形近似] 近似を選択します。

アルゴリズム

近似タイプの式の入力が文字ベクトル、string スカラー、または無名関数の場合、ツールボックスではモデルをデータに当てはめるために非線形近似アルゴリズムが使用されます。

近似タイプの式の入力が項の cell 配列または string 配列の場合、ツールボックスではモデルをデータに当てはめるために線形近似アルゴリズムが使用されます。

バージョン履歴

R2006a より前に導入

参考

関数

• fit | fitoptions

アプリ

• 曲線フィッター

トピック

• カスタム線形近似
• パラメトリック近似

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい