カスタム線形近似

カスタム線形モデルについて

曲線フィッターアプリで、[カスタム式] 近似を使用して独自の線形方程式または非線形方程式を定義できます。カスタム式近似では非線形最小二乗近似の手順を使用します。

[カスタム式] でカスタム線形方程式を定義できます。ただし、非線形近似は線形最小二乗近似よりも効率が悪く、通常は時間がかかります。カスタム式の線形最小二乗近似が必要な場合は、代わりに [線形近似] を選択します。線形モデルは (おそらく非線形な) 項の線形結合です。これらはパラメーターについて線形である方程式で定義されます。

ヒント

カスタム式の線形最小二乗近似が必要な場合は、[線形近似] を選択します。方程式を一連の線形関数で表せるかわからない場合は、代わりに [カスタム式] を選択します。詳細は、カスタム式近似の対話的な選択を参照してください。

線形近似によるカスタム近似の対話的な選択

曲線フィッターアプリで、曲線データを選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] および [Y データ] の値を選択します。
曲線フィッターにより、既定の多項式近似が作成されます。
モデルタイプを変更します。[曲線フィッター] タブの [近似タイプ] セクションで、矢印をクリックしてギャラリーを開きます。ギャラリーで、[カスタム] グループの [線形近似] をクリックします。
[近似オプション] ペインで [線形近似] をクリックすると式の例が表示されます。
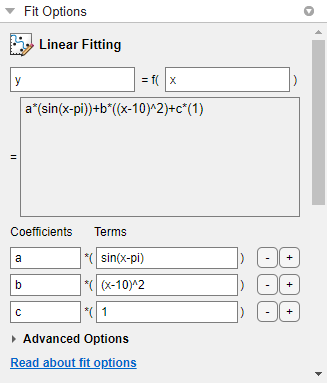
x および y を有効な任意の変数名に変更できます。
下のボックスに式の例が表示されます。[係数] および [項] のエントリを変更することで、項の例を変更して独自の式を定義します。

例については、曲線フィッターアプリでのカスタム線形ルジャンドル多項式による近似を参照してください。

コマンドラインでの線形近似の選択

線形近似アルゴリズムを使用するには、モデル項の cell 配列または string 配列を関数 fit または fittype への入力として指定します。項の式には係数を含めないでください。定数項がある場合は、配列内で対応する式として '1' を使用します。

次の形式の線形モデルを指定する方法は次のとおりです。

 coeff1 * term1 + coeff2 * term2 + coeff3 * term3 + ...

ここで、term1、term2 などはいずれも係数を含みません。cell 配列または string 配列を使用し、個別の要素として各項を係数を含めずに次のように指定します。以下に例を示します。

LinearModelTerms = {'term1', 'term2', 'term3', ... }

fittype に入力する必要がある線形モデルの項を特定します。たとえば、次のモデルを考えます。
```
a*log(x) + b*x + c
```
これは a、b および c について線形です。これには 3 つの項 log(x)、x、1 (c=c*1 であるため) があります。このモデルを指定するには、次のような項 LinearModelTerms = {'log(x)','x','1'} を使用します。

線形モデルの項の cell 配列または string 配列を関数 fittype への入力として使用します。

linearfittype = fittype({'log(x)','x','1'})

linearfittype = 

     Linear model:
     linearfittype(a,b,c,x) = a*log(x) + b*x + c

データを読み込み、fittype を関数 fit への入力として使用します。

load census
f = fit(cdate,pop,linearfittype)

f = 

     Linear model:
     f(x) = a*log(x) + b*x + c
     Coefficients (with 95% confidence bounds):
       a =  -4.663e+04  (-4.973e+04, -4.352e+04)
       b =        25.9  (24.26, 27.55)
       c =   3.029e+05  (2.826e+05, 3.232e+05)

または、線形モデルの項の cell 配列または string 配列を関数 fit への入力として指定することもできます。

f = fit(x,z,{'log(x)','x','1'})

近似とデータをプロットします。
```
plot(f,cdate,pop)
```

例については、コマンドラインでのカスタム線形ルジャンドル多項式による近似を参照してください。

カスタム線形ルジャンドル多項式による近似

曲線フィッターアプリでのカスタム線形ルジャンドル多項式による近似

この例では、いくつかのカスタム線形方程式を使用してデータに当てはめる方法を示します。データは生成済みで、核反応 ¹²C(e,e'α)⁸Be に基づいています。方程式はルジャンドル多項式の項の和を使用します。

124 MeV の電子が ¹²C の原子核から散乱する実験を考えます。これに続く反応で、アルファ粒子が放出されて残留核 ⁸Be が生成されます。放出されるアルファ粒子の数を角度の関数として解析することにより、¹²C の原子核ダイナミクスに関する特定の情報を推測できます。反応運動を次に示します。

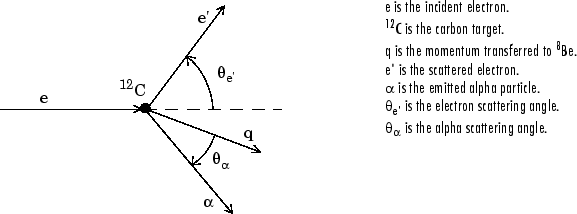
データは、半導体検出器を配置して Θ_α の値が 10^o から 240^o の範囲で 10^o 刻みで収集しています。

ルジャンドル多項式の変数を角度の関数で表すと便利な場合があります。

$y (x) = \sum_{n = 0}^{\infty} a_{n} P_{n} (x)$

ここで、P_n(x) は n 次のルジャンドル多項式、x は cos(Θ_α)、a_n は近似の係数です。ルジャンドル多項式の導出の詳細については、関数 legendre を参照してください。

アルファ線放出データの場合、理論モデルを使用して係数と原子核ダイナミクスを直接関連付けることができます。さらに、理論モデルから、上に示した無限和についての制約が導かれます。特に、反応の角運動量を考慮すると、データは偶数項のみの 4 次ルジャンドル多項式で効果的に記述されます。

ルジャンドル多項式は次のロドリゲスの公式を使用して導出できます。

$P_{n} (x) = \frac{1}{2^{n} n!} {(\frac{d}{d x})}^{n} {(x^{2} - 1)}^{n}$

4 次までのルジャンドル多項式

n	P_n(x)
0	1
1	x
2	(1/2)(3x²– 1)
3	(1/2)(5x³ – 3x)
4	(1/8)(35x⁴ – 30x² + 3)

この例では、偶数項のみの 4 次ルジャンドル多項式を使用してデータに当てはめる方法を示します。

$y_{1} (x) = a_{0} + a_{2} (\frac{1}{2}) (3 x^{2} - 1) + a_{4} (\frac{1}{8}) (35 x^{4} - 30 x^{2} + 3)$

¹²C のアルファ線放出データを読み込みます。
```
load carbon12alpha
```
このとき、ワークスペースには 2 つの新しい変数が含まれています。
- angle は角度のベクトル (ラジアン単位) であり、10^o から 240^o の範囲を 10^o 刻みで変化します。
- counts は、angle の放出角度に対応する生のアルファ粒子数のベクトルです。
曲線フィッターアプリを開きます。
```
curveFitter
```
曲線フィッターアプリ内の [曲線フィッター] タブで、[データ] セクションの [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] および [Y データ] として、それぞれ angle および counts を選択し、これらの 2 つの変数について既定の多項式近似を作成します。
近似タイプを既定のカスタム線形近似に変更します。[曲線フィッター] タブの [近似タイプ] セクションで、矢印をクリックしてギャラリーを開きます。ギャラリーで、[カスタム] グループの [線形近似] をクリックします。
[カスタム式] 近似タイプの代わりに [線形近似] を使用します。これは、ルジャンドル多項式が予測子変数と定数のみに依存するためです。このモデルに指定する方程式は y₁(x) (つまり、この手順の最初に示した方程式) です。angle はラジアン単位で与えられるため、ルジャンドル項の引数は cos(Θ_α) となります。
[近似オプション] ペインで、式の項を変更します。
1. [係数] の名前を a2、a4 および a0 に変更します。
2. a2 について、[項] の値を次のように変更します。
  (1/2)*(3*cos(x)^2-1)
  項を編集すると、曲線フィッターアプリにより近似が更新されます。
3. a4 について、[項] の値を次のように変更します。
  (1/8)*(35*cos(x)^4-30*cos(x)^2+3)
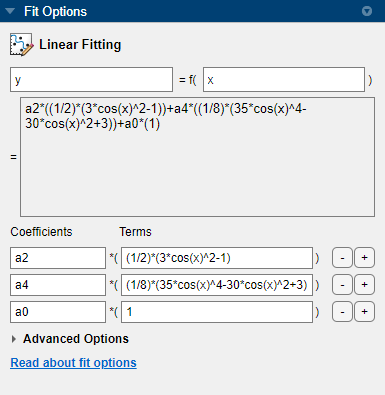
  曲線フィッターアプリに近似が表示されます。
[近似テーブル] ペインで、[近似名] の値をダブルクリックして Leg4Even に変更します。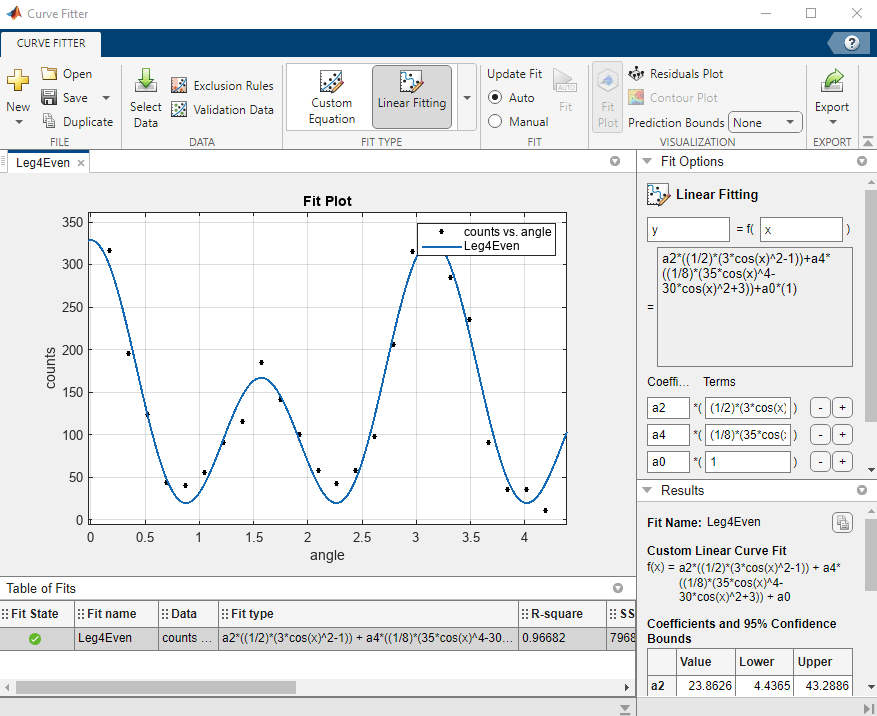
残差を表示します。[曲線フィッター] タブの [可視化] セクションで [残差プロット] をクリックします。
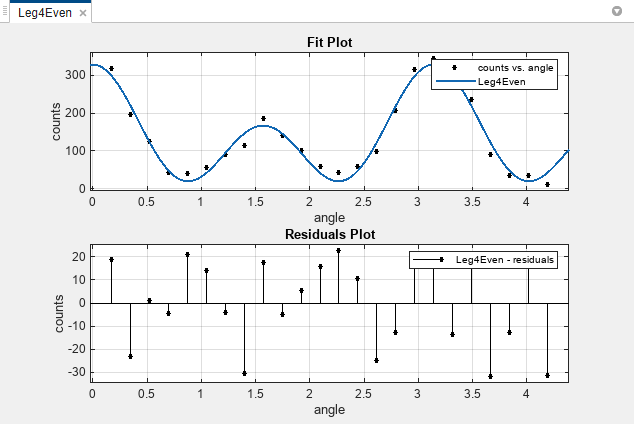
この近似はデータトレンドにうまく従っているように見えます。一方、残差は一見ランダムに分布しており、体系的な振る舞いは見られません。
[結果] ペインで数値的な近似結果を検証します。各係数値とかっこ内の信頼限界を確認します。95% 信頼限界は、a₀(x) および a₄(x) に関連する係数はかなり正確に求められたが、係数 a₂(x) は比較的大きな不確定性をもつことを示しています。
アルファ線放出データは偶数項のみの 4 次ルジャンドル多項式によって最も適切に記述されるという理論的議論を確認するために、次に偶数項と奇数項の両方を使用してデータに当てはめます。
$y_{2} (x) = y_{1} (x) + a_{1} x + a_{3} (\frac{1}{2}) (5 x^{3} - 3 x)$
まず、変更するルジャンドル多項式のコピーを作成します。[曲線フィッター] タブの [ファイル] セクションで [複製] をクリックします。複製された近似が [近似] ペインの新しいタブに表示されます。
[近似テーブル] ペインで、新しい近似の名前を Leg4EvenOdd に変更します。
[近似オプション] ペインで、式の項を変更します。
次のように項を編集し、y₂(x) で与えられるモデルにより近似します。
1. 最後の [+] ボタンを 2 回クリックして、奇数次のルジャンドル項を追加します。
2. 新しい係数名を a1 および a3 に変更します。
3. a1 について、[項] の値を次のように変更します。
  cos(x)
4. a3 について、[項] の値を次のように変更します。
  (1/2)*(5*cos(x)^3-3*cos(x))
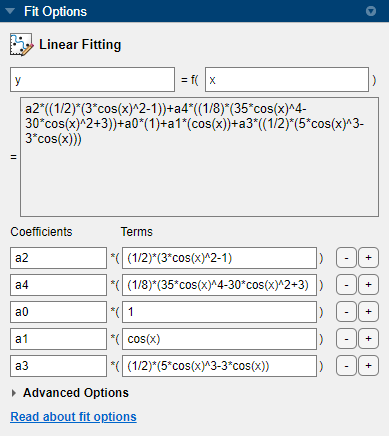
曲線フィッターアプリにプロットされた新しい近似を観察し、[結果] ペインの数値結果を調べます。
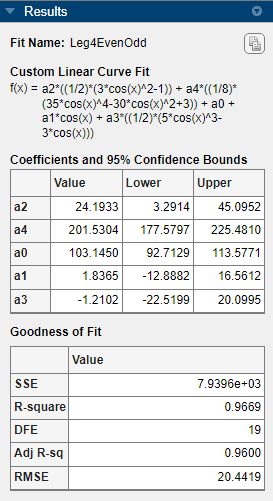
奇数項のルジャンドル係数 (a1 および a3) は、値が小さく信頼限界にゼロが含まれているため、近似を簡略化するために削除できる候補であると考えられます。この結果は、奇数次のルジャンドル項は近似にあまり寄与せず、偶数次のルジャンドル項は前の近似と基本的に変わらないことを示しています。これにより、近似 Leg4Even での最初のモデル選択が最適であることが確認されます。
近似を左右に並べて比較します。近似の Figure タブの右端にある [ドキュメントアクション] の矢印をクリックします。[すべて並べて表示] オプションを選択して、1 行 2 列のレイアウトを指定します。
[近似オプション]、[結果]、[近似テーブル] の各ペインをドラッグして非表示にし、プロットのみを表示することもできます。

コマンドラインでのカスタム線形ルジャンドル多項式による近似

曲線フィッターアプリで作成したものと同じモデルを使用してコマンドラインで当てはめます。

線形近似アルゴリズムを使用するには、モデル項の cell 配列または string 配列を関数 fittype への入力として指定します。曲線フィッターアプリで近似 Leg4Even に入力したものと同じ [項] を使用します。係数は指定しないでください。
```
linearft = fittype({'(1/2)*(3*cos(x)^2-1)', ...
'(1/8)*(35*cos(x)^4-30*cos(x)^2+3)','1'})
```
```
linearft = 

     Linear model:
     linearft(a,b,c,x) = a*((1/2)*(3*cos(x)^2-1))...
       + b*((1/8)*(35*cos(x)^4-30*cos(x)^2+3)) + c
```
変数 angle および counts をワークスペースに読み込みます。
```
load carbon12alpha
```

fittype を関数 fit への入力として使用し、ワークスペースの変数 angle および counts を指定します。

f = fit(angle,counts,linearft)

f = 

     Linear model:
     f(x) = a*((1/2)*(3*cos(x)^2-1))...
     + b*((1/8)*(35*cos(x)^4-30*cos(x)^2+3)) + c
     Coefficients (with 95% confidence bounds):
       a =       23.86  (4.436, 43.29)
       b =       201.9  (180.2, 223.6)
       c =       102.9  (93.21, 112.5)

近似とデータをプロットします。
```
plot(f,angle,counts)
```

線形モデル項の詳細については、関数 fittype を参照してください。