legendre

ルジャンドル陪関数

構文

P = legendre(n,X)

P = legendre(n,X,normalization)

説明

P = legendre(n,X) は、X の各要素に対し求められる次数 n および位数 m = 0, 1, ..., n のルジャンドル陪関数を計算します。

P = legendre(n,X,normalization) は、ルジャンドル陪関数の正規化されたバージョンを計算します。normalization は 'unnorm' (既定)、'sch'、'norm' のいずれかにできます。

例

ベクトルのルジャンドル陪関数値

関数 legendre を使用して、ベクトルに対して演算を行い、出力の形式を確認します。

ベクトルの 2 次ルジャンドル関数値を計算します。

deg = 2;
x = 0:0.1:0.2;
P = legendre(deg,x)

P = 3×3

   -0.5000   -0.4850   -0.4400
         0   -0.2985   -0.5879
    3.0000    2.9700    2.8800

出力の形式は次のようになります。

• 各行には、m (ルジャンドル陪関数の位数) の個々の値についての関数値が含まれます。

• 各列には、x の個々の値についての関数値が含まれます。

$$\begin{array}{cccc}& \text{x}\text{=}\text{0}& \text{x}\text{=}\text{0.1}& \text{x}\text{=}\text{0.2}\\ \text{m}\text{=}\text{0}& P_2^0(0)& P_2^0(0.1)& P_2^0(0.2)\\ \text{m}\text{=}\text{1}& P_2^1(0)& P_2^1(0.1)& P_2^1(0.2)\\ \text{m}\text{=}\text{2}& P_2^2(0)& P_2^2(0.1)& P_2^2(0.2)\end{array}$$

2 次ルジャンドル陪関数の方程式 ${\mathit{P}}_2^{\mathit{m}}$ は次のとおりです。

$$P_2^m(x)={(-1)}^m{(1-x^2)}^{m/2}\frac{d^m}{d{x}^m}\left[\frac{1}{2}(3x^2-1)\right].$$

そのため、${\mathit{P}}_2^0\left(0\right)$ の値は次のとおりです。

$$P_2^0(0)=\left[\frac{1}{2}(3x^2-1)\right]{|}_{x=0}=-\frac{1}{2}.$$

この結果は P(1,1) = -0.5000 と一致します。

ルジャンドル正規化の比較

複数の正規化を使用してルジャンドル陪関数を計算します。

1 次非正規化ルジャンドル関数値 ${\mathit{P}}_1^{\mathit{m}}$ を計算します。値の 1 番目の行は $\mathit{m}=0$ に対応し、2 番目の行は $\mathit{m}=1$ に対応します。

x = 0:0.2:1;
n = 1;
P_unnorm = legendre(n,x)

P_unnorm = 2×6

         0    0.2000    0.4000    0.6000    0.8000    1.0000
   -1.0000   -0.9798   -0.9165   -0.8000   -0.6000         0

次に、シュミット半正規化関数値を計算します。$\mathit{m}>0$ の場合に、非正規化値と比べて、シュミット型は次のスケーリングの分だけ異なります。

$${(-1)}^m\sqrt{\frac{2(n-m)!}{(n+m)!}}.$$

1 行目では、$\mathit{m}=0$ であるため、2 つの正規化は同じです。2 行目では、各値に乗算されるスケーリング定数は -1 です。

P_sch = legendre(n,x,'sch')

P_sch = 2×6

         0    0.2000    0.4000    0.6000    0.8000    1.0000
    1.0000    0.9798    0.9165    0.8000    0.6000         0

C1 = (-1) * sqrt(2*factorial(0)/factorial(2))

C1 = 
-1

最後に、完全に正規化された関数値を計算します。非正規化値と比べて、完全に正規化された形式は、次のスケーリング ファクターの分だけ異なります。

$${(-1)}^m\sqrt{\frac{(n+\frac{1}{2})(n-m)!}{(n+m)!}}.$$

このスケーリング係数は $\mathit{m}$ のすべての値に適用されます。そのため、1 行目と 2 行目ではスケーリング係数が異なります。

P_norm = legendre(n,x,'norm')

P_norm = 2×6

         0    0.2449    0.4899    0.7348    0.9798    1.2247
    0.8660    0.8485    0.7937    0.6928    0.5196         0

Cm0 = sqrt((3/2))

Cm0 = 
1.2247

Cm1 = (-1) * sqrt((3/2)/2)

Cm1 = 
-0.8660

球面調和関数の計算

球面調和関数はラプラス方程式の解の中に現れ、球の表面で定義される関数を表すために使用されます。${\mathit{Y}}_3^2$ の球面調和関数を計算および表示するには、legendre を使用します。

球面調和関数の方程式には、ルジャンドル関数の項と、複素指数が含まれます。

$$Y_l^m(\theta ,\varphi )=\sqrt{\frac{(2l+1)(l-m)!}{4\pi (l+m)!}}{P}_l^m(\cos \theta )e^{im\varphi },-l\le m\le l.$$

最初に、$0\le \theta \le \pi$ (余緯度角) と $0\le \varphi \le 2\pi$ (方位角) のすべての組み合わせを表す値のグリッドを作成します。ここで、余緯度 $$\theta$$ の範囲は 0 (北極) から $$\pi /2$$ (赤道) まで、および $$\pi$$ (南極) までです。

dx = pi/60;
col = 0:dx:pi;
az = 0:dx:2*pi;
[phi,theta] = meshgrid(az,col);

$\mathit{l}=3$ について、グリッド上で ${\mathit{P}}_{\mathit{l}}^{\mathit{m}}\left(\cos \theta \right)$ を計算します。

l = 3;
Plm = legendre(l,cos(theta));

legendre は $\mathit{m}$ のすべての値についての解を計算するため、Plm には余分な関数値も含まれます。$\mathit{m}=2$ についての値を抽出し、残りを破棄します。関数 reshape を使用して、結果の向きを phi および theta と同じサイズの行列とします。

m = 2;
if l ~= 0
    Plm = reshape(Plm(m+1,:,:),size(phi));
end

${\mathit{Y}}_3^2$ の球面調和関数値を計算します。

a = (2*l+1)*factorial(l-m);
b = 4*pi*factorial(l+m);
C = sqrt(a/b);
Ylm = C .*Plm .*exp(1i*m*phi);

球面座標を直交座標に変換します。ここで、$$\pi /2-\theta$$ は、$$\pi /2$$ (北極) から 0 (赤道) まで、および $$-\pi /2$$ (南極) までの範囲の緯度角になります。正と負の両方の実数値を使用して ${\mathit{Y}}_3^2$ の球面調和関数をプロットします。

[Xm,Ym,Zm] = sph2cart(phi, pi/2-theta, abs(real(Ylm)));
surf(Xm,Ym,Zm)
title('$Y_3^2$ spherical harmonic','interpreter','latex')

入力引数

n — ルジャンドル関数の次数

正の整数

ルジャンドル関数の次数。正の整数として指定します。legendre は、指定した次数について、m = 0 から m = n までのすべての位数 m に対して $$P_n^m\left(x\right)$$ を計算します。

例: legendre(2,X)

X — 入力値

スカラー | ベクトル | 行列 | 多次元配列

入力値。スカラー、ベクトル、行列、または [-1,1] の範囲の実数値の多次元配列として指定します。たとえば、球面調和関数の場合、入力値として X = cos(theta) を使用して $$P_n^m\left(\cos \theta \right)$$ を計算することが一般的です。

例: legendre(2,cos(theta))

データ型: single | double

normalization — 正規化タイプ

'unnorm' (既定値) | 'sch' | 'norm'

正規化タイプ。次の値のいずれかとして指定します。

値	結果
'unnorm'	ルジャンドル陪関数
'sch'	シュミット半正規化ルジャンドル陪関数
'norm'	完全正規化ルジャンドル陪関数

例: legendre(n,X,'sch')

出力引数

P — ルジャンドル陪関数値

スカラー | ベクトル | 行列 | 多次元配列

ルジャンドル陪関数値。スカラー、ベクトル、行列または多次元配列として返されます。P の正規化は、normalization の値に依存します。

P のサイズは X のサイズによって異なります。

• X がベクトルの場合、P はサイズが (n+1) 行 length(X) 列の行列です。P(m+1,i) 要素は、X(i) で求められる次数 n、位数 m のルジャンドル陪関数の値です。

• 一般に、P は X より 1 次元高く、各要素 P(m+1,i,j,k,...) には、X(i,j,k,...) で求められる次数 n、位数 m のルジャンドル陪関数が含まれます。

制限

非正規化ルジャンドル陪関数の値は、n > 150 の場合は倍精度数の範囲からオーバーフローし、n > 28 の場合は単精度数の範囲からオーバーフローします。このオーバーフローにより、Inf 値と NaN 値が発生します。これらのしきい値より大きい位数については、代わりに 'sch' または 'norm' 正規化を使用するようにしてください。

詳細

ルジャンドル陪関数

ルジャンドル陪関数 $$y=P_n^m\left(x\right)$$ は、次の一般ルジャンドル微分方程式の解です。

$$\left(1-x^2\right)\frac{d^{2}y}{d{x}^2}-2x\frac{dy}{dx}+\left[n\left(n+1\right)-\frac{m^2}{1-x^2}\right]y=0.$$

n はルジャンドル陪関数の整数次数、m は整数位数で、$$0\le m\le n$$ が成立します。

ルジャンドル陪関数 $$P_n^m\left(x\right)$$ はこの方程式の最も一般的な解で、次のように表されます。

$$P_n^m\left(x\right)={\left(-1\right)}^m{\left(1-x^2\right)}^{m/2}\frac{d^m}{d{x}^m}{P}_n\left(x\right).$$

これはルジャンドル多項式 $$P_n\left(x\right)$$ の微分に基づいて定義されます。これは次のように表される解の一部です。

$$P_n\left(x\right)=\frac{1}{2^{n}n!}\frac{d^n}{d{x}^n}{\left(x^2-1\right)}^n.$$

最初のいくつかのルジャンドル多項式は次のとおりです。

n の値	$$P_n\left(x\right)$$
0	$$P_0\left(x\right)=1$$
1	$$P_1\left(x\right)=x$$
2	$$P_2\left(x\right)=\frac{1}{2}\left(3x^2-1\right)$$

シュミット半正規化ルジャンドル陪関数

シュミット半正規化ルジャンドル陪関数は、非正規化ルジャンドル陪関数 $$P_n^m\left(x\right)$$ と次の関係があります。

$$\begin{array}{l}{P}_n\left(x\right)\text{ for }m=0,\\ S_n^m\left(x\right)={\left(-1\right)}^m\sqrt{\frac{2\left(n-m\right)!}{\left(n+m\right)!}}{P}_n^m\left(x\right)\text{ for }m>0.\end{array}$$

完全正規化ルジャンドル陪関数

完全正規化ルジャンドル陪関数は次のように正規化され、

$${\displaystyle {\int }_{-1}^1{\left[N_n^m(x)\right]}^{2}dx}=1.$$

正規化関数は非正規化ルジャンドル陪関数 $$P_n^m\left(x\right)$$ と次の関係があります。

$$N_n^m\left(x\right)={\left(-1\right)}^m\sqrt{\frac{\left(n+\frac{1}{2}\right)\left(n-m\right)!}{\left(n+m\right)!}}{P}_n^m\left(x\right).$$

アルゴリズム

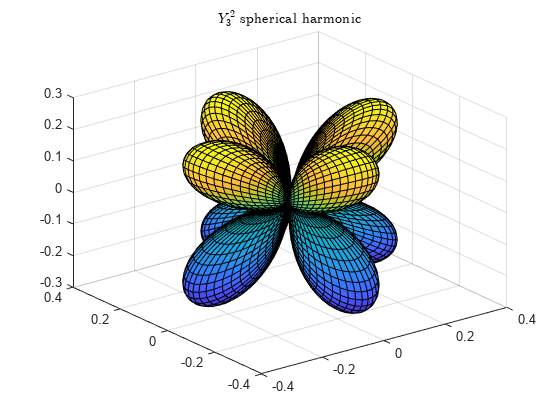
関数 legendre は m における 3 項の逆方向再帰の関係を使用します。この再帰は、複素球面調和関数であるシュミット半正規化ルジャンドル陪関数 $$Q_n^m\left(x\right)$$ の一種に関するものです。これらの関数は、次の式により標準の Abramowitz および Stegun [1]の関数 $$P_n^m\left(x\right)$$ に関連付けられています。

$$P_n^m\left(x\right)=\sqrt{\frac{\left(n+m\right)!}{\left(n-m\right)!}}{Q}_n^m\left(x\right).$$

これらは、以下によってシュミット型に関連付けられています。

$$\begin{array}{l}m=0:S_n^m\left(x\right)=Q_n^0\left(x\right)\\ m>0:S_n^m\left(x\right)={\left(-1\right)}^m\sqrt{2}{Q}_n^m\left(x\right).\end{array}$$

参照

[1] Abramowitz, M. and I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, Ch.8.

[2] Jacobs, J. A., Geomagnetism, Academic Press, 1987, Ch.4.

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

legendre 関数は、GPU 配列を完全にサポートします。GPU 上で関数を実行するには、入力データを gpuArray (Parallel Computing Toolbox) として指定します。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

beta | gamma | besselj | bessely | factorial