このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

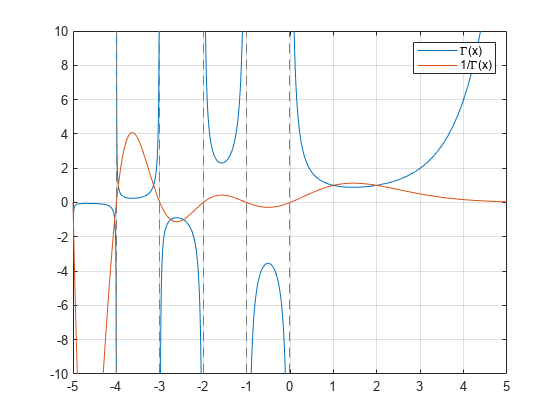
gamma

ガンマ関数

構文

Y = gamma(X)

説明

Y = gamma(X) は、X の要素で評価される関数 gamma を返します。

例

ガンマ関数の評価

スカラーおよびベクトルでガンマ関数を評価します。

$$\Gamma (0.5)$$ を評価します。これは、$$\sqrt{\pi }$$ と等しくなります。

y = gamma(0.5)

y = 1.7725

[-3.5 3.5] 内の複数の値のガンマ関数を評価します。

x = -3.5:3.5;
y = gamma(x)

y = 1×8

    0.2701   -0.9453    2.3633   -3.5449    1.7725    0.8862    1.3293    3.3234

ガンマ関数のプロット

ガンマ関数とその逆数をプロットします。

fplot を使用して、ガンマ関数とその逆数をプロットします。ガンマ関数は、正の引数では急速に増加し、すべての負の整数の引数 (および 0) で単純極をもちます。この関数はゼロになりません。一方、逆数ガンマ関数は、すべての負の整数の引数 (および 0) でゼロになります。

fplot(@gamma)
hold on
fplot(@(x) 1./gamma(x))
ylim([-10 10])
legend('\Gamma(x)','1/\Gamma(x)')
hold off
grid on

入力引数

X — 入力配列

スカラー | ベクトル | 行列 | 多次元配列

入力配列。スカラー、ベクトル、行列または多次元配列として指定します。X の要素は実数でなければなりません。

データ型: single | double

制限

• データ型が double および single の場合、関数 gamma は realmax および realmax('single') より大きなすべての値について Inf を返します。正の整数値の飽和しきい値は gamma(172) および gamma(single(36)) です。この場合、評価された関数 gamma は表現可能な最大値より大きくなります。

詳細

ガンマ関数

関数 gamma は、実数 x > 0 について次の積分式によって定義されます。

$$\Gamma (x)={\displaystyle {\int }_0^{\infty }{e}^{-t}}{t}^{x-1}dt$$

関数 gamma は、関数 factorial を内挿します。整数 n に対して、次のようになります。

gamma(n+1) = factorial(n) = prod(1:n)

関数 gamma の定義域は解析接続により負の実数に拡張され、負の整数に単純極を持ちます。この拡張は、次の再帰の関係を繰り返し適用することで得られます。

$$\Gamma \left(n-1\right)=\frac{\Gamma \left(n\right)}{n-1}.$$

アルゴリズム

gamma の計算は[1]に概説されているアルゴリズムに基づいています。

参照

[1] Cody, J., An Overview of Software Development for Special Functions, Lecture Notes in Mathematics, 506, Numerical Analysis Dundee, G. A. Watson (ed.), Springer Verlag, Berlin, 1976.

[2] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965, sec. 6.5.

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

この関数は tall 配列を完全にサポートしています。詳細については、tall 配列を参照してください。

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は GPU 配列を完全にサポートしています。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

この関数は分散配列を完全にサポートしています。詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

gammainc | gammaincinv | gammaln | psi | factorial