このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

bessely

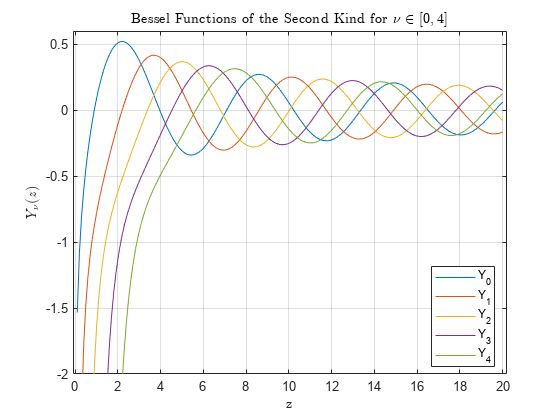
第 2 種ベッセル関数

構文

Y = bessely(nu,Z)

Y = bessely(nu,Z,scale)

説明

Y = bessely(nu,Z) は、配列 Z の各要素について第 2 種ベッセル関数 Y_ν(z) を計算します。

Y = bessely(nu,Z,scale) は、オーバーフローや精度の低下を防ぐために第 2 種変形ベッセル関数を指数的にスケーリングするかどうかを指定します。scale が 1 の場合、bessely の出力は係数 exp(-abs(imag(Z))) でスケーリングされます。

例

第 2 種ベッセル関数のプロット

領域を定義します。

z = 0:0.1:20;

最初の 5 つの第 2 種ベッセル関数を計算します。Y の各行には、z の各点で評価された関数の 1 つの次数の値が含まれます。

Y = zeros(5,201);
for i = 0:4
    Y(i+1,:) = bessely(i,z);
end

すべての関数を同じ Figure にプロットします。

plot(z,Y)
axis([-0.1 20.2 -2 0.6])
grid on
legend('Y_0','Y_1','Y_2','Y_3','Y_4','Location','Best')
title('Bessel Functions of the Second Kind for $\nu \in [0, 4]$','interpreter','latex')
xlabel('z','interpreter','latex')
ylabel('$Y_\nu(z)$','interpreter','latex')

指数的にスケーリングされたベッセル関数の計算

複素数値 $\mathit{z}$ について、第 2 種ベッセル関数 ${\mathit{Y}}_2\left(\mathit{z}\right)$ のスケーリングされていない関数 (Y) とスケーリングされた関数 (Ys) を計算します。

x = -10:0.35:10;
y = x';
z = x + 1i*y;
scale = 1;
Y = bessely(2,z);
Ys = bessely(2,z,scale);

スケーリングされた関数とスケーリングされていない関数の虚数部のプロットを比較します。abs(imag(z)) の値が大きい場合、スケーリングされていない関数は倍精度の範囲からすぐにオーバーフローし、計算できなくなります。スケーリングされた関数では、この支配的な指数的挙動が計算から除外されるため、スケーリングされていない関数と比べて計算可能な範囲が大きくなります。

surf(x,y,imag(Y))
title('Bessel Function of the Second Kind','interpreter','latex')
xlabel('real(z)','interpreter','latex')
ylabel('imag(z)','interpreter','latex')

surf(x,y,imag(Ys))
title('Scaled Bessel Function of the Second Kind','interpreter','latex')
xlabel('real(z)','interpreter','latex')
ylabel('imag(z)','interpreter','latex')

入力引数

nu — 方程式の次数

スカラー | ベクトル | 行列 | 多次元配列

方程式の次数。スカラー、ベクトル、行列または多次元配列として指定します。nu は第 2 種ベッセル関数の次数を指定する実数です。nu と Z は同じサイズでなければなりませんが、いずれかをスカラーにすることもできます。

例: bessely(3,0:5)

データ型: single | double

Z — 関数の定義域

スカラー | ベクトル | 行列 | 多次元配列

関数の定義域。スカラー、ベクトル、行列または多次元配列として指定します。bessely は Z が正の場合に実数になります。nu と Z は同じサイズでなければなりませんが、いずれかをスカラーにすることもできます。

例: bessely(1,[1-1i 1+0i 1+1i])

データ型: single | double
複素数のサポート: あり

scale — スケーリング関数への切り替え

0 (既定値) | 1

スケーリング関数に切り替えるかどうか。次の値のいずれかとして指定します。

• 0 (既定) — スケーリングなし

• 1 — bessely の出力を exp(-abs(imag(Z))) でスケーリング

複素平面では、bessely の大きさが abs(imag(Z)) の値の増加に伴い急速に大きくなります。そのため、abs(imag(Z)) の値が大きい場合、出力の指数的なスケーリングが役立ちます。そうしないと、結果の精度が急速に低下したり、倍精度の範囲からオーバーフローしたりします。

例: bessely(3,0:5,1)

詳細

ベッセル関数

次の微分方程式 (ν は実定数) は "ベッセル方程式" と呼ばれています。

$$z^2\frac{d^{2}y}{d{z}^2}+z\frac{dy}{dz}+\left(z^2-{\nu }^2\right)y=0.$$

その解は "ベッセル関数" として知られています。

"第 1 種ベッセル関数" は、J_ν(z) および J_–ν(z) で表され、非整数の ν に対するベッセル方程式の基本解を形成します。J_ν(z) は次で定義されます。

$$J_{\nu }(z)={\left(\frac{z}{2}\right)}^{\nu }{\displaystyle \sum }_{(k=0)}^{\infty }\frac{{\left(\frac{-z^2}{4}\right)}^k}{k!\Gamma (\nu +k+1)}.$$

第 1 種ベッセル関数は besselj を使用して計算できます。

"第 2 種ベッセル関数" は Y_ν(z) で表され、ベッセル方程式の第 2 種の解 (J_ν(z) とは線形独立) を形成します。Y_ν(z) は次で定義されます。

$$Y_{\nu }(z)=\frac{J_{\nu }(z)\cos (\nu \pi )-J_{-\nu }(z)}{\sin (\nu \pi )}.$$

ヒント

ベッセル関数は、第 3 種ベッセル関数とも呼ばれるハンケル関数と密接な関係があります。

$$\begin{array}{l}{H}_{\nu }^{(1)}(z)=J_{\nu }(z)+i{Y}_{\nu }(z)\\ H_{\nu }^{(2)}(z)=J_{\nu }(z)-i{Y}_{\nu }(z).\end{array}$$

$$H_{\nu }^{(K)}(z)$$ は besselh、J_ν(z) は besselj、Y_ν(z) は bessely です。ハンケル関数も、ベッセル方程式の基本解を形成します (besselh を参照)。

参照

[1] Amos, D. E. “Algorithm 644: A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order.” ACM Transactions on Mathematical Software 12, no. 3 (September 1986): 265–273. https://dl.acm.org/doi/10.1145/7921.214331.

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

bessely 関数は tall 配列を完全にサポートしています。詳細については、tall 配列を参照してください。

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• 常に複素数の結果を返します。

• 厳密な単精度計算はサポートされていません。生成されたコードでは、単精度入力で単精度出力が生成されます。ただし、関数内の変数は倍精度である可能性があります。

GPU コード生成

GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

使用上の注意および制限:

• 常に複素数の結果を返します。

• 厳密な単精度計算はサポートされていません。生成されたコードでは、単精度入力で単精度出力が生成されます。ただし、関数内の変数は倍精度である可能性があります。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

bessely 関数は GPU 配列入力をサポートしますが、次の使用上の注意および制限があります。

• 次数 nu は、非負で実数の整数値でなければなりません。

• 引数 Z は、非負の実数値でなければなりません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

この関数は分散配列を完全にサポートしています。詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

besselh | besseli | besselj | besselk