besselh
第 3 種ベッセル関数 (ハンケル関数)
説明
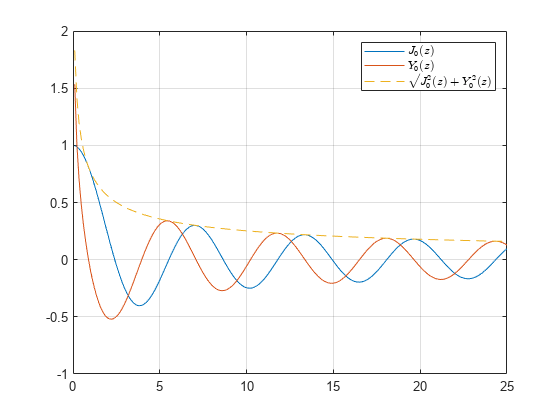
例
入力引数
詳細
参照
[1] Abramowitz, M., and I.A. Stegun. Handbook of Mathematical Functions. National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965.
[2] Amos, D. E. “Algorithm 644: A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order.” ACM Transactions on Mathematical Software 12, no. 3 (September 1986): 265–273. https://dl.acm.org/doi/10.1145/7921.214331.
拡張機能
バージョン履歴
R2006a より前に導入