インターリーブ

ブロック インターリーブ

ブロック インターリーブ機能

ブロック インターリーバーは、セット内のシンボルを繰り返したり省略したりせずに、一連のシンボルを受け取り、再配置します。各セット内のシンボルの数は、与えられたインターリーバーに対して固定されています。一連のシンボルに対するインターリーバーの操作は、他のすべてのセット内のシンボルに対する操作とは無関係です。

インターリーバーは、マッピングに従いシンボルの順序を変えます。対応するデインターリーバーは、逆マッピングを使用して元のシンボル シーケンスを復元します。インターリーブとデインターリーブは、通信システムでのバースト エラーによって引き起こされる誤りを減らすのに役立ちます。

各インターリーバー関数には、対応するデインターリーバー関数があります。インターリーバー/デインターリーバーの組の標準的な利用では、データが再配置されることを除き、デインターリーバーの入力はインターリーバーの入力に一致します。

ブロック インターリーバーは、セット内のシンボルを繰り返したり省略したりせずに、一連のシンボルを受け取り、再配置します。各セット内のシンボルの数は、与えられたインターリーバーに対して固定されています。

このツールボックスのブロック インターリーバーのセットには、いくつかの特別な場合と同様に、一般ブロック インターリーバーが含まれています。特別な場合の各インターリーバー関数は、一般ブロック インターリーバー関数が使用するものと同じ計算コードを使用しますが、特別な場合により適した構文を提供します。インターリーバー関数を、次に説明します。

インターリーバーのタイプ	インターリーバーの機能	説明
一般ブロック インターリーバー	intrlv	入力引数として明示的に指定された置換テーブルを使用します。
代数インターリーバー	algintrlv	Takeshita-Costello 法または Welch-Costas 法を使用して、置換テーブルを代数的に導出します。これらの手法の詳細については、[4]を参照してください。
ヘリカル スキャン インターリーバー	helscanintrlv	行列に対して行ごとにデータを入力してから、行列の内容をらせん状に出力に送ります。
行列インターリーバー	matintrlv	行列に対して行ごとにデータ要素を入力してから、行列の内容を列ごとに出力に送ります。
ランダム インターリーバー	randintrlv	入力した初期状態の入力を使用して置換テーブルをランダムに選択します。

ブロック インターリーバーのタイプ.  このライブラリのブロック インターリーバーのセットには、いくつかの特別な場合と同様に、一般的なインターリーバー/デインターリーバーがあります。特定の場合の各ブロックは、対応するより一般的なブロックが使用するものと同じ計算コードを使用しますが、特定の場合に適したインターフェイスを提供します。

Matrix Interleaver ブロックは、行列に行ごとに入力シンボルを埋め、行列の内容を列ごとに出力端子に送り、ブロック インターリーブを実行します。たとえば、インターリーバーが 2 行 3 列の行列を使用して内部計算を行う場合、ブロックは [1 2 3 4 5 6] の入力に対し、[1 4 2 5 3 6] の出力を生成します。

Random Interleaver ブロックは、ブロック マスクで指定した [Initial seed] パラメーターを使用して置換テーブルをランダムに選択します。同じ [Initial seed] 値を対応する Random Deinterleaver ブロックで使用すると、並べ替えられたシンボルを元の順序に戻すことができます。

Algebraic Interleaver ブロックは代数的に求めた置換テーブルを使用します。このブロックは、Takeshita-Costello インターリーバーと Welch-Costas インターリーバーをサポートします。これらのインターリーバーの詳細については、[4]を参照してください。

MATLAB でブロック インターリーバーを使用したエラー レートの改善

次の例では、チャネルがバースト エラーを生成する通信システムのエラー レートをインターリーバーがどのように改善するかを説明します。ランダム インターリーバーは、2 つの隣り合ったコードワードそれぞれに 3 つのエラーによる誤りが生じる前に、多数のコードワードのビットを再配置します。

エラーが 3 つあると、ハミング符号の誤り訂正能力を越えます。ただし、例は、ハミング符号をインターリーバーと組み合わせると、このシステムは 6 ビットのバースト エラーにもかかわらず元のメッセージを復元できることを示しています。コードワードあたりの誤り数が符号の誤り訂正能力内になるように、インターリーブは異なるコードワード間で効果的に誤りを分散させるので、パフォーマンスが改善されます。

st1 = 27221; st2 = 4831; % States for random number generator
n = 7; k = 4; % Parameters for Hamming code
msg = randi([0 1],k*500,1); % Data to encode
code = encode(msg,n,k,'hamming/binary'); % Encoded data
% Create a burst error that will corrupt two adjacent codewords.
errors = zeros(size(code)); errors(n-2:n+3) = [1 1 1 1 1 1];

% With Interleaving
%------------------
inter = randintrlv(code,st2); % Interleave.
inter_err = bitxor(inter,errors); % Include burst error.
deinter = randdeintrlv(inter_err,st2); % Deinterleave.
decoded = decode(deinter,n,k,'hamming/binary'); % Decode.
disp('Number of errors and error rate, with interleaving:');
[number_with,rate_with] = biterr(msg,decoded) % Error statistics

% Without Interleaving
%---------------------
code_err = bitxor(code,errors); % Include burst error.
decoded = decode(code_err,n,k,'hamming/binary'); % Decode.
disp('Number of errors and error rate, without interleaving:');
[number_without,rate_without] = biterr(msg,decoded) % Error statistics

例からの出力は以下のようになります。

Number of errors and error rate, with interleaving:

number_with =

     0


rate_with =

     0

Number of errors and error rate, without interleaving:

number_without =

     4


rate_without =

    0.0020

Simulink でブロック インターリーバーを使用したエラー レートの改善

次の例では、インターリーバーを使用してチャネルがバースト エラーを生成するときのエラー レートを改善する方法を説明します。

モデルを実行する前に、Simulink でブロック インターリーバーを使用したエラー レートの改善で説明されているように、バースト エラーをシミュレートするバイナリ ベクトルを作成しなければなりません。Signal From Workspace ブロックはこのベクトルを MATLAB ワークスペースからモデルにインポートし、ここで、Logical Operator ブロックは信号を使用してベクトルの XOR を実行します。

モデルを作成するには、次のブロックを収集し、設定します。

• Bernoulli Binary Generator

  • [Frame-based outputs] の隣にあるボックスをオンにします。

  • [フレームあたりのサンプル数] を 4 に設定します。

• Hamming Encoder (既定のパラメーター設定)。

• Buffer (パラメーター設定を次のように更新):

  • [Output buffer size (per channel)] を 84 に設定します。

• Random Interleaver

  • [Number of elements] を 84 に設定します。

• Logical Operator (Simulink) (パラメーター設定を次のように更新):

  • [Operator] を [XOR] に設定します。

• Signal From Workspace (パラメーター設定を次のように更新):

  • [Signal] を errors に設定します。

  • [サンプル時間] を 4/7 に設定します。

  • [フレームあたりのサンプル数] を 84 に設定します。

• Random Deinterleaver (パラメーター設定を次のように更新):

  • [Number of elements] を 84 に設定します。

• Buffer (パラメーター設定を次のように更新):

  • [Output buffer size (per channel)] を 7 に設定します。

• Hamming Decoder (既定のパラメーター設定)。

• Error Rate Calculation (パラメーター設定を次のように更新):

  • [Receive delay] を (4/7)*84 に設定します。

  • [Computation delay] を 100 に設定します。

  • [Output data] を [Port] に設定します。

• Display (Simulink) (既定のパラメーター設定)。

[シミュレーション] タブの [シミュレーション] セクションで、[終了時間] を length(errors) に設定します。[シミュレーション] セクションは複数のタブに表示されます。

誤差のベクトルの作成.  モデルを実行する前に、次のコードを使用して MATLAB ワークスペースでバイナリ ベクトルを作成します。モデルはこのベクトルを使用して、バースト エラーをシミュレートします。ベクトルには 3 つの 1 で構成されるブロックが含まれており、それぞれがランダムな間隔でのバースト エラーを表しています。1 で構成される 2 つの連続したブロック間の距離は、1 ～ 80 までの整数乱数です。

errors=zeros(1,10^4);
n=1;
while n<10^4-80;
n=n+floor(79*rand(1))+3;
errors(n:n+2)=[1 1 1];
end

ベクトル errors 内のシンボル総数に対する 1 の数の割合を特定するには、以下を入力します。

sum(errors)/length(errors)

正しい割合は約 3/43 または 0.0698 になります。これは、3 つの 1 で構成される各シーケンスの後、1 で構成される次のシーケンスまでの予想距離が 40 になるためです。この結果、43 個のシーケンスの項で 3 つの 1 が予想されます。モデルに誤り訂正がない場合は、ビット エラー レートはおよそ .0698 になります。

モデルでシミュレーションを実行すると、誤り訂正とインターリーブによって、エラー レートはおよそ .019 となり改善されます。Random Interleaver および Random Deinterleaver ブロックをモデルから削除し、ラインを接続し、別のシミュレーションを実行すると、インターリーブの効果を確認できます。ハミング符号は各コードワードで 1 つの誤りしか訂正できないため、ビット エラー レートはインターリーブを使用しないと高くなります。

畳み込みインターリーブ

畳み込みインターリーブ機能

畳み込みインターリーバーは、それぞれが一定の遅延をもつ、一連のシフト レジスタで構成されます。一般多重インターリーバーは遅延の値が制限されませんが、標準的な畳み込みインターリーバーの遅延は、一定の整数の非負整数倍です。入力ベクトルからの新しいシンボルはそれぞれ、次のシフト レジスタに入力され、そのレジスタ内の最も古いシンボルは出力ベクトルの一部になります。畳み込みインターリーバーにはメモリがあります。つまり、その操作は、現在のシンボルのみでなく前のシンボルにも依存します。

畳み込みインターリーバーと畳み込みデインターリーバーのペアによる合計遅延は N × slope × (N – 1) です。

• N はレジスタの数

• slope はレジスタの長さのステップ

次の図は、シフト レジスタのセットで構成される一般的な畳み込みインターリーバーの構造を示しています。各シフト レジスタには、D(1)、D(2)、...、D(N) として示される指定された遅延と、入力を切り替え、レジスタを経由してシンボルを出力するコミュテーターがあります。k 番目のシフト レジスタは D(k) 個のシンボルを保持します。ここで k = 1, 2, 3, … N です。k 番目のシフト レジスタの遅延値は ((k–1) × slope) です。新しい入力シンボルごとに、コミュテーターは新しいレジスタに切り替わり、新しいシンボルをシフトインしながら、そのレジスタ内の最も古いシンボルをシフトアウトします。コミュテーターが N 番目のレジスタに到達し、次の新しい入力が発生すると、コミュテーターは最初のレジスタに戻ります。

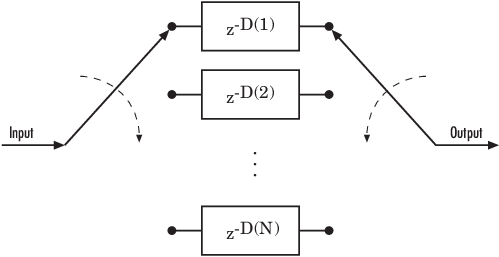
Communications Toolbox™ は、Simulink^® ブロック、System object、および関数 MATLAB^® を使用して畳み込みインターリーブ機能を実装します。このツールボックスの畳み込みインターリーバーは、シフト レジスタの番号と各シフト レジスタに対する遅延を表す入力引数をもちます。

この製品の畳み込みインターリーバーのセットには、いくつかの特別な場合と同様に、一般的なインターリーバー/デインターリーバーがあります。特定の場合の各関数は、対応するより一般的な関数が使用するものと同じ計算コードを使用しますが、特定の場合に適した構文を提供します。特定の場合を次に説明します。

インターリーバーのタイプ	インターリーブ関数	説明
一般多重インターリーバー	muxintrlv	シフト レジスタのセットに対して制限のない遅延値を使用できます。
畳み込みインターリーバー	convintrlv	シフト レジスタのセットに対する遅延値は、指定した一定の整数の非負整数倍です。
ヘリカル インターリーバー	helintrlv	らせん状に配列に入力シンボルを入力し、行ごとに配列を空にします。

関数 helscanintrlv および helintrlv は、いずれも内部的な計算に対してヘリカル配列を使用します。ただし、2 つの関数には重要な違いがあります。

• helintrlv は、行に制限のない配列を使用し、列に沿って配列に入力シンボルを配置します。現在の入力からのものではないシンボルをいくつか出力し、入力シンボルの一部を出力に含めずに配列に残します。

• helscanintrlv は、固定サイズの行列を使用し、配列の各行で入力シンボルを配置して、既定値または前の呼び出しからの値を使用せずに、すべての入力シンボルを出力します。

畳み込みインターリーバーのタイプ.  このライブラリの畳み込みインターリーバーのセットには、いくつかの特別な場合と同様に、一般的なインターリーバー/デインターリーバーがあります。特定の場合の各ブロックは、対応するより一般的なブロックが使用するものと同じ計算コードを使用しますが、特定の場合に適したインターフェイスを提供します。

このライブラリで最も一般的なブロックは General Multiplexed Interleaver ブロックです。このブロックでは、シフト レジスタのセットに対して任意の遅延値を指定できます。このブロックを使用して前の回路図を実装するには、[D(1); D(2); ...; D(N)] の [Interleaver delay] パラメーターを使用します。

より具体的には Convolutional Interleaver ブロックを使用します。このブロック内では、k 番目のシフト レジスタの遅延値はブロックの [Register length step] パラメーターの (k-1) 倍になります。このブロック内のシフト レジスタの数は、[Rows of shift registers] パラメーターの値です。

最後に、Helical Interleaver ブロックはらせん状に配列にシンボルを入力し、行ごとに配列を空にする特殊な畳み込みインターリーブをサポートします。インターリーバーを設定するには、[ヘリカル配列の列数] パラメーターを使用して配列の幅を設定し、[Group size] と [ヘリカル配列のステップ サイズ] パラメーターを使用してシンボルが配列でどのように配置されるかを特定します。詳細と例は、Helical Interleaver ブロックのリファレンス ページを参照してください。

畳み込みインターリーバーの遅延

シンボルのシーケンスが畳み込みインターリーバーと対応する畳み込みデインターリーバーを通過した後、復元されたシーケンスは元のシーケンスより遅れます。次の表は、シンボルで測定される元のシーケンスと復元されたシーケンスの間の遅延をまとめています。2 番目の列の変数名 (delay、nrows、slope、col、ngrp、および stp) は、各関数のリファレンス ページに示されている入力を参照します。

インターリーバー/デインターリーバー ペアの遅延

インターリーバー/デインターリーバー ペア	元のシーケンスと復元されたシーケンスの間の遅延
muxintrlv, muxdeintrlv	length(delay)*max(delay)
convintrlv, convdeintrlv	nrows*(nrows-1)*slope
helintrlv, heldeintrlv	col*ngrp*ceil(stp*(col-1)/ngrp)

畳み込みインターリーバーの遅延.  シンボルのシーケンスが畳み込みインターリーバーと対応する畳み込みデインターリーバーを通過した後、復元されたシーケンスは元のシーケンスより遅れます。一般多重インターリーバーのほとんどでは、シンボルで測定される元のシーケンスと復元されたシーケンスの間の遅延は次の式で表されます。

シフト レジスタ数 × すべてのシフト レジスタ間の最大遅延

モデルのインターリーバー出力とデインターリーバー入力間で追加の遅延が発生した場合は、復元されたシーケンスは、追加の遅延と上述の式による遅延を足した分だけ元のシーケンスより遅れます。

メモ

同期が正しく行われるためには、モデルのインターリーバー出力とデインターリーバー入力間の遅延は、シフト レジスタ数の整数倍でなければなりません。DSP System Toolbox™ Delay ブロックを使用すると、必要に応じて遅延を手動で調整できます。

Convolutional Interleaver ブロック

Convolutional Interleaver/Convolutional Deinterleaver のペアによって実装される特殊なケースでは、シフト レジスタの数は [Rows of shift registers] パラメーターですが、すべてのシフト レジスタ間の最大遅延は、次の式で表されます。

B × (N-1)

ここで、B は [Register length step] パラメーターで、N は [Rows of shift registers] パラメーターです。

Helical Interleaver ブロック

Helical Interleaver/Helical Deinterleaver のペアで実装される特殊なケースでは、復元されたシーケンスと元のシーケンス間の遅延は、次の式で表されます。

$$CN\lceil \frac{s(C-1)}{N}\rceil$$

ここで、C は [ヘリカル配列の列数] パラメーター、N は [Group size] パラメーター、s は [ヘリカル配列のステップ サイズ] パラメーターです。

MATLAB を使用して畳み込みインターリーブされたデータの再生に対する遅延の影響.  畳み込みインターリーバーの後に対応する畳み込みデインターリーバーを使用する場合、遅延がゼロでないことは、復元されたデータ (つまり、デインターリーバーからの出力) が元のデータ (つまり、インターリーバーへの入力) と同じではないことを意味します。2 つのデータ セットを直接比較する場合、適切な切り捨てまたはパディング操作を行って遅延を考慮しなければなりません。

インターリーバー/デインターリーバーのペアで遅延 D を補正する標準的な方法がいくつかあります。

• 元のデータの末尾に余分な D 個のシンボルを付加してインターリーブする。元のデータを復元されたデータと比較する前に、復元されたデータの最初の D 個のシンボルを省略する。この方法では、元のシンボルはすべて、復元されたデータに現れます。

• 元のデータを復元されたデータと比較する前に、元のデータの最後の D 個のシンボルと、復元されたデータの最初の D 個のシンボルを省略する。この方法では、元のシンボルのいくつかは、デインターリーバーのシフト レジスタに残され、復元されたデータには現れません。

次のコードは、インターリーブ/デインターリーブ操作のシンボル エラー レートを計算することによって、これらの方法を説明します。

x = randi([0 63],20,1); % Original data
nrows = 3; slope = 2; % Interleaver parameters
D = nrows*(nrows-1)*slope; % Delay of interleaver/deinterleaver pair
hInt   = comm.ConvolutionalInterleaver('NumRegisters', nrows, ...
                    'RegisterLengthStep', slope);
hDeint = comm.ConvolutionalDeinterleaver('NumRegisters', nrows, ...
                    'RegisterLengthStep', slope);

% First approach.
x_padded = [x; zeros(D,1)]; % Pad x at the end before interleaving.
a1 = step(hInt, x_padded); % Interleave padded data.

b1 = step(hDeint, a1)
% Omit input padding and the first D symbols of the recovered data and
% compare
servec1 = step(comm.ErrorRate('ReceiveDelay',D),x_padded,b1);
ser1 = servec1(1)

% Second approach.
release(hInt); release(hDeint)
a2 = step(hInt,x); % Interleave original data.
b2 = step(hDeint,a2)
% Omit the last D symbols of the original data and the first D symbols of
% the recovered data and compare.
servec2 = step(comm.ErrorRate('ReceiveDelay',D),x,b2);
ser2 = servec2(1)

出力は、以下のとおりです。ser1 と ser2 の値 0 は、シンボル エラー レートを計算する前に、スクリプトが元のデータと復元されたデータを正しく並べることを示します。ただし、b1 と b2 の長さから、2 つの配置方法では、デインターリーブされたデータの長さが異なることに注意してください。

b1 =

     0
     0
     0
     0
     0
     0
     0
     0
     0
     0
     0
     0
    59
    42
     1
    28
    52
    54
    43
     8
    56
     5
    35
    37
    48
    17
    28
    62
    10
    31
    61
    39


ser1 =

     0


b2 =

     0
     0
     0
     0
     0
     0
     0
     0
     0
     0
     0
     0
    59
    42
     1
    28
    52
    54
    43
     8


ser2 =

     0

インターリーブ遅延と他の遅延を組み合わせる.  インターリーバー出力とデインターリーバー入力の間に、さらに遅延 d (たとえば、フィルターからの遅延) を引き起こすスクリプトで畳み込みインターリーバーを使用する場合、d と表インターリーバー/デインターリーバー ペアの遅延からの値の合計だけ、復元されたシーケンスは元のシーケンスより遅れます。この場合、d はシフト レジスタ数の整数倍でなければなりません。そうでない場合、畳み込みデインターリーバーは、元のシンボルを適切に復元できません。d がシフト レジスタ数の整数倍でない場合、デインターリーバーへの入力となるベクトルを付加することによって、遅延を手作業で調整できます。

MATLAB で連続した整数のシーケンスを使用した畳み込みインターリーブとデインターリーブ

下記の例は、連続した整数のシーケンスを使用した、畳み込みインターリーブとデインターリーブを説明します。また、インターリーバー/デインターリーバーのペアに固有の遅延も説明します。

x = [1:10]'; % Original data
delay = [0; 1; 2]; % Set delays of three shift registers.
hInt = comm.MultiplexedInterleaver('Delay', delay);
hDeint = comm.MultiplexedDeinterleaver('Delay', delay);
y = step(hInt,x) % Interleave.
z = step(hDeint,y) % Deinterleave.

この例では、関数 muxintrlv は、3 つのシフト レジスタをそれぞれ []、[0]、および [0 0] の値に初期化します。その後、この関数は次の表に示すように内部的な計算を実行して、入力データ [1:10]' を処理します。

現在の入力	現在のシフト レジスタ	現在の出力	シフト レジスタの内容
1	1	1	[] [0] [0 0]
2	2	0	[] [2] [0 0]
3	3	0	[] [2] [0 3]
4	1	4	[] [2] [0 3]
5	2	2	[] [5] [0 3]
6	3	0	[] [5] [3 6]
7	1	7	[] [5] [3 6]
8	2	5	[] [8] [3 6]
9	3	3	[] [8] [6 9]
10	1	10	[] [8] [6 9]

例からの出力は以下のようになります。

y =

     1
     0
     0
     4
     2
     0
     7
     5
     3
    10


state_y =

    value: {3x1 cell}
    index: 2


z =

     0
     0
     0
     0
     0
     0
     1
     2
     3
     4

上の表の列 "現在の出力" は、ベクトル y の値と一致することに注意してください。さらに、上の表の最後の行は、与えられたデータ セットに対して処理された最後のシフト レジスタが 1 番目のシフト レジスタであることを示します。これは、state_y.index の値が 2 であることに合致し、追加された入力データが 2 番目のシフト レジスタに割り当てられることを示します。例を実行した後にコマンド ウィンドウで state_y.value と入力すると、state_y.value{:} にリストされた状態の値が表の最後の行の項目 "シフト レジスタの内容" に一致することを確認できます。

例の出力のその他の特徴として、z は元のデータ セットからのシンボルを含む前に先頭に 6 個の 0 を含むことに注意してください。6 個の 0 は、この畳み込みインターリーバー/デインターリーバーのペアの遅延が length(delay)*max(delay) = 3*2 = 6 であることを示します。遅延の詳細については、畳み込みインターリーバーの遅延を参照してください。

Simulink で連続した整数のシーケンスを使用した畳み込みインターリーブとデインターリーブ

下記の例は、連続した整数のシーケンスを使用した、畳み込みインターリーブとデインターリーブを説明します。また、インターリーブ ブロックの初期条件に固有の遅延および影響についても説明します。

モデルを作成するには、次のブロックを収集し、設定します。

• Ramp (Simulink) (既定のパラメーター設定)。

• Zero-Order Hold (Simulink) (既定のパラメーター設定)。

• Convolutional Interleaver (パラメーター設定を次のように更新):

  • [Rows of shift registers] を 3 に設定します。

  • [Initial conditions] を [-1 -2 -3]' に設定します。

• Convolutional Deinterleaver (パラメーター設定を次のように更新):

  • [Rows of shift registers] を 3 に設定します。

  • [Initial conditions] を [-1 -2 -3]' に設定します。

• To Workspace (Simulink) の 2 つのコピー (パラメーター設定を次のように更新):

  • このブロックの 2 つのコピーで [変数名] をそれぞれ interleaved と restored に設定します。

  • このブロックの 2 つのコピーのそれぞれで [保存形式] を [配列] に設定します。

  ヒント

  To Workspace ブロックを DSP System Toolbox / Sinks サブライブラリから選択します。詳細については、通信システム シミュレーション用の To Workspace ブロックの構成を参照してください。

[シミュレーション] タブの [シミュレーション] セクションで、[終了時間] を 20 に設定します。[シミュレーション] セクションは複数のタブに表示されます。シミュレーションを実行し、次のコマンドを実行します。

comparison = [[0:20]', interleaved, restored]

comparison =

     0     0    -1
     1    -2    -2
     2    -3    -3
     3     3    -1
     4    -2    -2
     5    -3    -3
     6     6    -1
     7     1    -2
     8    -3    -3
     9     9    -1
    10     4    -2
    11    -3    -3
    12    12     0
    13     7     1
    14     2     2
    15    15     3
    16    10     4
    17     5     5
    18    18     6
    19    13     7
    20     8     8

この出力では、最初の列には元のシンボル シーケンスが含まれます。2 つ目の列には、インターリーブされたシーケンス、そして 3 つ目の列には復元されたシーケンスが含まれます。

インターリーブおよび復元されたシーケンスの負の数値は、元のデータではなくインターリーブ ブロックの初期条件から取得されたものです。元のシンボルの最初のシンボルは 12 シンボルの遅延の後でのみ復元されたシーケンスに含まれます。インターリーバー/デインターリーバーの組み合わせの遅延は、シフト レジスタ数 (3) とすべてのシフト レジスタ間の最大遅延 (4) の積です。

プロセスの各ステップでのシフト レジスタのコンテンツを示す同様な例は、MATLAB で連続した整数のシーケンスを使用した畳み込みインターリーブとデインターリーブを参照してください。

インターリーブの参考文献

[1] Berlekamp, E.R., and P. Tong, “Improved Interleavers for Algebraic Block Codes,” U. S. Patent 4559625, Dec. 17, 1985.

[2] Clark, George C., and J. Bibb Cain. Error-Correction Coding for Digital Communications. Applications of Communications Theory. New York: Plenum Press, 1981.

[3] Forney, G. D. Jr., “Burst-Correcting Codes for the Classic Bursty Channel,” IEEE Transactions on Communications, vol. COM-19, October 1971, pp. 772-781.

[4] Heegard, Chris and Stephen B. Wicker. Turbo Coding. Boston: Kluwer Academic Publishers, 1999.

[5] Ramsey, J. L, “Realization of Optimum Interleavers,” IEEE Transactions on Information Theory, IT-16 (3), May 1970, pp. 338-345.

[6] Takeshita, O. Y. and D. J. Costello, Jr., “New Classes Of Algebraic Interleavers for Turbo-Codes,” Proc. 1998 IEEE International Symposium on Information Theory, Boston, Aug. 16–21, 1998. pp. 419.