このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

ビット エラー レート解析の手法

このトピックでは、さまざまな通信システムの誤りの統計を計算する方法について説明します。

理論上の誤り統計の計算

シミュレーション データを使用した SER と BER の計算のセクションで説明している関数 biterr は、実測誤り統計を収集できるだけでなく、それらの結果を理論上の誤り統計と比較して検証するのにも役立ちます。ある種の通信システムには、ビット エラー レート (BER) または BER の近似範囲の計算に関して閉形式表現が存在します。次の表に記載された関数は、指定の種類の通信システムにおいて、BER またはその範囲に関する閉形式表現を計算します。

通信システムの種類	関数
符号化されていない AWGN チャネル	berawgn
符号化されていないレイリーおよびライス フェージング チャネル	berfading
符号化された AWGN チャネル	bercoding
不完全な同期の符号化されていない AWGN チャネル	bersync

これらの関数で使用される解析的表現については、BER 解析で使用される解析的表現で説明しています。これらの関数のリファレンス ページには、関数で実装される閉形式表現が説明された 1 つ以上の書籍も掲載されています。

理論上の性能結果

• 理論上のエラー レートのプロット

• 理論上のエラー レートと実測エラー レートの比較

理論上のエラー レートのプロット

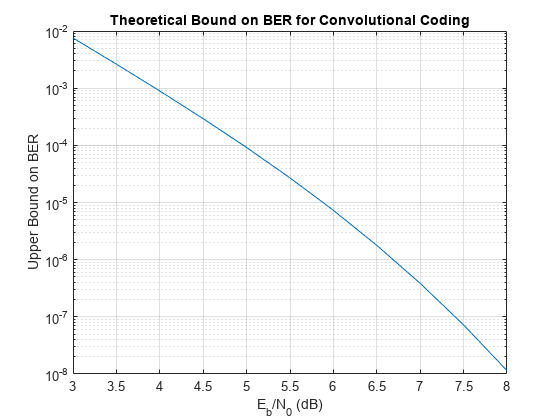
この例では、関数bercodingを使用して、軟判定復号化器による畳み込み符号化の BER の上限を計算します。

coderate = 1/4; % Code rate

距離スペクトルに関する情報を含む構造体 dspec を作成します。ビットあたりのエネルギー対ノイズ パワー スペクトル密度比 (${\mathit{E}}_{\mathit{b}}/{\mathit{N}}_0$) のスイープ範囲を定義し、理論的な限界の結果を生成します。

dspec.dfree = 10; % Minimum free distance of code
dspec.weight = [1 0 4 0 12 0 32 0 80 0 192 0 448 0 1024 ...
    0 2304 0 5120 0]; % Distance spectrum of code
EbNo = 3:0.5:8;
berbound = bercoding(EbNo,'conv','soft',coderate,dspec);

理論的な限界の結果をプロットします。

semilogy(EbNo,berbound)
xlabel('E_b/N_0 (dB)'); 
ylabel('Upper Bound on BER');
title('Theoretical Bound on BER for Convolutional Coding');
grid on;

理論上のエラー レートと実測エラー レートの比較

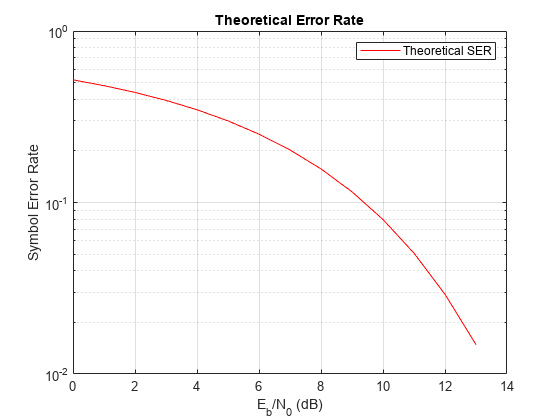
関数berawgnを使用して、${\mathit{E}}_{\mathit{b}}/{\mathit{N}}_0$ 値の範囲におけるパルス振幅変調 (PAM) の理論上のシンボル エラー レート (SER) を計算します。8 PAM を AWGN チャネルでシミュレートし、実測 SER を計算します。その後、理論および実測による SER を同一の座標軸セット上にプロットして比較します。

berawgnを使用して、理論上の SER を計算してプロットします。

rng('default') % Set random number seed for repeatability
M = 8;
EbNo = 0:13;
[ber,ser] = berawgn(EbNo,'pam',M);

semilogy(EbNo,ser,'r');
legend('Theoretical SER');
title('Theoretical Error Rate');
xlabel('E_b/N_0 (dB)');
ylabel('Symbol Error Rate');
grid on;

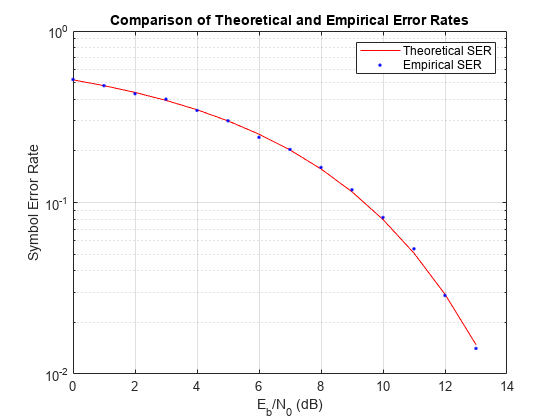
8 PAM 通信システム リンクをシミュレートして実測 SER を計算します。シミュレーション パラメーターを定義し、結果に必要な変数を事前に割り当てます。[1]で説明されているように、${\mathit{N}}_0=2\times {\left({\mathit{N}}_{\mathrm{Variance}}\right)}^2$ であるため、${\mathit{E}}_{\mathit{b}}/{\mathit{N}}_0$ 値を SNR 値に変換するときに ${\mathit{E}}_{\mathit{b}}/{\mathit{N}}_0$ 値に 3 dB を追加します。

n = 10000; % Number of symbols to process
k = log2(M); % Number of bits per symbol
snr = EbNo+3+10*log10(k); % In dB
ynoisy = zeros(n,length(snr));
z = zeros(n,length(snr));
errVec = zeros(3,length(EbNo));

エラー レート計算機 System object™ を作成して、復号化されたシンボルを元の送信シンボルと比較します。

errcalc = comm.ErrorRate;

ランダム データ メッセージを生成して PAM を適用します。チャネルを信号強度に正規化します。シミュレーションをループ処理し、SNR 値の範囲におけるエラー レートを生成します。

x = randi([0 M-1],n,1); % Create message signal
y = pammod(x,M); % Modulate
signalpower = (real(y)'*real(y))/length(real(y));

for jj = 1:length(snr)
    reset(errcalc)
    ynoisy(:,jj) = awgn(real(y),snr(jj),'measured'); % Add AWGN
    z(:,jj) = pamdemod(complex(ynoisy(:,jj)),M); % Demodulate
    errVec(:,jj) = errcalc(x,z(:,jj)); % Compute SER from simulation
end

理論上の結果と実測結果を比較します。

hold on;
semilogy(EbNo,errVec(1,:),'b.');
legend('Theoretical SER','Empirical SER');
title('Comparison of Theoretical and Empirical Error Rates');
hold off;

シミュレーションによる性能結果

• この節の概要

• シミュレーション データを使用した SER と BER の計算

この節の概要

この節では、通信システムのシミュレーションに出入りするデータ メッセージを比較する方法、およびモンテカルロ法を使用して誤りの統計を計算する方法について説明します。送信前と受信後のデータ メッセージを使用して通信システムの BER または SER を測定することで、システム性能をシミュレーションで測定できます。通信システムのモデル化とシミュレーションに使用される物理レイヤーのコンポーネントについて調べるには、PHY コンポーネントを参照してください。

小規模または不完全なデータ セットしかない場合に、滑らかな曲線をプロットしてプレゼンテーションを行いたいときには、曲線近似が役立つことがあります。シミュレーションによる性能結果の計算で曲線近似を使用する方法について調べるには、エラー レート プロットの曲線近似の節を参照してください。

シミュレーション データを使用した SER と BER の計算

この例では、関数biterrとsymerrをそれぞれ使用して SER と BER を計算する方法を示します。関数symerrは 2 組のデータを比較して、シンボル誤りの数と SER を計算します。関数biterrは 2 組のデータを比較して、ビット エラーの数と BER を計算します。誤りとは 2 組のデータの対応するポイントにおける相違を意味します。

2 組のデータとは、通常は送信側に入力されるメッセージと受信側から出力される復元されたメッセージです。通信システムの別の部分に出入りするデータ (符号化器の入力データと復号化器の出力データなど) を比較することもできます。

通信システムで 1 つのシンボルを表現するのに複数ビットが使用されている場合は、シンボル誤り数とビット エラー数が異なります。シンボルまたはビットのいずれを計数する場合でも、エラー レートとは送信されたシンボルまたはビットの総数でエラー数を割った値になります。

一般に、少なくとも 100 の誤りが生成されるように十分なデータを使用してシミュレートすると正確なエラー レートが得られます。エラー レートがきわめて低いときは (たとえば、${10}^{-6}$ 以下)、半解析的手法を使用するとシミュレーションのみの場合よりも高速に結果を計算できる場合があります。詳細については、半解析的手法による性能結果の節を参照してください。

エラー レートの計算

関数symerrを使用して、ノイズを含む線形ブロック符号の SER を計算します。デジタル変調は適用せず、各シンボルに 1 ビットずつ含まれるようにします。各シンボルが 1 ビットの場合、シンボル誤りとビット エラーは同じになります。

符号化されたメッセージに人為的にノイズを追加し、その結果生じたノイズを含む符号を元の符号と比較します。次に、復号化を行い、復号化されたメッセージを元のメッセージと比較します。

m = 3; % Set parameters for Hamming code
n = 2^m-1;
k = n-m;
msg = randi([0 1],k*200,1); % Specify 200 messages of k bits each
code = encode(msg,n,k,'hamming');
codenoisy = bsc(code,0.95); % Add noise
newmsg = decode(codenoisy,n,k,'hamming'); % Decode and correct errors

SER を計算します。

[~,noisyVec] = symerr(code,codenoisy);
[~,decodedVec] = symerr(msg,newmsg);

復号化後は、復号化器構成の誤り訂正能力に基づいてハミング復号化器によって誤りが訂正されるため、エラー レートが減少します。メッセージは乱数発生器で生成され、ノイズも加わるため、結果は実行するたびに異なります。SER を表示します。

disp(['SER in the received code: ',num2str(noisyVec(1))])

SER in the received code: 0.94571

disp(['SER after decoding: ',num2str(decodedVec(1))])

SER after decoding: 0.9675

SER と BER の比較

以下のコマンドは、さまざまな状況でのシンボル誤りとビット エラーの違いを示しています。

3 要素の 10 進数ベクトルを 2 つ作成し、バイナリ表現を表示します。ベクトル a には 2 ビットのシンボルを 3 つ、ベクトル b には 3 ビットのシンボルを 3 つ格納します。

bpi = 3; % Bits per integer
a = [1 2 3]; 
b = [1 4 4];
int2bit(a,bpi)

ans = 3×3

     0     0     0
     0     1     1
     1     0     1

int2bit(b,bpi)

ans = 3×3

     0     1     1
     0     0     0
     1     0     0

2 つのベクトルのバイナリ値を比較し、関数biterrおよびsymerrを使用して誤り数とエラー レートを計算します。

format rat % Display fractions instead of decimals
[snum,srate] = symerr(a,b)

snum = 
       2       

srate = 
       2/3     

2 番目と 3 番目のエントリのビットが異なるため、snum は 2 です。合計シンボル数は 3 であるため、srate は 2/3 になります。

[bnum,brate] = biterr(a,b)

bnum = 
       5       

brate = 
       5/9     

2 番目のエントリは 2 ビット、3 番目のエントリは 3 ビット異なるため、bnum は 5 です。合計ビット数が 9 なので、brate は 5/9 で表されます。ビット数の合計は、a (シンボル誤りの計算の場合) または b (ビット エラーの計算の場合) のエントリ数に a と b のすべてのエントリにおける最大ビット数を掛けた値として定義されます。

半解析的手法による性能結果

シミュレーションによる性能結果の節で説明されている手法は、さまざまな通信システムで動作しますが、エラー レートが低い場合には (たとえば、10^-6 以下)、計算に膨大な時間がかかる可能性があります。エラー レートを計算する代替方法として半解析的手法があります。半解析的手法を使用すると、シミュレートされたデータを使用する非解析的手法よりも迅速に結果が得られます。

シミュレーションと解析を組み合わせて使用することによって通信システムのエラー レートを決定する半解析的手法の実装の詳細については、関数 semianalytic を参照してください。

エラー レートのプロット

• この節の概要

• 関数 semilogy を使用したエラー レート プロットの作成

• エラー レート プロットの曲線近似

• エラー レート プロットでの曲線近似の使用

この節の概要

エラー レートのプロットは、通信システムの性能を検証する場合に役立ち、多くの出版物でも取り入れられています。この節では、エラー レート プロットの作成に使用できるツールについて説明します。それらをニーズに合わせて変更し、エラー レート データに対する曲線近似とプロットを実行する方法を示します。

関数 semilogy を使用したエラー レート プロットの作成

エラー レート プロットの多くは、水平軸に E_b/N₀ 値 (dB) をとり、垂直軸にエラー レートを 10 を底とする対数で表します。このようなプロットを関数 semilogy を使用して作成する例については、理論上のエラー レートと実測エラー レートの比較および理論上のエラー レートのプロットを参照してください。

エラー レート プロットの曲線近似

小規模または不完全なデータ セットしかない場合に、滑らかな曲線をプロットしてプレゼンテーションを行いたいときには、曲線近似が役立つことがあります。関数 berfit には、実測データがさまざまな E_b/N₀ 値におけるエラー レートを示している場合の解析に役立つ曲線近似の機能が含まれています。この関数により以下が可能です。

• 近似の生成に使用される閉形式関数の種類を選択する一覧など、曲線近似プロセスのさまざまな関連局面のカスタマイズ。

• berfit がデータに近似させる曲線に沿った、実測データのプロット。

• 実測データ セットの E_b/N₀ 値間の近似曲線上に点を内挿してプロットを平滑化。

• 近似曲線に沿った点の数値や近似式の係数など、近似に関連する情報の収集。

メモ

関数 berfit は、外挿ではなく、曲線近似または内挿を目的としています。最小実測 BER 値より 1 桁小さい値以上の BER データを外挿すると、本質的に信頼性が低くなります。

エラー レート プロットでの曲線近似の使用

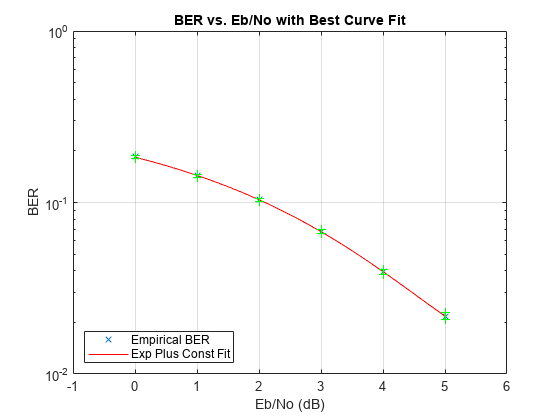
この例では、単純な差動 2 位相偏移変調 (DBPSK) 通信システムをシミュレートし、一連の ${\mathit{E}}_{\mathrm{b}}/{\mathit{N}}_0$ 値に対応するエラー レート データをプロットします。関数berfitおよびberconfintを使用して、実測エラー レートの集合を曲線で近似します。

シミュレーション パラメーターの初期化

入力信号メッセージ長、変調次数、シミュレートする ${\mathit{E}}_{\mathrm{b}}/{\mathit{N}}_0$ 値の範囲、およびシミュレーションがその ${\mathit{E}}_{\mathrm{b}}/{\mathit{N}}_0$ 値に対するエラー レートを計算する前に発生しなければならない誤り数の最小数を指定します。最終結果と中間結果の変数を事前に割り当てます。

一般に、エラー レートの結果を統計的に正確なものにするには、誤り数の最小数を 100 のオーダーにする必要があります。このシミュレーションでは、少ない誤り数を使用して実行時間を短縮し、結果のセットを曲線近似で平滑化する方法を示します。

siglen = 100000; % Number of bits in each trial
M = 2; % DBPSK is binary
EbN0vec = 0:5; % Vector of EbN0 values
minnumerr = 5; % Compute BER after only 5 errors occur
numEbN0 = length(EbN0vec); % Number of EbN0 values

ber = zeros(1,numEbN0); % Final BER values
berVec = zeros(3,numEbN0); % Updated BER values
intv = cell(1,numEbN0); % Cell array of confidence intervals

エラー レート計算機 System object™ を作成します。

errorCalc = comm.ErrorRate;

シミュレーションのループ処理

DBPSK 変調された通信システムをシミュレートし、for ループを使用して ${\mathit{E}}_{\mathrm{b}}/{\mathit{N}}_0$ 値に変化を与えて BER を計算します。内側の while ループで、各 ${\mathit{E}}_{\mathrm{b}}/{\mathit{N}}_0$ 値に対して最小数のビット エラーが必ず発生するようにします。各 ${\mathit{E}}_{\mathrm{b}}/{\mathit{N}}_0$ 値のエラー レートの統計が保存されます。これをこの例の後半で曲線近似およびプロットを実行するときに使用します。

for jj = 1:numEbN0
    EbN0 = EbN0vec(jj);
    snr = EbN0; % For binary modulation SNR = EbN0
    reset(errorCalc)
    
    while (berVec(2,jj) < minnumerr)
        msg = randi([0,M-1],siglen,1); % Generate message sequence
        txsig = dpskmod(msg,M); % Modulate
        rxsig = awgn(txsig,snr,'measured'); % Add noise
        decodmsg = dpskdemod(rxsig,M); % Demodulate
        berVec(:,jj) = errorCalc(msg,decodmsg); % Calculate BER
    end

関数berconfintを使用して、${\mathrm{E}}_{\mathrm{b}}/{\mathit{N}}_0$ 値に対する 98% の信頼区間でのエラー レートを計算します。

    [ber(jj),intv1] = berconfint(berVec(2,jj),berVec(3,jj),0.98);
    intv{jj} = intv1;
    disp(['EbN0 = ' num2str(EbN0) ' dB, ' num2str(berVec(2,jj)) ...
        ' errors, BER = ' num2str(ber(jj))])
end

EbN0 = 0 dB, 18427 errors, BER = 0.18427
EbN0 = 1 dB, 14322 errors, BER = 0.14322
EbN0 = 2 dB, 10384 errors, BER = 0.10384
EbN0 = 3 dB, 6789 errors, BER = 0.06789
EbN0 = 4 dB, 3945 errors, BER = 0.03945
EbN0 = 5 dB, 2175 errors, BER = 0.02175

関数berfitを使用して、プロットを平滑化するために BER 点間の内挿を行い、最良の近似曲線をプロットします。プロットに信頼区間を追加します。

fitEbN0 = EbN0vec(1):0.25:EbN0vec(end); % Interpolation values
berfit(EbN0vec,ber,fitEbN0);
hold on;
for jj=1:numEbN0
    semilogy([EbN0vec(jj) EbN0vec(jj)],intv{jj},'g-+');
end
hold off;

参考

アプリ

• Bit Error Rate Analysis

関数

• berawgn | bercoding | berconfint | berfading | berfit | bersync

関連するトピック

• Analyze Performance with Bit Error Rate Analysis App
• BER 解析で使用される解析的表現