loss

判別分析分類器の分類損失

構文

L = loss(Mdl,Tbl,ResponseVarName)

L = loss(Mdl,Tbl,Y)

L = loss(Mdl,X,Y)

L = loss(___,Name=Value)

説明

L = loss(Mdl,Tbl,ResponseVarName) は、分類損失を返します。これは、Tbl.ResponseVarName 内の真のクラス ラベルと比較して、学習済みの判別分析分類器 Mdl が table Tbl 内の予測子データをどの程度の精度で分類するかを表すスカラーです。

分類損失 (L) は汎化または再代入の品質に対する尺度です。解釈は損失関数と加重スキームによって異なりますが、一般に、優れた分類器の方が分類損失値が小さくなります。

loss は、L を計算するときに、Mdl の Prior プロパティに格納されている、学習に使用されたクラス確率に対して、Tbl.ResponseVarName のクラス確率を正規化します。

L = loss(Mdl,Tbl,Y) は、table Tbl 内の予測子データと Y 内のクラス ラベルを使用して、分類器 Mdl の分類損失を返します。

L = loss(Mdl,X,Y) は、予測子データ X と Y 内の対応するクラス ラベルを使用して、学習済み判別分析分類器 Mdl の分類損失を返します。

L = loss(___,Name=Value) では、前の構文におけるいずれかの入力引数の組み合わせに加えて、1 つ以上の名前と値の引数を使用して追加オプションを指定します。たとえば、分類損失関数や観測値の重みを指定できます。

メモ

予測子データ X に欠損値があり、LossFun が "mincost" または "classiferror" に設定されていない場合、関数 loss で NaN が返されることがあります。詳細については、欠損値がある予測子データに対して loss で NaN が返されることがあるを参照してください。

例

分類誤差の推定

フィッシャーのアヤメのデータ セットを読み込みます。

load fisheriris

データ内の観測値をすべて使用して、判別分析モデルに学習をさせます。

Mdl = fitcdiscr(meas,species);

学習観測値を使用してモデルの分類誤差を推定します。

L = loss(Mdl,meas,species)

L = 
0.0200

または、Mdl がコンパクトでない場合は、Mdl を resubLoss に渡すことにより学習標本の分類誤差を推定できます。

入力引数

Mdl — 学習済みの判別分析分類器

ClassificationDiscriminant モデル オブジェクト | CompactClassificationDiscriminant モデル オブジェクト

学習済みの判別分析分類器。fitcdiscr で学習させた ClassificationDiscriminant モデル オブジェクト、または compact で作成した CompactClassificationDiscriminant モデル オブジェクトとして指定します。

Tbl — 標本データ

table

モデルを学習させるために使用する標本データ。table として指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。カテゴリカル予測子変数はサポートされていません。必要に応じて、応答変数 (カテゴリカルにすることが可能) 用および観測値の重み用の追加列を Tbl に含めることができます。Tbl には、Mdl に学習させるために使用したすべての予測子変数が含まれていなければなりません。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

Mdl を学習させるために使用した応答変数が Tbl に含まれている場合、ResponseVarName または Y を指定する必要はありません。

table に格納されている標本データを使用して Mdl に学習をさせた場合、loss の入力データも table に含まれていなければなりません。

データ型: table

ResponseVarName — 応答変数名

Tbl 内の変数の名前

応答変数の名前。Tbl 内の変数の名前で指定します。Mdl を学習させるために使用した応答変数が Tbl に含まれている場合、ResponseVarName を指定する必要はありません。

ResponseVarName には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、応答変数 Y が Tbl.Y として格納されている場合、"Y" として指定します。それ以外の場合、Tbl の列は Y を含めてすべて予測子として扱われます。

応答変数は、categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列でなければなりません。応答変数が文字配列の場合、各要素は配列の 1 つの行に対応しなければなりません。

データ型: char | string

X — 予測子データ

数値行列

予測子データ。数値行列として指定します。X の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。カテゴリカル予測子変数はサポートされていません。X の列内の変数は、Mdl の学習に使用した変数と同じでなければなりません。X の行数は Y の行数と等しくなければなりません。

行列に格納されている標本データを使用して Mdl に学習させた場合、loss の入力データも行列でなければなりません。

データ型: single | double

Y — クラス ラベル

categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

クラス ラベル。categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列を指定します。Y のデータ型は、Mdl の学習に使用した応答データと同じでなければなりません。(string 配列は文字ベクトルの cell 配列として扱われます)。

Y の長さは、Tbl または X の行数と等しくなければなりません。

データ型: categorical | char | string | logical | single | double | cell

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: L = loss(Mdl,meas,species,LossFun="binodeviance")

LossFun — 損失関数

"mincost" (既定値) | "binodeviance" | "classifcost" | "classiferror" | "exponential" | "hinge" | "logit" | "quadratic" | 関数ハンドル

損失関数。組み込みの損失関数名または関数ハンドルを指定します。

次の表に、組み込みの損失関数の値を示します。対応する文字ベクトルまたは string スカラーを使用して、いずれかを指定します。

値	説明
"binodeviance"	二項分布からの逸脱度
"classifcost"	観測誤分類コスト
"classiferror"	10 進数の誤分類率
"exponential"	指数損失
"hinge"	ヒンジ損失
"logit"	ロジスティック損失
"mincost"	最小予測誤分類コスト (事後確率である分類スコアの場合)
"quadratic"	二次損失

"mincost" は、事後確率である分類スコアに適しています。既定では、判別分析分類器は分類スコアとして事後確率を返します (predict を参照)。

関数ハンドル表記を使用して独自の関数を指定します。n は X 内の観測値の個数、K は異なるクラスの個数 (numel(Mdl.ClassNames)) であるとします。使用する関数のシグネチャは次のようになっていなければなりません。

lossvalue = lossfun(C,S,W,Cost)

ここで

• 出力引数 lossvalue はスカラーです。

• 関数名 (lossfun) を指定します。

• C は n 行 K 列の logical 行列であり、対応する観測値が属するクラスを各行が示します。列の順序は Mdl.ClassNames のクラスの順序に対応します。

  各行について観測値 p がクラス q に属する場合は C(p,q) = 1 を設定することにより、C を作成します。行 p の他のすべての要素を 0 に設定します。

• S は、分類スコアの n 行 K 列の行列です。列の順序は Mdl.ClassNames のクラスの順序に対応します。S は分類スコアの行列で、predict の出力と同様です。

• W は、観測値の重みの n 行 1 列の数値ベクトルです。W を渡す場合、重みは合計が 1 になるように正規化されます。

• Cost は、誤分類コストの、K 行 K 列の数値行列です。たとえば、Cost = ones(K) - eye(K) は、正しい分類のコストとして 0 を、誤分類のコストとして 1 を指定します。

例: LossFun="binodeviance"

例: LossFun=@Lossfun

データ型: char | string | function_handle

Weights — 観測値の重み

ones(size(X,1),1) (既定値) | 数値ベクトル | Tbl 内の変数の名前

観測値の重み。数値ベクトルまたは Tbl 内の変数の名前を指定します。X または Tbl の各行に含まれている観測値には、Weights の対応する重みが適用されます。

数値ベクトルで Weights を指定する場合、Weights のサイズは X または Tbl の行数と等しくなければなりません。

Tbl 内の変数名を Weights として指定する場合、文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、重みが Tbl.W として格納されている場合、Weights を "W" として指定します。それ以外の場合、Tbl の列は Tbl.W を含めてすべて予測子として扱われます。

独自の損失関数を指定しない場合、Weights が正規化され、合計が各クラスの事前確率の値になります。

例: Weights="W"

データ型: single | double | char | string

詳細

分類損失

"分類損失" 関数は分類モデルの予測誤差を評価します。複数のモデルで同じタイプの損失を比較した場合、損失が低い方が予測モデルとして優れていることになります。

以下のシナリオを考えます。

• L は加重平均分類損失です。

• n は標本サイズです。

• バイナリ分類は以下です。

  • y_j は観測されたクラス ラベルです。陰性クラスを示す -1 または陽性クラスを示す 1 (あるいは、ClassNames プロパティの最初のクラスを示す -1 または 2 番目のクラスを示す 1) を使用して符号化されます。

  • f(X_j) は予測子データ X の観測値 (行) j に対する陽性クラスの分類スコアです。

  • m_j = y_jf(X_j) は、y_j に対応するクラスに観測値 j を分類する分類スコアです。正の値の m_j は正しい分類を示しており、平均損失に対する寄与は大きくありません。負の値の m_j は正しくない分類を示しており、平均損失に大きく寄与します。

• マルチクラス分類 (つまり、K ≥ 3) をサポートするアルゴリズムの場合、次のようになります。

  • y_j^* は、K - 1 個の 0 と、観測された真のクラス y_j に対応する位置の 1 から構成されるベクトルです。たとえば、2 番目の観測値の真のクラスが 3 番目のクラスであり K = 4 の場合、y₂^* = [0 0 1 0]′ になります。クラスの順序は入力モデルの ClassNames プロパティ内の順序に対応します。

  • f(X_j) は予測子データ X の観測値 j に対するクラス スコアのベクトルで、長さは K です。スコアの順序は入力モデルの ClassNames プロパティ内のクラスの順序に対応します。

  • m_j = y_j^*′f(X_j).したがって m_j は、観測された真のクラスについてモデルが予測するスカラー分類スコアです。

• 観測値 j の重みは w_j です。観測値の重みは、その合計が Prior プロパティに格納された対応するクラスの事前確率になるように正規化されます。そのため、次のようになります。

  $${\displaystyle \sum _{j=1}^n{w}_j}=1.$$

この状況では、名前と値の引数 LossFun を使用して指定できる、サポートされる損失関数は次の表のようになります。

損失関数	LossFun の値	式
二項分布からの逸脱度	"binodeviance"	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left\{1+\exp \left[-2m_j\right]\right\}}.$$
観測誤分類コスト	"classifcost"	$$L={\displaystyle \sum _{j=1}^n{w}_j}{c}_{y_j{\widehat{y}}_j},$$ ここで、$${\widehat{y}}_j$$ はスコアが最大のクラスに対応するクラス ラベル、$$c_{y_j{\widehat{y}}_j}$$ は真のクラスが yj である場合に観測値をクラス $${\widehat{y}}_j$$ に分類するユーザー指定のコストです。
10 進数の誤分類率	"classiferror"	$$L={\displaystyle \sum _{j=1}^n{w}_j}I\left\{{\widehat{y}}_j\ne y_j\right\},$$ ここで、I{·} はインジケーター関数です。
クロスエントロピー損失	"crossentropy"	"crossentropy" はニューラル ネットワーク モデルのみに適しています。 加重クロスエントロピー損失は次となります。 $$L=-{\displaystyle \sum _{j=1}^n\frac{{\tilde{w}}_j\log (m_j)}{Kn}},$$ ここで重み $${\tilde{w}}_j$$ は、合計が 1 ではなく n になるように正規化されます。
指数損失	"exponential"	$$L={\displaystyle \sum _{j=1}^n{w}_j\exp \left(-m_j\right)}.$$
ヒンジ損失	"hinge"	$$L={\displaystyle \sum }_{j=1}^n{w}_j\max \left\{0,1-m_j\right\}.$$
ロジスティック損失	"logit"	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left(1+\exp \left(-m_j\right)\right)}.$$
最小予測誤分類コスト	"mincost"	"mincost" は、分類スコアが事後確率の場合にのみ適しています。 重み付きの最小予測分類コストは、次の手順を観測値 j = 1、...、n について使用することにより計算されます。 観測値 Xj をクラス k に分類する予測誤分類コストを推定します。 $${\gamma }_{jk}={\left(f{\left(X_j\right)}^{\prime }C\right)}_k.$$ f(Xj) は観測値 Xj のクラス事後確率の列ベクトルです。C はモデルの Cost プロパティに格納されるコスト行列です。 最小予測誤分類コストに対応するクラス ラベルを観測値 j について予測します。 $${\widehat{y}}_j=\underset{k=1,\mathrm{...},K}{\text{argmin}}{\gamma }_{jk}.$$ C を使用して、予測を行うために必要なコスト (cj) を求めます。 最小予測誤分類コスト損失の加重平均は次となります。 $$L={\displaystyle \sum _{j=1}^n{w}_j{c}_j}.$$
二次損失	"quadratic"	$$L={\displaystyle \sum _{j=1}^n{w}_j{\left(1-m_j\right)}^2}.$$

既定のコスト行列 (正しい分類の場合の要素値は 0、誤った分類の場合の要素値は 1) を使用する場合、"classifcost"、"classiferror"、および "mincost" の損失の値は同じです。既定以外のコスト行列をもつモデルでは、ほとんどの場合は "classifcost" の損失と "mincost" の損失が等価になります。これらの損失が異なる値になる可能性があるのは、最大の事後確率をもつクラスへの予測と最小の予測コストをもつクラスへの予測が異なる場合です。"mincost" は分類スコアが事後確率の場合にしか適さないことに注意してください。

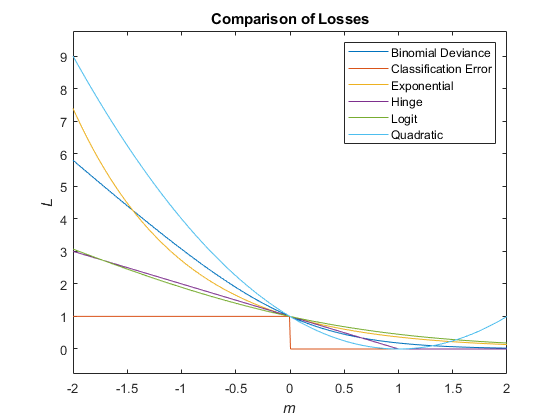
次の図では、1 つの観測値のスコア m に対する損失関数 ("classifcost"、"crossentropy"、および "mincost" を除く) を比較しています。いくつかの関数は、点 (0,1) を通過するように正規化されています。

事後確率

点 x がクラス k に属する事後確率は、事前確率と多変量正規密度の積です。1 行 d 列の平均 μ_k および 1 行 d 列の点 x における d 行 d 列の共分散 Σ_k をもつ、多変量正規密度関数は次のとおりです。

$$P\left(x|k\right)=\frac{1}{{\left({\left(2\pi \right)}^d\left|{\Sigma }_k\right|\right)}^{1/2}}\exp \left(-\frac{1}{2}\left(x-{\mu }_k\right){\Sigma }_k^{-1}{\left(x-{\mu }_k\right)}^T\right),$$

ここで、$$\left|{\Sigma }_k\right|$$ は Σ_k の行列式、$${\Sigma }_k^{-1}$$ は逆行列です。

P(k) でクラス k の事前確率を表してみます。すると、観測 x がクラス k になる事後確率は次のとおりです。

$$\widehat{P}\left(k|x\right)=\frac{P\left(x|k\right)P\left(k\right)}{P\left(x\right)},$$

ここで P(x) は正規化定数、P(x|k)P(k) の合計 k です。

事前確率

事前確率は次の 3 つの選択肢のいずれかです。

• 'uniform' — クラス k の事前確率は、クラスの総数に対して 1 です。

• 'empirical' — クラス k の事前確率は、クラス k の学習標本の数を学習標本の合計で除算した値です。

• カスタム — クラス k の事前確率は、prior ベクトルの k 番目の要素です。fitcdiscr を参照してください。

分類モデル (Mdl) を作成した後で、ドット表記を使用して事前確率を設定できます。

Mdl.Prior = v;

ここで v は各要素が発生する頻度を表す正の要素のベクトルです。新しい事前確率を設定する場合に、分類器に再学習させる必要はありません。

コスト

観測ごとの予測コストの行列は、コストで定義されています。

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

この関数は、tall 配列を完全にサポートします。この関数でインメモリ データまたは tall データに対して学習を行ったモデルを使用できます。

詳細は、tall 配列を参照してください。

バージョン履歴

R2011b で導入

R2022a: 欠損値がある予測子データに対して loss で NaN が返されることがある

関数 loss で加重平均分類損失を計算する際に、スコアが NaN の観測値が省略されなくなりました。そのため、予測子データ X に欠損値があり、名前と値の引数 LossFun が "classifcost"、"classiferror"、または "mincost" として指定されていない場合に、loss で NaN が返されることがあります。ほとんどの場合、テスト セットの観測値に予測子の欠損がなければ、関数 loss で NaN が返されることはありません。

この変更により、fitcauto を使用する場合の分類モデルの自動選択が改善されます。この変更の前は、NaN 以外の予測子が少ないモデルが選択される (新しいデータの分類に最適であると予測される) ことがありました。

コードの loss で NaN が返される場合、このような結果にならないように、次のいずれかを行ってコードを更新できます。

• rmmissing または fillmissing を使用して、欠損値を削除するか置き換えます。

• 名前と値の引数 LossFun を "classifcost"、"classiferror"、または "mincost" として指定します。

次の表に、オブジェクト関数 loss で NaN が返される可能性がある分類モデルを示します。詳細については、それぞれの関数 loss の「互換性の考慮事項」を参照してください。

モデル タイプ	完全またはコンパクトなモデル オブジェクト	オブジェクト関数 loss
判別分析分類モデル	ClassificationDiscriminant, CompactClassificationDiscriminant	loss
分類用のアンサンブル学習器	ClassificationEnsemble, CompactClassificationEnsemble	loss
ガウス カーネル分類モデル	ClassificationKernel	loss
k 最近傍分類モデル	ClassificationKNN	loss
線形分類モデル	ClassificationLinear	loss
ニューラル ネットワーク分類モデル	ClassificationNeuralNetwork, CompactClassificationNeuralNetwork	loss
サポート ベクター マシン (SVM) 分類モデル	ClassificationSVM, CompactClassificationSVM	loss

参考

クラス

• ClassificationDiscriminant | CompactClassificationDiscriminant

関数

• fitcdiscr | edge | margin | predict

トピック

• 判別分析による分類