データを表面として表す

データ グリッドをプロットする関数

MATLAB^® のグラフでは、x-y 座標平面に引かれた四角形のグリッドの上方にある点の z 座標によって表面の位置が決まります。プロットは、隣り合った点を直線で結ぶことによって作成されます。表面プロットは、数値書式で表示するには大きすぎる行列を可視化したり、2 変数の関数をグラフ化するのに有効です。

MATLAB は、さまざまな表面プロットを作成できます。メッシュ プロットは、定義した点を結ぶラインのみを色付けしたワイヤーフレーム表面です。表面プロットは、ラインと表面を合わせたもので、色で表示されます。次の表は、さまざまな形式を示しています。

関数	用途
mesh, surf	表面プロット
meshc, surfc	等高線図が下にある表面プロット
meshz	カーテン プロット (基準平面) をもつ表面プロット
pcolor	平面プロット (値が色のみに比例する)
surfl	指定した方向からライティングされた表面プロット
surface	表面グラフィックス オブジェクトを作成するための低水準関数 (高水準関数のベース)

データのグリッド化と内挿のための関数

データを表面として表せるようにデータの再構成と内挿が必要な場合は、以下の関数が役立ちます。

関数	用途
meshgrid	2 次元および 3 次元の空間の四角形グリッド
griddata	内挿散布データ
griddedInterpolant	グリッド データの内挿
scatteredInterpolant	内挿散布データ

データの内挿方法は、グリッド データの内挿および散布データの内挿を参照してください。

メッシュ プロットと表面プロット

mesh コマンドと surf コマンドは、行列データの 3 次元表面プロットを作成します。Z が行列で、その要素 Z(i,j) がグリッド (i,j) 上の表面の高さを定義している場合、

mesh(Z)

は、表面の色付きのワイヤーフレーム ビューを作成し、3 次元で表示します。同様に、

surf(Z)

は、表面の色付き、塗りつぶし付きのビューを作成し、3 次元で表示します。通常、小平面は四辺形でそれぞれが決まった色を持ち、黒で縁取りされています。しかし、コマンド shading により、メッシュラインの消去 (shading flat)、もしくはその小平面に内挿されたシェーディングの選択 (shading interp) のいずれかが可能になります。

surface オブジェクト プロパティは、表面の可視状態に関する付加的なコントロールを与えます。ユーザーは、エッジ ライン スタイル、頂点のマーカー、面の色付け、ライティング特性等を選択することができます。

2 変数関数の可視化

1. 2 変数の関数、z = f (x,y) を表示するには、関数の定義域でそれぞれ行と列が繰り返される行列 X と Y を生成します。これらの行列を使用して関数の値を求め、グラフを作成します。

2. 関数 meshgrid は、2 つのベクトル x と y で指定された定義域を行列 X と Y に変換します。次に、これらの行列を使用して 2 変数関数の値を求めます。X の行はベクトル x のコピーで、Y の列はベクトル y のコピーです。

例1 例: 関数 meshgrid の使用

meshgrid の使用方法を示すため、関数 sin(r)/r または関数 sinc について考えます。この関数を x と y について、共に -8 ～ 8 の範囲で、関数計算するために、ユーザーは 1 つのベクトル引数のみを meshgrid に渡す必要があります。

[X,Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 + Y.^2) + eps;

行列 R は、行列の中心、すなわち原点からの距離です。eps を追加することで、(次のステップで) ゼロ除算によってデータ内に Inf 値が生成されるのを防ぎます。

関数 sinc を作成し、mesh で Z をプロットしたものが 3 次元表面になります。

Z = sin(R)./R;
figure
mesh(X,Y,Z)

隠されたラインの削除

既定の設定では、MATLAB はメッシュ プロット内で視点から隠れるラインを削除します。これはプロット面が塗りつぶしされていない場合でも削除します。ラインの削除を行わない場合や、メッシュ プロットの面を透明にするには、hidden コマンドを使用します。

hidden off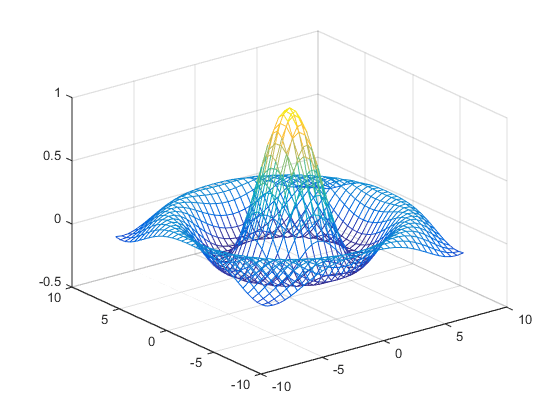

表面の形状の強調

MATLAB は、ユーザーのグラフの情報を強調するさまざまな技法を提供しています。たとえば、関数 sinc のグラフは、前のグラフと同じデータを使用していますが、ライティングとビューの調整と異なるカラーマップを使用して、グラフ化された関数 (daspect、axis、view、camlight) の形状を強調することができます。

figure
colormap hsv
surf(X,Y,Z,'FaceColor','interp',...
   'EdgeColor','none',...
   'FaceLighting','gouraud')
daspect([5 5 1])
axis tight
view(-50,30)
camlight left

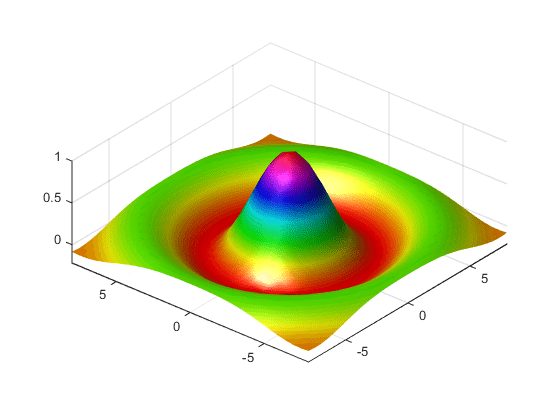
表面プロットの詳細については、関数 surf を参照してください。

等間隔にサンプリングされていないデータの表面プロット

meshgrid を使用して、等間隔にサンプリングされたデータ点のグリッドを作成し、関数 sinc を計算し、グラフ化します。そして、MATLAB は隣り合った行列要素を結合することにより、表面プロットを作成し、四辺形のメッシュを作成します。

等間隔にサンプリングされていないデータから表面プロットを作成するには、まず scatteredInterpolant を使用して、等間隔になるように値を内挿し、その後通常どおりに mesh と surf を使用します。

例 - 一様でないデータを表面に表示する

この例では、指定した範囲のランダムな点で関数 sinc を計算し、表面プロットとして表示するための等間隔にサンプルされたデータを作成します。このプロセスは、以下の手順を含んでいます。

• linspace を使用して、一様に分布していないサンプル データの占める範囲に対して、等間隔に分布する値を作成します。

• meshgrid を使用して、linspace の出力をベースにプロットに必要なグリッドを作成します。

• scatteredInterpolant を使用して、不規則にサンプリングされたデータにデータを内挿して、meshgrid で出力される等間隔のグリッドを作成します。

• プロット関数を使用して、データを表示します。

1. まず、[-8, 8] の範囲で不規則にサンプリングされたデータを作成し、このデータを使用して関数の値を求めます。

   x = rand(100,1)*16 - 8;
   y = rand(100,1)*16 - 8;
   r = sqrt(x.^2 + y.^2) + eps;
   z = sin(r)./r;
   

2. 関数 linspace は、必要な要素数の等間隔データを作成する便利な方法です。次のステートメントは、上記の関数 sinc の例で -8:.5:8 を指定した場合と同じ解像度で、乱数データの範囲を占めるベクトルを作成します。

   xlin = linspace(min(x),max(x),33);
   ylin = linspace(min(y),max(y),33);
   

3. 次に、これらの点を使用して、等間隔のグリッドを作成します。

   [X,Y] = meshgrid(xlin,ylin);
   

4. このプロセスのキーは、元のデータ点 (この例ではランダム データ) での関数値を基に、scatteredInterpolant を使用して等間隔の点に関数値を内挿することです。次のステートメントは、新しいデータ点を作成するために、既定の線形内挿を行います。

   f = scatteredInterpolant(x,y,z);
   Z = f(X,Y);

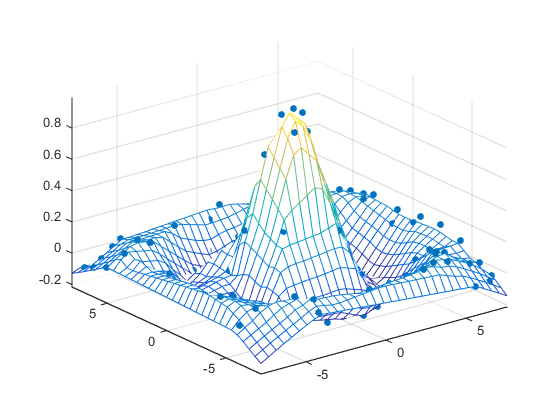
5. 内挿されたデータと一様でないデータをプロットします。

   figure
   mesh(X,Y,Z) %interpolated
   axis tight; hold on
   plot3(x,y,z,'.','MarkerSize',15) %nonuniform
   

   

データの形状の変更

次のような 3 要素 (X, Y, Z) をもつデータの集合体があるとします。

X	Y	Z
1	1	152
2	1	89
3	1	100
4	1	100
5	1	100
1	2	103
2	2	0
3	2	100
4	2	100
5	2	100
1	3	89
2	3	13
3	3	100
4	3	100
5	3	100
1	4	115
2	4	100
3	4	187
4	4	200
5	4	111
1	5	100
2	5	85
3	5	111
4	5	97
5	5	48

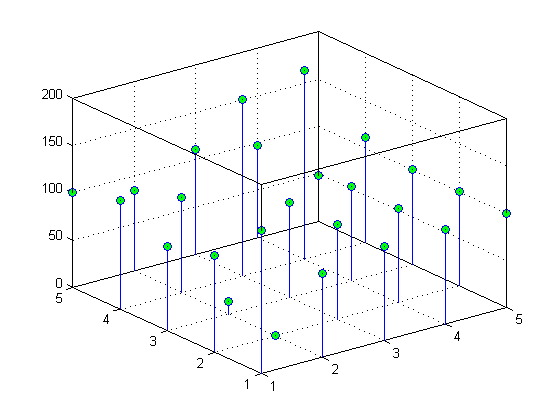
surf、contour、stem3 などのさまざまな MATLAB グラフ タイプを使用すると、データをベクトル形式で表すことができます。これを行うには、まずデータを再構成します。(X, Y) の値を使用して、Z 値が含まれる xy 平面の座標を定義します。関数 reshape および transpose を使用すると、3 つの要素 (X, Y, Z) によって四角形グリッドが作成されるようにデータを再構成できます。

x = reshape(X,5,5)';
y = reshape(Y,5,5)';
z = reshape(Z,5,5)';

形状の変更によって、5 行 5 列の配列が 3 つ得られます。

x =

     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5

y =

     1     1     1     1     1
     2     2     2     2     2
     3     3     3     3     3
     4     4     4     4     4
     5     5     5     5     5

z =

   152    89   100   100   100
   103     0   100   100   100
    89    13   100   100   100
   115   100   187   200   111
   100    85   111    97    48

これで X と Y に対する Z の値を表すことができます。たとえば、以下のように 3 次元ステム グラフを作成できます。

stem3(x,y,z,'MarkerFaceColor','g')

パラメトリックな表面

表面を描画する関数は、2 つの付加的なベクトルまたは行列引数を使用して、指定した x と y のデータで表面を記述します。Z が m 行 n 列の行列で、x は長さ n のベクトルで、y は長さ m のベクトルの場合、

mesh(x,y,Z,C)

は、次の点で頂点が色 C(i,j) であるメッシュ表面を記述しています。

(x(j), y(i), Z(i,j))

ここで、x は Z の列で、y はその行に対応します。

より一般的に、X Y Zおよび C が同じ次元の行列の場合、

mesh(X,Y,Z,C)

は、次の点で頂点が色 C(i,j) であるメッシュ表面を記述しています。

(X(i,j), Y(i,j), Z(i,j))

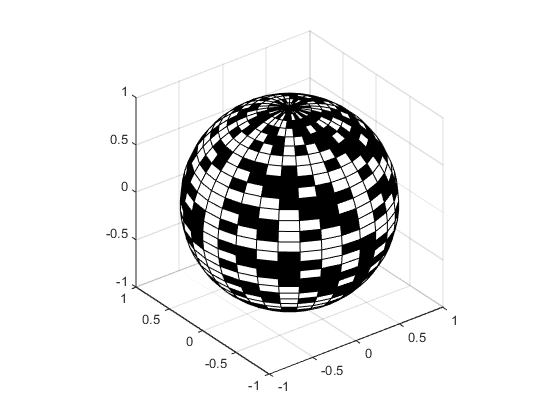
この例は、球面座標を使用して球面を描き、信号処理のエンコード理論で使われる直交行列、アダマール行列内のプラスとマイナスのパターンを使用して、この球面を色付けします。ベクトルの theta と phi は、-π ≤ theta ≤ π と -π/2 ≤ phi ≤ π/2 の範囲です。theta が行ベクトル、phi が列ベクトルなので、行列 X, Y, Z を作成する乗算は、ベクトルの外積になります。

figure
k = 5;
n = 2^k-1;
theta = pi*(-n:2:n)/n;
phi = (pi/2)*(-n:2:n)'/n;
X = cos(phi)*cos(theta);
Y = cos(phi)*sin(theta);
Z = sin(phi)*ones(size(theta));
colormap([0 0 0;1 1 1])
C = hadamard(2^k); 
surf(X,Y,Z,C)
axis square