このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

n4sid

時間領域または周波数領域のデータを使用した部分空間法による状態空間モデルの推定

構文

sys = n4sid(tt,nx)

sys = n4sid(u,y,nx,'Ts',Ts)

sys = n4sid(data,nx)

sys = n4sid(___,Name,Value)

sys = n4sid(___,opt)

[sys,x0] = n4sid(___)

説明

状態空間モデルの推定

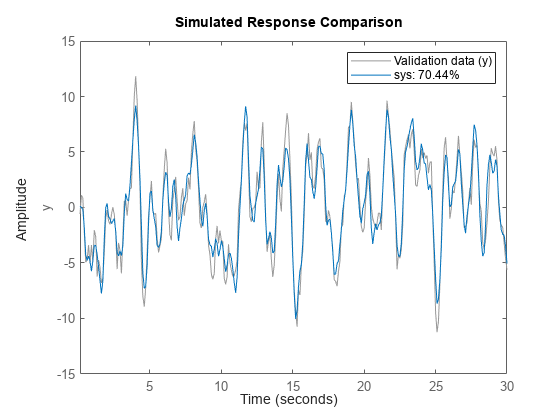
sys = n4sid(tt,nx) は、timetable tt のすべての入力信号と出力信号を使用して、次数 nx の離散時間状態空間モデル sys を推定します。

sys は次の形式のモデルです。

$$\begin{array}{l}\dot{x}(t)=Ax(t)+Bu(t)+Ke(t)\\ y(t)=Cx(t)+Du(t)+e(t)\end{array}$$

A、B、C、D、および K は状態空間行列です。u(t) は入力、y(t) は出力、e(t) は外乱、x(t) は nx 個の状態のベクトルです。

A、B、C、および K のエントリは、既定ではすべて推定可能な自由パラメーターです。動的システムの場合、D は既定ではゼロに固定されます。これは、システムに直達がないことを意味します。静的システム (nx = 0) の場合、D は既定では推定可能なパラメーターです。

この構文は SISO および MISO システムに使用できます。この関数では、timetable の最後の変数は単一の出力信号であると仮定します。この構文を使用して、tt に唯一の出力を表す単一の変数が含まれる場合に時系列モデルを推定することもできます。

MIMO システムの場合や、推定に使用する予定の変数よりも多くの変数が含まれる timetable の場合、名前と値の引数を使用して、必要な入力チャネルと出力チャネルの名前を指定する必要もあります。詳細については、tt を参照してください。

連続時間モデルを推定するには、名前と値の構文を使用して 'Ts' を 0 に設定します。

sys = n4sid(u,y,nx,'Ts',Ts) は、コンマ区切りの行列 u,y 内の時間領域入力信号と出力信号およびサンプル時間 Ts を使用します。この構文は SISO、MISO、および MIMO システムに使用できます。

行列ベースのデータから連続時間モデルを推定することは推奨されません。

sys = n4sid(data,nx) は、データ オブジェクト data 内の時間領域データまたは周波数領域データを使用します。この構文は特に、周波数領域データまたは周波数応答データを使用して状態空間モデルを推定する場合、またはデータ オブジェクトが提供する追加情報 (データのサンプル時間や実験のラベル付けなど) を利用する場合に使用します。

追加のオプションの指定

sys = n4sid(___,Name,Value) は、1 つ以上の名前と値のペアの引数で指定された追加のオプションを組み込みます。たとえば、連続時間モデルを推定するには、サンプル時間 'Ts' を 0 と指定します。A、B、C、D、および K の各行列の既定の動作を変更するには、名前と値のペアの引数 'Form'、'Feedthrough'、'DisturbanceModel' を使用します。

この構文は、前述の任意の入力引数の組み合わせで使用できます。

sys = n4sid(___,opt) は、推定オプション opt を指定します。これらのオプションには、初期状態、推定の目的、推定に使用する部分空間アルゴリズムに関する選択が含まれます。opt は、前述の任意の入力引数の組み合わせの後に指定します。

推定された初期状態を返す

[sys,x0] = n4sid(___) は、推定時に計算された初期状態の値を返します。この構文では、前述の任意の入力引数の組み合わせで使用できます。

例

状態空間モデル

状態空間モデルを推定し、その応答を測定出力と比較します。

timetable に格納されている入出力データ tt1 を読み込みます。

load sdata1.mat tt1

4 次状態空間モデルを推定します。

nx = 4;
sys = n4sid(tt1,nx)

sys =
  Discrete-time identified state-space model:
    x(t+Ts) = A x(t) + B u(t) + K e(t)
       y(t) = C x(t) + D u(t) + e(t)
 
  A = 
              x1         x2         x3         x4
   x1     0.8392    -0.3129    0.02105    0.03743
   x2     0.4768     0.6671     0.1428   0.003757
   x3   -0.01951    0.08374   -0.09761      1.046
   x4  -0.003885   -0.02914    -0.8796   -0.03171
 
  B = 
               u
   x1    0.02635
   x2   -0.03301
   x3  7.256e-05
   x4  0.0005861
 
  C = 
           x1       x2       x3       x4
   y    69.08    26.64   -2.237  -0.5601
 
  D = 
      u
   y  0
 
  K = 
               y
   x1   0.003282
   x2   0.009339
   x3  -0.003232
   x4   0.003809
 
Sample time: 0.1 seconds

Parameterization:
   FREE form (all coefficients in A, B, C free).
   Feedthrough: none
   Disturbance component: estimate
   Number of free coefficients: 28
   Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.

Status:                                          
Estimated using N4SID on time domain data "tt1". 
Fit to estimation data: 76.33% (prediction focus)
FPE: 1.21, MSE: 1.087                            
 

シミュレートしたモデルの応答を測定出力と比較します。

compare(tt1,sys)

プロットから、シミュレートしたモデルと推定データの間の適合率が 70% を超えていることがわかります。

推定に関する詳しい情報は、idss の sys.Report プロパティを調べて確認できます。

sys.Report

ans = 
          Status: 'Estimated using N4SID with prediction focus'
          Method: 'N4SID'
    InitialState: 'estimate'
        N4Weight: 'CVA'
       N4Horizon: [6 10 10]
             Fit: [1x1 struct]
      Parameters: [1x1 struct]
     OptionsUsed: [1x1 idoptions.n4sid]
       RandState: [1x1 struct]
        DataUsed: [1x1 struct]

たとえば、推定された初期状態に関する詳しい情報を調べます。

sys.Report.Parameters.X0

ans = 4×1

   -0.0085
    0.0052
   -0.0193
    0.0282

推定による最適なモデル次数の特定

iddata オブジェクトに格納されている入出力データ z1 を読み込みます。

load iddata1 z1

引数 nx を 1 から 10 までの範囲に指定して、最適なモデル次数を調べます。

nx = 1:10;
sys = n4sid(z1,nx);

自動生成されるプロットに、nx で指定した次数のモデルに対するハンケル特異値が表示されます。

ハンケル特異値が比較的小さい状態については破棄してかまいません。提案される既定の次数の選択は 2 です。

[選択した次数] のリストでモデル次数を選択し、[適用] をクリックします。

推定オプションの指定

推定データを読み込みます。

load iddata2 z2

推定オプションを指定します。重み付けスキーム 'N4Weight' を 'SSARX' に設定し、推定ステータス表示オプション 'Display' を 'on' に設定します。

opt = n4sidOptions('N4Weight','SSARX','Display','on')

Option set for the n4sid command:

          InitialState: 'estimate'
              N4Weight: 'SSARX'
             N4Horizon: 'auto'
               Display: 'on'
      InputInterSample: 'auto'
           InputOffset: []
          OutputOffset: []
    EstimateCovariance: 1
          OutputWeight: []
                 Focus: 'prediction'
       WeightingFilter: []
      EnforceStability: 0
              Advanced: [1x1 struct]

更新したオプション セットを使用して、3 次状態空間モデルを推定します。

nx = 3;
sys = n4sid(z2,nx,opt);

形式、直達、外乱モデルの行列の変更

A、B、および C の各行列の正準形を変更し、D 行列に直達項を含め、K 行列の外乱モデルの推定を排除します。

入出力データを読み込み、n4sid の既定のオプションを使用して 4 次システムを推定します。

load iddata1 z1
sys1 = n4sid(z1,4);

モード形式を指定し、A 行列を既定の A 行列と比較します。

sys2 = n4sid(z1,4,'Form','modal');
A1 = sys1.A

A1 = 4×4

    0.8392   -0.3129    0.0211    0.0374
    0.4768    0.6671    0.1428    0.0038
   -0.0195    0.0837   -0.0976    1.0462
   -0.0039   -0.0291   -0.8796   -0.0317

A2 = sys2.A

A2 = 4×4

    0.7554    0.3779         0         0
   -0.3779    0.7554         0         0
         0         0   -0.0669    0.9542
         0         0   -0.9542   -0.0669

直達項を含め、D 行列を比較します。

sys3 = n4sid(z1,4,'Feedthrough',1);
D1 = sys1.D

D1 = 0

D3 = sys3.D

D3 = 0.0487

外乱のモデル化を排除し、K 行列を比較します。

sys4 = n4sid(z1,4,'DisturbanceModel','none');
K1 = sys1.K

K1 = 4×1

    0.0033
    0.0093
   -0.0032
    0.0038

K4 = sys4.K

K4 = 4×1

     0
     0
     0
     0

連続時間正準形モデル

連続時間正準形モデルを推定します。

推定データを読み込みます。

load iddata1 z1

モデルを推定します。Ts を 0 に設定して連続モデルを指定します。

nx = 2;
sys = n4sid(z1,nx,'Ts',0,'Form','canonical');

sys は、正準形の 2 次連続時間状態空間モデルです。

閉ループ データからの状態空間モデルの推定

部分空間アルゴリズム SSARX を使用して閉ループ データから状態空間モデルを推定します。このアルゴリズムは、フィードバックの影響を取得するのに他の重み付けアルゴリズムよりも優れています。

ホワイト ノイズで破損した 2 次システムの閉ループ推定データを生成します。

N = 1000; 
K = 0.5;
rng('default');
w = randn(N,1);
z = zeros(N,1); 
u = zeros(N,1); 
y = zeros(N,1);
e = randn(N,1);
v = filter([1 0.5],[1 1.5 0.7],e);
for k = 3:N
   u(k-1) = -K*y(k-2) + w(k);
   u(k-1) = -K*y(k-1) + w(k);
   z(k) = 1.5*z(k-1) - 0.7*z(k-2) + u(k-1) + 0.5*u(k-2);
   y(k) = z(k) + 0.8*v(k);
end
dat = iddata(y, u, 1);

N4SID アルゴリズムで使用される重み付けスキーム 'N4weight' を指定します。2 つのオプション セットを作成します。一方のオプション セットで、'N4weight' を 'CVA' に設定します。もう一方のオプション セットで、'N4weight' を 'SSARX' に設定します。

optCVA = n4sidOptions('N4weight','CVA');
optSSARX = n4sidOptions('N4weight','SSARX');

オプション セットを使用して状態空間モデルを推定します。

sysCVA = n4sid(dat,2,optCVA);
sysSSARX = n4sid(dat,2,optSSARX);

2 つのモデルの推定データとの適合を比較します。

compare(dat,sysCVA,sysSSARX);

プロットからわかるように、SSARX アルゴリズムを使用して推定したモデルの方が CVA アルゴリズムを使用して推定したモデルよりも適合しています。

入力引数

tt — timetable ベースの推定データ

timetable | timetable の cell 配列。

入力チャネルと出力チャネルを表す変数を含んでいる等間隔サンプルの timetable として、または、複数実験データの場合は timetable の cell 配列として指定します。

timetable 全体の使用

tt 内のすべての変数を入力チャネルまたは出力チャネルとして使用し、一連の入力チャネル変数の後に一連の出力チャネル変数が続くように変数が構成されている場合、次のようになります。

• SISO システムの場合は、tt を N_s 行 2 列の timetable として指定します。N_s はサンプルの数で、2 つの timetable 変数はそれぞれ測定された入力チャネルと出力チャネルを表します。

• MIMO システムの場合、tt を N_s 行 (N_u+N_y) 列の timetable として指定します。N_u は入力の数、N_y は出力の数です。最初の N_u 個の変数には入力チャネルが含まれ、残りの N_y 個の変数には出力チャネルが含まれなければなりません。

  状態空間モデルまたは伝達関数モデルを推定している場合は、次の節で説明されているように、入力チャネルと出力チャネルも明示的に指定しなければなりません。

• 複数実験データの場合は、データを timetable の N_e 行 1 列の cell 配列として指定します。N_e は実験数です。すべての実験のサンプル時間が一致していなければなりません。

timetable から選択した変数の使用

使用可能なチャネルのサブセットのみを使用する場合、入力チャネルおよび出力チャネルの変数が混在している場合、MIMO 空間状態モデルまたは伝達関数モデルを推定している場合など、入力チャネルと出力チャネルを明示的に特定する場合は、'InputName' および 'OutputName' の名前と値の引数を使用して、入力および出力として使用する変数を指定します。

たとえば、tt に 6 つのチャネル変数 "u1"、"u2"、"u3"、および "y1"、"y2"、"y3" が含まれているとします。変数 "u1" と "u2" を入力、変数 "y1" と "y3" を出力として推定に使用します。推定を実行するには、次のコマンドを使用します。

sys = n4sid(tt,__,'InputName',["u1" "u2"],'OutputName',["y1" "y3"])

timetable を使用した時系列モデルの推定

入力/出力モデルではなく時系列モデルを推定する場合は、tt からの出力変数のみを使用します。必要な出力変数のみを含める tt を指定できます。または、tt に入力変数も含まれる場合は tt から出力変数を抽出できます。指定方法は、入力/出力モデルの推定の場合と似ています。

• 単出力システムの場合、tt を N_s 行 1 列の timetable として指定します。

• 多変量システムの場合、tt を N_s 行 (N_y) 列の timetable として指定します。tt 内のすべての変数を使用する予定である場合も、それらの変数が入力変数と解釈されないように、'OutputName' の名前と値の引数を使用してそれらの変数をすべて指定する必要があります。

使用する変数以外の変数 (入力変数、追加の出力変数など) も含まれる timetable tt の場合は、使用する出力変数を指定するのに加え、'InputName' に空の配列を指定します。

たとえば、tt に 6 つの変数 "u1"、"u2"、"u3"、および "y1"、"y2"、"y3" が含まれているとします。出力変数 "y3" および "y1" を時系列推定に使用します。推定を実行するには、次のコマンドを使用します。

sys = n4sid(tt,__,'OutputName',["y1" "y3"],'InputName',[])

推定データ型の取り扱いの詳細については、Data Domains and Data Types in System Identification Toolboxを参照してください。

u, y — 行列ベースの推定データ

行列 | 行列の cell 配列

推定データ。SISO システムの場合は、等間隔でサンプリングされた入力および出力時間領域信号値を含む、N_s 行 1 列の実数値行列のコンマ区切りのペアとして指定します。ここで、N_s はサンプルの数です。

MIMO システムの場合は、u,y を、以下の次元をもつ入力行列と出力行列のペアとして指定します。

• u — N_s 行 N_u 列の行列。N_u は入力の数です。

• y — N_s 行 N_y 列の行列。N_y は出力の数です。

複数実験データの場合は、u,y を 1 行 N_e 列の cell 配列のペアとして指定します。N_e は実験数です。すべての実験のサンプル時間が一致していなければなりません。

出力のみを含み、入力を含まない時系列データの場合は、y のみを指定します。

制限

• 行列ベースのデータは、周波数領域データからの推定をサポートしません。iddata オブジェクトや idfrd オブジェクトなどのデータ オブジェクト (data を参照) を使用する必要があります。

• 推定データはサンプル時間を提供しないため、連続時間推定では推定データに行列を使用することは推奨されません。データは 1 Hz でサンプリングされると仮定されます。連続時間推定の場合、各行列を timetable に変換することが推奨されます。たとえば、行列 um および ym をサンプル時間が 0.5 分の timetable tt に変換するには、次のコマンドを使用します。

  tt = timetable(um,ym,'rowtimes',minutes(0.5*(1:size(u,1))))

  行列ベースの SISO データを timetable に変換する詳細な例については、Convert SISO Matrix Data to Timetableを参照してください。MIMO 行列のペアを timetable に変換する例については、連続時間モデルを推定するために MIMO 行列データを timetable に変換を参照してください。

  推定データ型の取り扱いの詳細については、Data Domains and Data Types in System Identification Toolboxを参照してください。

data — 推定データ

iddata オブジェクト | frd オブジェクト | idfrd オブジェクト

推定データ。iddata オブジェクト、frd オブジェクト、または idfrd オブジェクトとして指定します。

時間領域の推定の場合、data は入力信号と出力信号の値を含む iddata オブジェクトでなければなりません。

周波数領域の推定の場合、data は次のいずれかになります。

• 記録された周波数応答データ (frd (Control System Toolbox) または idfrd)

• プロパティが次のように指定された iddata オブジェクト。

  • InputData — 入力信号のフーリエ変換

  • OutputData — 出力信号のフーリエ変換

  • Domain — 'Frequency'

推定データは等間隔サンプルでなければなりません。既定では、モデルのサンプル時間は推定データのサンプル時間に設定されます。

複数実験データの場合、すべての実験のサンプル時間とサンプル間動作が一致していなければなりません。

データの領域に応じて、推定できるモデルのタイプが決まります。

• 時間領域データまたは離散時間の周波数領域データ — 連続時間モデルと離散時間モデル

• 連続時間の周波数領域データ — 連続時間モデルのみ

nx — 推定モデルの次数

1:10 (既定値) | 正の整数スカラー | 正の整数ベクトル | best | 0

推定モデルの次数。非負の整数、または正の整数の範囲を含むベクトルとして指定します。

• 推定モデルの目的の次数が既にわかっている場合は、nx をスカラーとして指定します。

• 推定モデルの最も効果的な次数を選択するために可能性がある次数の範囲を比較する場合は、その範囲を nx に指定します。n4sid により、システムにおけるそれぞれの状態の相対的なエネルギーの寄与を示すハンケル特異値のプロットが作成されます。ハンケル特異値が比較的小さい状態は、モデルの精度にほとんど寄与せず、破棄しても影響はほとんどありません。維持する状態のうちで最も高い状態のインデックスがモデル次数になります。プロット ウィンドウには、使用する次数の提案も示されます。この提案を受け入れることも、別の次数を入力することもできます。例については、推定による最適なモデル次数の特定を参照してください。

  nx を指定しない場合、または nx を best と指定した場合、範囲 1:10 から nx が自動的に選択されます。

• 静的システムを同定する場合は、nx を 0 に設定します。

opt — 推定のオプション

n4sidOptions オプション セット

推定オプション。n4sidOptions オプション セットとして指定します。opt で指定するオプションには以下が含まれます。

• 推定の目的

• 初期条件の処理

• 部分空間アルゴリズムに関する選択

オプションを指定する方法の例については、推定オプションの指定および連続時間正準形モデルを参照してください。

名前と値の引数

引数のオプションのペアを Name1=Value1,...,NameN=ValueN として指定します。Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後に表示されなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: sys = n4sid(data,nx,'Form','modal')

Ts — 推定モデルのサンプル時間

データのサンプル時間 (data.Ts) (既定値) | 0 | 正のスカラー

推定モデルのサンプル時間。'Ts' と 0 または正のスカラーのいずれかで構成されるコンマ区切りのペアとして指定します。

• 連続時間モデルの場合、'Ts' を 0 と指定します。周波数領域では、連続時間の周波数領域データを使用すると連続時間モデルになります。

• 離散時間モデルの場合、'Ts' は TimeUnit プロパティに格納された単位でのデータのサンプル時間に設定されます。

InputDelay — 入力遅延

0 (既定値) | スカラー | ベクトル

各入力チャネルの入力遅延。'InputDelay' と数値ベクトルで構成されるコンマ区切りのペアとして指定します。

• 連続時間モデルの場合、TimeUnit プロパティに格納された時間単位で 'InputDelay' を指定します。

• 離散時間モデルの場合、サンプル時間 Ts の整数倍で 'InputDelay' を指定します。たとえば、'InputDelay' を 3 に設定すると、3 サンプリング周期の遅延が指定されます。

N_u 個の入力があるシステムの場合、InputDelay を N_u 行 1 列のベクトルに設定します。このベクトルの各エントリは、対応する入力チャネル用の入力遅延を表す数値です。

すべてのチャネルに同じ遅延を適用するには、'InputDelay' をスカラーとして指定します。

Form — 正準形のタイプ

'free' (既定値) | 'modal' | 'companion' | 'canonical'

sys の正準形のタイプ。'Form' と次の値のいずれかで構成されるコンマ区切りのペアとして指定します。

• 'free' — 行列 A、B、C、D、および K のすべてのエントリを自由なものとして扱います。

• 'modal' — sys をモード形式で取得します。

• 'companion' — sys をコンパニオン形式で取得します。

• 'canonical' — sys を可観測性の正準形で取得します。

正準形の定義については、状態空間実現を参照してください。

これらの形式を同定に使用する方法の詳細については、Estimate State-Space Models with Canonical Parameterizationを参照してください。

例については、形式、直達、外乱モデルの行列の変更を参照してください。

Feedthrough — 入力から出力への直達

0 (既定値) | 1 | logical ベクトル

入力から出力への直達。'Feedthrough' と長さ N_u の logical ベクトルで構成されるコンマ区切りのペアとして指定します。N_u は入力の数です。'Feedthrough' を logical スカラーとして指定すると、その値がすべての入力に適用されます。静的システムの場合、'Feedthrough' は常に 1 であると仮定されます。

例については、形式、直達、外乱モデルの行列の変更を参照してください。

DisturbanceModel — 時間領域のノイズ成分のパラメーターを推定するオプション

'estimate' | 'none'

K 行列で時間領域のノイズ成分のパラメーターを推定するオプション。'DisturbanceModel' と次の値のいずれかで構成されるコンマ区切りのペアとして指定します。

• 'estimate' — ノイズ成分を推定します。K 行列は自由パラメーターとして扱われます。時間領域データの場合、'estimate' が既定です。

• 'none' — ノイズ成分を推定しません。K 行列の要素はゼロで固定されます。周波数領域データの場合、'none' が既定であり、受け入れられる唯一の値です。

例については、形式、直達、外乱モデルの行列の変更を参照してください。

出力引数

sys — 同定された状態空間モデル

idss モデル

同定された状態空間モデル。idss モデルとして返されます。このモデルは、指定したモデル次数、遅延、および推定オプションを使用して作成されます。

推定結果と使用されたオプションに関する情報は、モデルの Report プロパティに格納されます。Report には次のフィールドがあります。

Report のフィールド	説明
Status	モデルのステータスの概要。モデルが構築によって作成されたものか推定によって取得されたものかを示します。
Method	使用された推定コマンド。
InitialState	推定時の初期状態の処理方法。次の値のいずれかとして返されます。 'zero' — 初期状態をゼロに設定。 'estimate' — 初期状態を独立した推定パラメーターとして処理。 このフィールドは、推定オプション セットで 'InitialState' オプションが 'auto' に設定されている場合に特に便利です。
N4Weight	N4SID アルゴリズムで特異値分解に使用された重み付けスキーム。次の値のいずれかとして返されます。 'MOESP' — MOESP アルゴリズムを使用。 'CVA' — 正準変量アルゴリズムを使用。 'SSARX' — 部分空間同定法で ARX の推定に基づくアルゴリズムを使用して重み付けを計算。 このオプションは、推定オプション セットで N4Weight オプションが 'auto' に設定されている場合に特に便利です。
N4Horizon	N4SID アルゴリズムで使用された前方および後方の予測範囲。3 要素の行ベクトル [r sy su] として返されます。ここで、r は前方予測範囲、sy は予測に使用された過去の出力の数、su は予測に使用された過去の入力の数です。
Fit	推定の定量的評価。構造体として返されます。これらの品質メトリクスの詳細については、Loss Function and Model Quality Metricsを参照してください。構造体には、以下のフィールドがあります。 フィールド 説明 FitPercent 正規化平方根平均二乗誤差 (NRMSE)。モデルの応答が推定データにどの程度適合するかをパーセンテージで示す尺度で、fitpercent = 100(1-NRMSE) として表されます。 LossFcn 推定完了時の損失関数の値。 MSE 平均二乗誤差 (MSE)。モデルの応答が推定データにどの程度適合するかを示す尺度です。 FPE モデルの最終予測誤差。 AIC 生の赤池情報量基準 (AIC)。モデルの品質を示す尺度です。 AICc 小さいサンプルサイズの補正された AIC。 nAIC 正規化された AIC。 BIC ベイズ情報量基準 (BIC)。
Parameters	モデル パラメーターの推定値。
OptionsUsed	推定に使用されたオプション セット。OptionsUsed は、カスタム オプションを構成していない場合は既定のオプションのセットになります。詳細については、n4sidOptions を参照してください。
RandState	推定開始時の乱数ストリームの状態。推定時にランダム化が使用されなかった場合は空 [] になります。詳細については、rng を参照してください。
DataUsed	推定に使用されたデータの属性。次のフィールドをもつ構造体として返されます。 フィールド 説明 Name データ セットの名前。 Type データ型。 Length データ サンプルの数。 Ts サンプル時間。 InterSample 入力サンプル間動作。次の値のいずれかとして返されます。 'zoh' — ゼロ次ホールドにより、サンプル間で区分的に一定な入力信号を維持。 'foh' — 1 次ホールドにより、サンプル間で区分的に線形な入力信号を維持。 'bl' — 帯域幅を制限した動作により、ナイキスト周波数を超える連続時間入力信号のパワーがゼロになるように指定。 InputOffset 推定時に時間領域の入力データから削除されたオフセット。非線形モデルの場合は [] になります。 OutputOffset 推定時に時間領域の出力データから削除されたオフセット。非線形モデルの場合は [] になります。

Report の使用の詳細については、Estimation Reportを参照してください。

x0 — 推定時に計算された初期状態

列ベクトル | 行列

推定時に計算された初期状態。各実験に対応する列ベクトルを含む配列として返されます。

この配列は、モデルの Report プロパティの Parameters フィールドにも格納されます。

参照

[1] Ljung, L. System Identification: Theory for the User, Appendix 4A, Second Edition, pp. 132–134. Upper Saddle River, NJ: Prentice Hall PTR, 1999.

[2] van Overschee, P., and B. De Moor. Subspace Identification of Linear Systems: Theory, Implementation, Applications. Springer Publishing: 1996.

[3] Verhaegen, M. "Identification of the deterministic part of MIMO state space models." Automatica, 1994, Vol. 30, pp. 61–74.

[4] Larimore, W.E. "Canonical variate analysis in identification, filtering and adaptive control." Proceedings of the 29th IEEE Conference on Decision and Control, 1990, pp. 596–604.

[5] McKelvey, T., H. Akcay, and L. Ljung. "Subspace-based multivariable system identification from frequency response data." IEEE Transactions on Automatic Control, 1996, Vol. 41, pp. 960–979.

バージョン履歴

R2006a より前に導入

R2022b: 時間領域推定データが timetable 形式および行列形式で受け入れられる

ほとんどの推定関数、検証関数、解析関数、およびユーティリティ関数が、時間領域入出力データを、入力と出力両方のデータを含む単一の timetable の形式、または、入力データと出力データを別々に含む行列のペアの形式で受け入れるようになりました。これらの関数は、時間領域データと周波数領域データの両方について、iddata オブジェクトを引き続きデータ ソースとして受け入れます。

参考

n4sidOptions | idss | ssest | tfest | procest | polyest | iddata | idfrd | idgrey | canon | pem

トピック

• 状態空間モデルとは
• Estimate State-Space Models at the Command Line
• State-Space Model Estimation Methods
• Estimate State-Space Models with Canonical Parameterization

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい