genrfeatures
構文
説明
関数 genrfeatures では、特徴量エンジニアリング プロセスを機械学習ワークフローのコンテキストで自動化できます。表形式の学習データを回帰モデルに渡す前に、genrfeatures を使用してデータ内の予測子から新しい特徴量を作成できます。返されたデータを使用して回帰モデルに学習させます。
genrfeatures を使用すると、datetime、duration やさまざまな int 型など、ほとんどの回帰モデルの学習関数でサポートされないデータ型の変数から特徴量を生成できます。結果の特徴量には、これらの学習関数でサポートされるデータ型が含まれています。
生成された特徴量について詳しく確認するには、返された FeatureTransformer オブジェクトの関数 describe を使用します。学習セットと同じ特徴変換をテスト セットに適用するには、FeatureTransformer オブジェクトの関数 transform を使用します。
[ は、自動特徴量エンジニアリングを使用して Transformer,NewTbl] = genrfeatures(Tbl,ResponseVarName,q)Tbl 内の予測子から q 個の特徴量を作成します。Tbl 内の変数 ResponseVarName は応答と見なされ、この変数からは新しい特徴量を作成しないものと仮定されます。genrfeatures は、FeatureTransformer オブジェクト (Transformer) と変換された特徴量が格納された新しい table (NewTbl) を返します。
既定では、genrfeatures は、生成された特徴量を解釈可能な線形回帰モデルの学習に使用するものと仮定します。バギング アンサンブルの精度を向上させるために特徴量を生成する場合は、TargetLearner="bag" を指定します。
[ は、ベクトル Transformer,NewTbl] = genrfeatures(Tbl,Y,q)Y が応答変数であると仮定し、Tbl 内の変数から新しい特徴量を作成します。
[ は、説明モデル Transformer,NewTbl] = genrfeatures(Tbl,formula,q)formula を使用して、Tbl 内の応答変数と Tbl 内の新しい特徴量の作成に使用する予測子のサブセットを判別します。
[ では、前の構文におけるいずれかの入力引数の組み合わせに加えて、1 つ以上の名前と値の引数を使用してオプションを指定します。たとえば、想定される学習器のタイプ、新しい特徴量の選択方法、変換されたデータの標準化方法を変更できます。Transformer,NewTbl] = genrfeatures(___,Name=Value)
例
自動特徴量エンジニアリングを使用して新しい特徴量を生成します。生成された特徴量を使用して線形回帰モデルに学習をさせます。生成された特徴量と学習させたモデルの関係を解釈します。
patients データ セットを読み込みます。変数のサブセットから table を作成します。テーブルの最初の数行を表示します。
load patients Tbl = table(Age,Diastolic,Gender,Height,SelfAssessedHealthStatus, ... Smoker,Weight,Systolic); head(Tbl)
Age Diastolic Gender Height SelfAssessedHealthStatus Smoker Weight Systolic
___ _________ __________ ______ ________________________ ______ ______ ________
38 93 {'Male' } 71 {'Excellent'} true 176 124
43 77 {'Male' } 69 {'Fair' } false 163 109
38 83 {'Female'} 64 {'Good' } false 131 125
40 75 {'Female'} 67 {'Fair' } false 133 117
49 80 {'Female'} 64 {'Good' } false 119 122
46 70 {'Female'} 68 {'Good' } false 142 121
33 88 {'Female'} 64 {'Good' } true 142 130
40 82 {'Male' } 68 {'Good' } false 180 115
Tbl の変数から新しい特徴量を 10 個生成します。応答として変数 Systolic を指定します。genrfeatures では、既定では新しい特徴量を線形回帰モデルの学習に使用すると見なします。
rng("default") % For reproducibility [T,NewTbl] = genrfeatures(Tbl,"Systolic",10)
T =
FeatureTransformer with properties:
Type: 'regression'
TargetLearner: 'linear'
NumEngineeredFeatures: 10
NumOriginalFeatures: 0
TotalNumFeatures: 10
NewTbl=100×11 table
zsc(d(Smoker)) q8(Age) eb8(Age) zsc(sin(Height)) zsc(kmd8) q6(Height) eb8(Diastolic) q8(Diastolic) zsc(fenc(c(SelfAssessedHealthStatus))) q10(Weight) Systolic
______________ _______ ________ ________________ _________ __________ ______________ _____________ ______________________________________ ___________ ________
1.3863 4 5 1.1483 -0.56842 6 8 8 0.27312 7 124
-0.71414 6 6 -0.3877 -2.0772 5 2 2 -1.4682 6 109
-0.71414 4 5 1.1036 -0.21519 2 4 5 0.82302 3 125
-0.71414 5 6 -1.4552 -0.32389 4 2 2 -1.4682 4 117
-0.71414 8 8 1.1036 1.2302 2 3 4 0.82302 1 122
-0.71414 7 7 -1.5163 -0.88497 4 1 1 0.82302 5 121
1.3863 3 3 1.1036 -1.1434 2 6 6 0.82302 5 130
-0.71414 5 6 -1.5163 -0.3907 4 4 5 0.82302 8 115
-0.71414 1 2 -1.5163 0.4278 4 3 3 0.27312 9 115
-0.71414 2 3 -0.26055 -0.092621 3 5 6 0.27312 3 118
-0.71414 7 7 -1.5163 0.16737 4 2 2 0.27312 2 114
-0.71414 6 6 -0.26055 -0.32104 3 1 1 -1.8348 5 115
-0.71414 1 1 1.1483 -0.051074 6 1 1 -1.8348 7 127
1.3863 5 5 0.14351 2.3695 6 8 8 0.27312 10 130
-0.71414 3 4 0.96929 0.092962 2 3 4 0.82302 3 114
1.3863 8 8 1.1483 -0.049336 6 7 8 0.82302 8 130
⋮
T は新しいデータの変換に使用できる FeatureTransformer オブジェクトで、newTbl には Tbl のデータから生成された新しい特徴量が格納されます。
生成された特徴量について詳しく確認するには、FeatureTransformer オブジェクトのオブジェクト関数 describe を使用します。たとえば、生成された最初の 2 つの特徴量を調べます。
describe(T,1:2)
Type IsOriginal InputVariables Transformations
___________ __________ ______________ ___________________________________________________________
zsc(d(Smoker)) Numeric false Smoker Variable of type double converted from an integer data type
Standardization with z-score (mean = 0.34, std = 0.4761)
q8(Age) Categorical false Age Equiprobable binning (number of bins = 8)
newTbl の 1 つ目の特徴量は数値変数で、最初に変数 Smoker の値を double 型の数値変数に変換してから、その結果を z スコアに変換して作成されています。newTbl の 2 つ目の特徴量はカテゴリカル変数で、変数 Age の値を 8 個の同確率のビンにビン化して作成されています。
生成された特徴量を使用して、正則化なしで線形回帰モデルを当てはめます。
Mdl = fitrlinear(NewTbl,"Systolic",Lambda=0);Mdl の学習に使用された予測子の係数をプロットします。fitrlinear では、モデルを当てはめる前にカテゴリカル予測子が展開されることに注意してください。
p = length(Mdl.Beta); [sortedCoefs,expandedIndex] = sort(Mdl.Beta,ComparisonMethod="abs"); sortedExpandedPreds = Mdl.ExpandedPredictorNames(expandedIndex); bar(sortedCoefs,Horizontal="on") yticks(1:2:p) yticklabels(sortedExpandedPreds(1:2:end)) xlabel("Coefficient") ylabel("Expanded Predictors") title("Coefficients for Expanded Predictors")
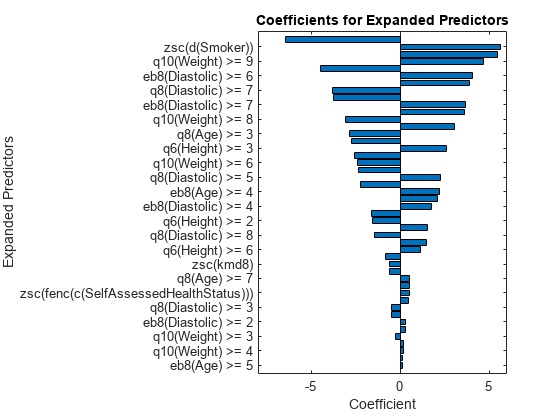
係数の絶対値が大きい予測子を特定します。
bigCoefs = abs(sortedCoefs) >= 4; flip(sortedExpandedPreds(bigCoefs))
ans = 1×6 cell
{'eb8(Diastolic) >= 5'} {'zsc(d(Smoker))'} {'q8(Age) >= 2'} {'q10(Weight) >= 9'} {'q6(Height) >= 5'} {'eb8(Diastolic) >= 6'}
部分依存プロットを使用して、絶対値に関して大きな係数をもつレベルのカテゴリカル特徴量を解析できます。たとえば、eb8(Diastolic) >= 5 と eb8(Diastolic) >= 6 のレベルで係数の絶対値が大きくなっている変数 eb8(Diastolic) の部分依存プロットを調べます。これらの 2 つのレベルは、予測した Systolic の値の目立った変化に対応します。
plotPartialDependence(Mdl,"eb8(Diastolic)",NewTbl);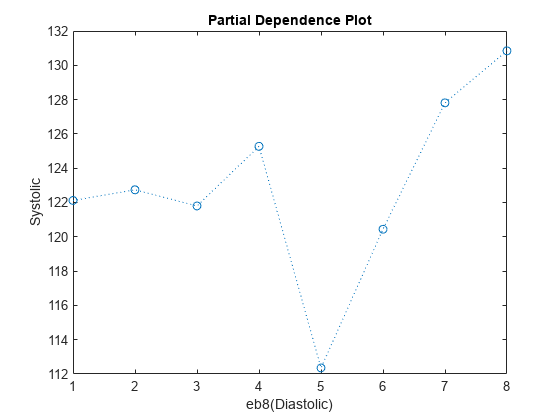
解釈可能な線形回帰モデルの予測性能を向上させるために新しい特徴量を生成します。元のデータで学習させた線形モデルのテスト セットの性能と変換された特徴量で学習させた線形モデルのテスト セットの性能を比較します。
carbig データ セットを読み込みます。このデータ セットには、1970 年代と 1980 年代初期に製造された自動車の測定値が格納されています。
load carbig変数 Origin をカテゴリカル変数に変換します。その後、Acceleration、Displacement などの予測子変数と応答変数 MPG を格納する table を作成します。各行に 1 台の自動車の測定値を格納します。欠損値が含まれている行を削除します。
Origin = categorical(cellstr(Origin));
cars = table(Acceleration,Displacement,Horsepower, ...
Model_Year,Origin,Weight,MPG);
Tbl = rmmissing(cars);データを学習セットとテスト セットに分割します。観測値の約 70% を学習データとして使用し、観測値の約 30% をテスト データとして使用します。データの分割には cvpartition を使用します。
rng("default") % For reproducibility of the partition c = cvpartition(size(Tbl,1),Holdout=0.3); trainIdx = training(c); trainTbl = Tbl(trainIdx,:); testIdx = test(c); testTbl = Tbl(testIdx,:);
学習データを使用して新しい特徴量を 45 個生成します。返された FeatureTransformer オブジェクトを調べます。
[T,newTrainTbl] = genrfeatures(trainTbl,"MPG",45);
TT =
FeatureTransformer with properties:
Type: 'regression'
TargetLearner: 'linear'
NumEngineeredFeatures: 43
NumOriginalFeatures: 2
TotalNumFeatures: 45
T.NumOriginalFeatures は 2 であり、元の予測子が 2 つ残っていることに注意してください。
オブジェクト T に格納された変換をテスト データに適用します。
newTestTbl = transform(T,testTbl);
元の特徴量で学習させた線形モデルと新しい特徴量で学習させた線形モデルのテスト セットの性能を比較します。
元の学習セット trainTbl を使用して線形回帰モデルに学習させ、元のテスト セット testTbl でモデルの平均二乗誤差 (MSE) を計算します。次に、変換後の学習セット newTrainTbl を使用して線形回帰モデルに学習させ、変換後のテスト セット newTestTbl でモデルの MSE を計算します。
originalMdl = fitrlinear(trainTbl,"MPG"); originalTestMSE = loss(originalMdl,testTbl,"MPG")
originalTestMSE = 65.9916
newMdl = fitrlinear(newTrainTbl,"MPG"); newTestMSE = loss(newMdl,newTestTbl,"MPG")
newTestMSE = 12.3010
newTestMSE が originalTestMSE より小さくなっており、変換後のデータで学習させた線形モデルの方が元のデータで学習させた線形モデルよりも性能が高くなっていることを示しています。
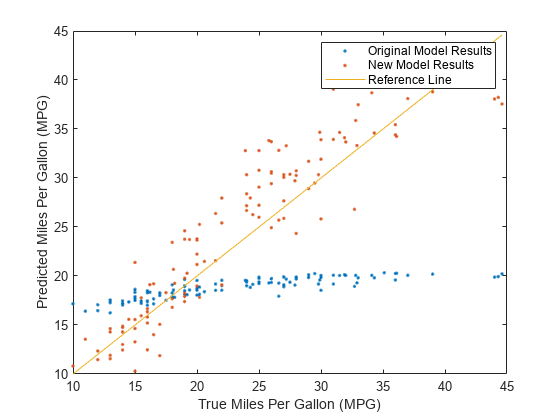
テスト セットの予測応答値と実際の応答値を両方のモデルで比較します。予測されるガロンあたりの走行マイル数 (MPG) を縦軸に、実際の MPG を横軸にしてプロットします。基準線上にある点は予測が正しいことを示します。優れたモデルでは、生成された予測が線の近くに分布します。
predictedTestY = predict(originalMdl,testTbl); newPredictedTestY = predict(newMdl,newTestTbl); plot(testTbl.MPG,predictedTestY,".") hold on plot(testTbl.MPG,newPredictedTestY,".") hold on plot(testTbl.MPG,testTbl.MPG) hold off xlabel("True Miles Per Gallon (MPG)") ylabel("Predicted Miles Per Gallon (MPG)") legend(["Original Model Results","New Model Results","Reference Line"])
バギング アンサンブル回帰モデルに学習させる前に、genrfeatures を使用して新しい特徴量を設計します。新しいデータの予測の前に同じ特徴変換を新しいデータ セットに適用します。設計した特徴量を使用するアンサンブルのテスト セット性能と元の特徴量を使用するアンサンブルのテスト セット性能を比較します。
停電のデータをワークスペースに table として読み込みます。欠損値がある観測値を削除し、table の最初の数行を表示します。
outages = readtable("outages.csv");
Tbl = rmmissing(outages);
head(Tbl) Region OutageTime Loss Customers RestorationTime Cause
_____________ ________________ ______ __________ ________________ ___________________
{'SouthWest'} 2002-02-01 12:18 458.98 1.8202e+06 2002-02-07 16:50 {'winter storm' }
{'SouthEast'} 2003-02-07 21:15 289.4 1.4294e+05 2003-02-17 08:14 {'winter storm' }
{'West' } 2004-04-06 05:44 434.81 3.4037e+05 2004-04-06 06:10 {'equipment fault'}
{'MidWest' } 2002-03-16 06:18 186.44 2.1275e+05 2002-03-18 23:23 {'severe storm' }
{'West' } 2003-06-18 02:49 0 0 2003-06-18 10:54 {'attack' }
{'NorthEast'} 2003-07-16 16:23 239.93 49434 2003-07-17 01:12 {'fire' }
{'MidWest' } 2004-09-27 11:09 286.72 66104 2004-09-27 16:37 {'equipment fault'}
{'SouthEast'} 2004-09-05 17:48 73.387 36073 2004-09-05 20:46 {'equipment fault'}
変数の中には、OutageTime や RestorationTime など、fitrensemble のような回帰モデル学習関数でサポートされないデータ型の変数も含まれています。
データを学習セットとテスト セットに分割します。観測値の約 70% を学習データとして使用し、観測値の約 30% をテスト データとして使用します。データの分割には cvpartition を使用します。
rng("default") % For reproducibility of the partition c = cvpartition(size(Tbl,1),Holdout=0.30); TrainTbl = Tbl(training(c),:); TestTbl = Tbl(test(c),:);
学習データを使用して、バギング アンサンブルの当てはめに使用する新しい特徴量を 30 個生成します。既定では、30 個の特徴量の中にバギング アンサンブルで予測子として使用できる元の特徴量が含まれます。
[Transformer,NewTrainTbl] = genrfeatures(TrainTbl,"Loss",30, ... TargetLearner="bag"); Transformer
Transformer =
FeatureTransformer with properties:
Type: 'regression'
TargetLearner: 'bag'
NumEngineeredFeatures: 27
NumOriginalFeatures: 3
TotalNumFeatures: 30
オブジェクト Transformer に格納された変換をテスト データに適用して NewTestTbl を作成します。
NewTestTbl = transform(Transformer,TestTbl);
元の学習セット TrainTbl を使用してバギング アンサンブルに学習させ、元のテスト セット TestTbl でモデルの平均二乗誤差 (MSE) を計算します。fitrensemble が使用できる 3 つの予測子変数 (Region、Customers、および Cause) のみ指定し、2 つの datetime 予測子変数 (OutageTime および RestorationTime) を省略します。次に、変換後の学習セット NewTrainTbl を使用してバギング アンサンブルに学習させ、変換後のテスト セット NewTestTbl でモデルの MSE を計算します。
originalMdl = fitrensemble(TrainTbl,"Loss ~ Region + Customers + Cause", ... Method="bag"); originalTestMSE = loss(originalMdl,TestTbl)
originalTestMSE = 1.8999e+06
newMdl = fitrensemble(NewTrainTbl,"Loss",Method="bag"); newTestMSE = loss(newMdl,NewTestTbl)
newTestMSE = 1.8617e+06
newTestMSE が originalTestMSE より小さくなっており、変換後のデータで学習させたバギング アンサンブルの方が元のデータで学習させたバギング アンサンブルよりも性能がわずかに高くなっていることを示しています。
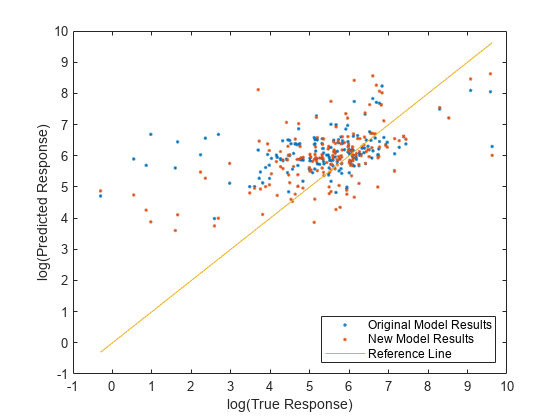
テスト セットの予測応答値と実際の応答値を両方のモデルで比較します。予測応答の対数を縦軸に、実際の応答 (Loss) の対数を横軸に沿ってプロットします。基準線上にある点は予測が正しいことを示します。優れたモデルでは、生成された予測が線の近くに分布します。
predictedTestY = predict(originalMdl,TestTbl); newPredictedTestY = predict(newMdl,NewTestTbl); plot(log(TestTbl.Loss),log(predictedTestY),".") hold on plot(log(TestTbl.Loss),log(newPredictedTestY),".") hold on plot(log(TestTbl.Loss),log(TestTbl.Loss)) hold off xlabel("log(True Response)") ylabel("log(Predicted Response)") legend(["Original Model Results","New Model Results","Reference Line"], ... Location="southeast") xlim([-1 10]) ylim([-1 10])
ガウス カーネルを使用したサポート ベクター マシン (SVM) 回帰モデルに学習させる前に、新しい特徴量を設計して検査します。その後、モデルのテスト セット性能を評価します。
carbig データ セットを読み込みます。このデータ セットには、1970 年代と 1980 年代初期に製造された自動車の測定値が格納されています。
load carbigAcceleration、Displacement などの数値予測子変数と応答変数 MPG が格納された table を作成します。各行に 1 台の自動車の測定値を格納します。欠損値が含まれている行を削除します。
cars = table(Acceleration,Displacement,Horsepower, ...
Model_Year,Weight,MPG);
Tbl = rmmissing(cars);
head(Tbl) Acceleration Displacement Horsepower Model_Year Weight MPG
____________ ____________ __________ __________ ______ ___
12 307 130 70 3504 18
11.5 350 165 70 3693 15
11 318 150 70 3436 18
12 304 150 70 3433 16
10.5 302 140 70 3449 17
10 429 198 70 4341 15
9 454 220 70 4354 14
8.5 440 215 70 4312 14
データを学習セットとテスト セットに分割します。観測値の約 75% を学習データとして使用し、観測値の約 25% をテスト データとして使用します。データの分割には cvpartition を使用します。
rng("default") % For reproducibility of the partition n = length(Tbl.MPG); c = cvpartition(n,Holdout=0.25); trainTbl = Tbl(training(c),:); testTbl = Tbl(test(c),:);
学習データを使用して、ガウス カーネルを使用した SVM 回帰モデルの当てはめに使用する特徴量を 25 個生成します。既定では、25 個の特徴量の中に SVM 回帰モデルで予測子として使用できる元の特徴量が含まれます。さらに、genrfeatures は、近傍成分分析 (NCA) を使用して、設計された特徴量のセットを最も重要な予測子に絞り込みます。NCA 特徴選択手法は、ターゲットの学習器が "gaussian-svm" の場合にのみ使用できます。
[Transformer,newTrainTbl] = genrfeatures(trainTbl,"MPG",25, ... TargetLearner="gaussian-svm")
Transformer =
FeatureTransformer with properties:
Type: 'regression'
TargetLearner: 'gaussian-svm'
NumEngineeredFeatures: 20
NumOriginalFeatures: 5
TotalNumFeatures: 25
newTrainTbl=294×26 table
zsc(Acceleration) zsc(Displacement) zsc(Horsepower) zsc(Model_Year) zsc(Weight) zsc(Acceleration.*Horsepower) zsc(Acceleration-Model_Year) zsc(sin(Displacement)) zsc(sin(Horsepower)) zsc(sin(Model_Year)) zsc(sin(Weight)) zsc(cos(Acceleration)) zsc(cos(Displacement)) zsc(cos(Model_Year)) zsc(cos(Weight)) q12(Acceleration) q12(Displacement) q12(Horsepower) q6(Model_Year) q19(Weight) eb12(Acceleration) eb7(Displacement) eb9(Horsepower) eb6(Model_Year) eb7(Weight) MPG
_________________ _________________ _______________ _______________ ___________ _____________________________ ____________________________ ______________________ ____________________ ____________________ ________________ ______________________ ______________________ ____________________ ________________ _________________ _________________ _______________ ______________ ___________ __________________ _________________ _______________ _______________ ___________ ___
-1.2878 1.0999 0.67715 -1.6278 0.6473 0.046384 0.58974 -0.95649 -1.3699 1.1059 -1.2446 1.2301 1.0834 0.88679 -0.63765 2 10 10 1 14 3 6 5 1 5 18
-1.4652 1.5106 1.5694 -1.6278 0.87016 0.88366 0.46488 -1.2198 1.3794 1.1059 -1.379 0.72852 -0.27316 0.88679 0.063193 1 11 11 1 15 2 7 7 1 5 15
-1.6425 1.2049 1.187 -1.6278 0.56711 0.26966 0.34001 -0.78431 -1.063 1.1059 -1.0814 0.062328 -0.98059 0.88679 0.86743 1 11 11 1 14 2 6 6 1 4 18
-1.8198 1.0521 0.93209 -1.6278 0.58244 -0.17689 0.21515 0.65123 1.3543 1.1059 -0.61728 -0.60537 1.4918 0.88679 1.2572 1 10 10 1 14 1 6 6 1 4 17
-1.9971 2.2653 2.4107 -1.6278 1.6343 1.0883 0.090291 1.4649 -0.157 1.1059 -0.86513 -1.1111 -0.10886 0.88679 1.0923 1 12 12 1 18 1 7 8 1 6 15
-2.3517 2.5041 2.9716 -1.6278 1.6496 1.0883 -0.15943 1.4843 0.08254 1.1059 -0.329 -1.2114 0.084822 0.88679 1.368 1 12 12 1 18 1 7 9 1 6 14
-2.529 2.3704 2.8441 -1.6278 1.6001 0.71 -0.28429 0.34762 1.3544 1.1059 1.3872 -0.78132 1.5888 0.88679 -0.2533 1 12 12 1 18 1 7 9 1 6 14
-2.529 1.8927 2.2068 -1.6278 1.0553 0.18283 -0.28429 0.69577 1.3794 1.1059 -1.381 -0.78132 1.4703 0.88679 -0.050724 1 12 12 1 16 1 7 8 1 5 15
-1.9971 1.8259 1.6969 -1.6278 0.71687 0.3937 0.090291 -0.26965 0.45082 1.1059 0.59822 -1.1111 1.5569 0.88679 1.279 1 12 12 1 15 1 7 7 1 5 15
-2.7063 1.4151 1.442 -1.6278 0.77111 -0.64825 -0.40916 1.0025 0.26939 1.1059 0.89932 -0.14624 1.2589 0.88679 -1.1233 1 11 11 1 15 1 6 7 1 5 14
-1.9971 2.5137 3.0991 -1.6278 0.1544 1.7582 0.090291 0.80367 -1.3699 1.1059 1.1507 -1.1111 -1.1229 0.88679 0.80592 1 12 12 1 12 1 7 9 1 4 14
-0.22399 -0.75341 -0.21514 -1.6278 -0.68753 -0.28853 1.3389 -0.029778 0.93084 1.1059 -0.12343 -1.0007 1.6048 0.88679 -1.4439 6 4 7 1 7 6 2 3 1 2 24
-0.046679 0.058585 -0.21514 -1.6278 -0.14393 -0.17069 1.4638 -0.0054687 0.93084 1.1059 -0.90303 -1.305 -1.3204 0.88679 1.0596 7 8 7 1 10 6 3 3 1 3 22
0.13063 0.077691 -0.47008 -1.6278 -0.43401 -0.44978 1.5886 -1.1016 -0.29461 1.1059 -1.3741 -1.2761 0.85875 0.88679 -0.16461 8 8 5 1 8 7 4 3 1 3 21
1.7264 -0.90626 -1.4643 -1.6278 -1.3207 -1.4843 2.7124 0.62866 1.2425 1.1059 0.43728 -0.054514 -1.2152 0.88679 1.3434 12 3 1 1 1 11 1 1 1 1 26
0.66256 -0.83939 -0.21514 -1.6278 -0.68399 0.30067 1.9632 -0.33972 0.93084 1.1059 -0.049071 0.36145 -1.2471 0.88679 1.4102 10 4 7 1 7 8 2 3 1 2 25
⋮
既定では、genrfeatures は、元の特徴量を newTrainTbl に含める前に標準化します。
設計された最初の 3 つの特徴量を検査します。設計された特徴量は、Transformer オブジェクトにおいて、元の 5 個の特徴量の後に格納されることに注意してください。散布図とヒストグラムの行列を使用して、設計された特徴量を可視化します。
featIndex = 6:8; describe(Transformer,featIndex)
Type IsOriginal InputVariables Transformations
_______ __________ ________________________ _______________________________________________________________
zsc(Acceleration.*Horsepower) Numeric false Acceleration, Horsepower Acceleration .* Horsepower
Standardization with z-score (mean = 1541.3031, std = 403.0917)
zsc(Acceleration-Model_Year) Numeric false Acceleration, Model_Year Acceleration - Model_Year
Standardization with z-score (mean = -60.3616, std = 4.0044)
zsc(sin(Displacement)) Numeric false Displacement sin( )
Standardization with z-score (mean = -0.075619, std = 0.72413)
plotmatrix(newTrainTbl{:,featIndex})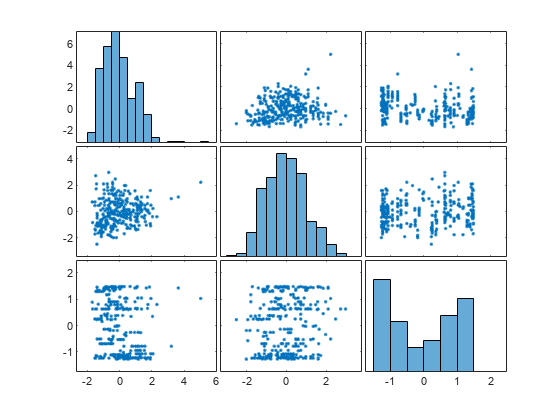
プロットは設計された特徴量について詳しく確認するのに役立ちます。以下に例を示します。
左上のプロットは、特徴量
zsc(Acceleration.*Horsepower)のヒストグラムです。この特徴量は、元の特徴量AccelerationとHorsepowerの標準化された要素単位の積で構成されます。このヒストグラムから、zsc(Acceleration.*Horsepower)に 3 よりも大きい外れ値はほとんどないことがわかります。左下のプロットは、
zsc(Acceleration.*Horsepower)の値 (x 軸方向) をzsc(Horsepower.*Weight)の値 (y 軸方向) と比較する散布図です。この散布図から、zsc(Acceleration.*Horsepower)の値が大きくなるとzsc(Horsepower.*Weight)の値も大きくなる傾向にあることがわかります。このプロットに含まれる情報は右上のプロットと同じですが、座標軸が入れ替わっていることに注意してください。
オブジェクト Transformer に格納された変換をテスト データに適用して newTestTbl を作成します。
newTestTbl = transform(Transformer,testTbl);
変換後の学習セット newTrainTbl を使用して、ガウス カーネルを使用した SVM 回帰モデルに学習させます。関数 fitrsvm でカーネル関数に対応する適切なスケール値を特定します。変換後のテスト セット newTestTbl でモデルの平均二乗誤差 (MSE) を計算します。
Mdl = fitrsvm(newTrainTbl,"MPG",KernelFunction="gaussian", ... KernelScale="auto"); testMSE = loss(Mdl,newTestTbl,"MPG")
testMSE = 8.3955
テスト セットの予測応答値と実際の応答値を比較します。予測されるガロンあたりの走行マイル数 (MPG) を縦軸に、実際の MPG を横軸にしてプロットします。基準線上にある点は予測が正しいことを示します。優れたモデルでは、生成された予測が線の近くに分布します。
predictedTestY = predict(Mdl,newTestTbl); plot(newTestTbl.MPG,predictedTestY,".") hold on plot(newTestTbl.MPG,newTestTbl.MPG) hold off xlabel("True Miles Per Gallon (MPG)") ylabel("Predicted Miles Per Gallon (MPG)")
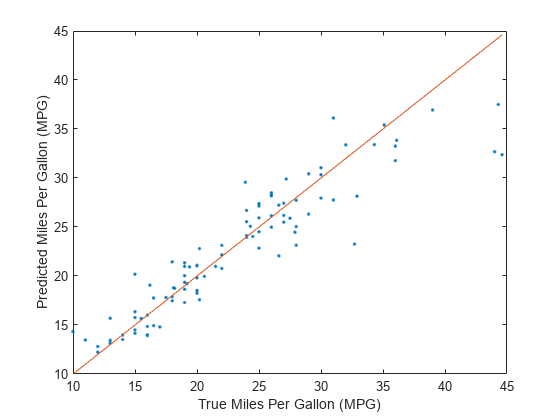
SVM モデルは、MPG の値を正しく予測していると考えられます。
特徴量を生成して線形回帰モデルに学習させます。関数 crossval を使用して、モデルの交差検証平均二乗誤差 (MSE) を計算します。
patients データ セットを読み込み、予測子データが含まれている table を作成します。
load patients Tbl = table(Age,Diastolic,Gender,Height,SelfAssessedHealthStatus, ... Smoker,Weight);
5 分割交差検証用に無作為分割を作成します。
rng("default") % For reproducibility of the partition cvp = cvpartition(size(Tbl,1),KFold=5);
Tbl 内の元の特徴量および Systolic 応答変数で学習させた線形回帰モデルについて、交差検証 MSE を計算します。
CVMdl = fitrlinear(Tbl,Systolic,CVPartition=cvp); cvloss = kfoldLoss(CVMdl)
cvloss = 45.2990
カスタム関数 myloss (この例の終わりに掲載) を作成します。この関数は、学習データから 20 個の特徴量を生成し、学習セットと同じ変換をテスト データに適用します。その後、線形回帰モデルを学習データに当てはめ、テスト セット MSE を計算します。
メモ: この例のライブ スクリプト ファイルを使用している場合、関数 myloss は既にファイルの終わりに含まれています。それ以外の場合は、この関数を .m ファイルの終わりに作成するか、MATLAB® パス上のファイルとして追加する必要があります。
Tbl 内の予測子から生成された特徴量で学習させた線形モデルについて、交差検証 MSE を計算します。
newcvloss = mean(crossval(@myloss,Tbl,Systolic,Partition=cvp))
newcvloss = 26.9963
function testloss = myloss(TrainTbl,trainY,TestTbl,testY) [Transformer,NewTrainTbl] = genrfeatures(TrainTbl,trainY,20); NewTestTbl = transform(Transformer,TestTbl); Mdl = fitrlinear(NewTrainTbl,trainY); testloss = loss(Mdl,NewTestTbl,testY); end
入力引数
元の特徴量。table として指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。オプションとして、Tbl に応答変数用の列を 1 つ追加できます。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できませんが、datetime、duration およびさまざまな int 予測子変数は使用できます。
Tblに応答変数が含まれている場合にTbl内の他のすべての変数から新しい特徴量を作成するには、ResponseVarNameを使用して応答変数を指定します。Tblに応答変数が含まれている場合にTbl内の他の変数の一部のみから新しい特徴量を作成するには、formulaを使用して式を指定します。Tblに応答変数が含まれていない場合は、Yを使用して応答変数を指定します。応答変数の長さとTblの行数は等しくなければなりません。
データ型: table
応答変数の名前。Tbl 内の変数の名前で指定します。
ResponseVarName には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、応答変数 Y が Tbl.Y として格納されている場合、'Y' として指定します。それ以外の場合、Tbl の列はすべて予測子として扱われ、Y から新しい特徴量が作成されることがあります。
データ型: char | string
特徴量の個数。正の整数スカラーとして指定します。たとえば、q を 1.5*size(Tbl,2) のように設定すると、元の特徴量の個数の約 1.5 倍に設定できます。
データ型: single | double
応答変数。数値列ベクトルとして指定します。Y と Tbl の行数は同じでなければなりません。
データ型: single | double
応答変数および予測子変数サブセットの説明モデル。"Y~X1+X2+X3" という形式の文字ベクトルまたは string スカラーを指定します。この式では、Y は応答変数を、X1、X2 および X3 は予測子変数を表します。
Tbl 内の予測子変数のサブセットのみから新しい特徴量を作成するには、式を使用します。式を指定した場合、formula に現れない Tbl 内の変数からは特徴量は作成されません。
式の変数名は Tbl の変数名 (Tbl.Properties.VariableNames) であり、有効な MATLAB® 識別子でなければなりません。関数 isvarname を使用して Tbl の変数名を検証できます。変数名が有効でない場合、関数 matlab.lang.makeValidName を使用してそれらを変換できます。
データ型: char | string
名前と値の引数
オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。
例: genrfeatures(Tbl,"Response",10,TargetLearner="bag",FeatureSelection="oob") は、想定される学習器のタイプをバギング アンサンブル回帰モデル、特徴量の選択方法を out-of-bag 予測子の重要度の手法と指定します。
想定される学習器のタイプ。"linear"、"bag"、または "gaussian-svm" として指定します。このタイプのモデルの学習に使用されることを想定し、それに応じて新しい特徴量が作成および選択されます。
| 値 | 想定されるモデル |
|---|---|
"linear" | RegressionLinear — このモデルは、関数 fitrlinear を使用して作成できます。 |
"bag" | RegressionBaggedEnsemble — このモデルは、関数 fitrensemble を使用して Method="Bag" を指定することで作成できます。 |
"gaussian-svm" | RegressionSVM (ガウス カーネルを使用) — このモデルは、関数 fitrsvm を使用して KernelFunction="gaussian" を指定することで作成できます。予測性能が高いモデルを作成するには、KernelScale="auto" を指定します。 |
例: TargetLearner="bag"
Tbl 内の元の特徴量を新しい table NewTbl に含める方法。次の表のいずれかの値として指定します。
| 値 | 説明 |
|---|---|
"auto" | この値は以下と等価です。
|
"include" | 元の特徴量のうち、ターゲットの学習器で予測子として使用できる特徴量が含められます。次の特徴量は除外されます。
|
"select" | 元の特徴量のうち、ターゲットの学習器でサポートされ、指定された特徴選択方法 (FeatureSelectionMethod) で重要と見なされる特徴量が含められます。 |
"omit" | 元の特徴量は省略されます。 |
名前と値の引数 TransformedDataStandardization で指定される標準化方法が NewTbl に含まれる元の特徴量に適用されることに注意してください。
例: IncludeInputVariables="include"
新しい特徴量の選択方法。次の表のいずれかの値として指定します。各種の変換を使用して生成される多くの特徴量の中から、この方法を使用して NewTbl に含める重要な特徴量が選択されます。
| 値 | 説明 |
|---|---|
"auto" | この値は以下と等価です。
|
"lasso" | LASSO 正則化 — 特徴選択を実行するために、 |
"oob" | 並べ替えによる out-of-bag 予測子の重要度の推定 — 特徴選択を実行するために、木のバギング アンサンブルを当てはめ、関数 |
"nca" | 近傍成分分析 (NCA) — 特徴選択を実行するために、
|
"mrmr" | Minimum Redundancy Maximum Relevance (MRMR) — 特徴選択を実行するために、 |
各種の特徴選択手法の詳細については、特徴選択の紹介を参照してください。
例: FeatureSelection="mrmr"
変換されたデータの標準化方法。次の表のいずれかの値として指定します。この標準化方法は、設計済みの特徴量および元の特徴量の両方に適用されます。
| 値 | 説明 |
|---|---|
"auto" | この値は以下と等価です。
|
"zscore" | 平均が 0、標準偏差が 1 になるようにセンタリングしてスケーリング |
"none" | 生データを使用 |
"mad" | 中央値が 0、中央絶対偏差が 1 になるようにセンタリングしてスケーリング |
"range" | データの範囲を [0,1] にスケーリング |
例: TransformedDataStandardization="range"
カテゴリカル予測子で許容される最大カテゴリ数。非負の整数スカラーとして指定します。指定した数を超えるカテゴリがカテゴリカル予測子に含まれている場合、genrfeatures はその予測子からは新しい特徴量を作成せず、新しい table NewTbl から予測子を除外します。既定値は、TargetLearner が "linear" または "gaussian-svm" の場合は 50、TargetLearner が "bag" の場合は Inf です。
例: CategoricalEncodingLimit=20
データ型: single | double
出力引数
設計された特徴量の変換器。FeatureTransformer オブジェクトとして返されます。設計された特徴量について詳しく確認するには、Transformer のオブジェクト関数 describe を使用します。同じ特徴変換を新しいデータ セットに適用するには、Transformer のオブジェクト関数 transform を使用します。
生成された特徴量。table として返されます。各行が観測値に対応し、各列が生成された特徴量に対応します。Tbl に応答変数が含まれている場合、NewTbl にも応答変数が含まれます。この table を使用して、TargetLearner のタイプの回帰モデルに学習させます。
NewTbl には、元の特徴量、設計された特徴量 (特徴選択方法によるランク付けに応じて)、応答変数の順に、生成された特徴量が格納されます。
ヒント
既定では、
TargetLearnerが"linear"または"gaussian-svm"の場合、数値予測子からの新しい特徴量の生成に z スコアが使用されます (TransformedDataStandardizationを参照)。変換された特徴量の標準化のタイプは変更できます。ただし、"none"は指定せず、いずれかの標準化の方法を使用することを強くお勧めします。線形モデルおよび SVM モデルの当てはめは、標準化されたデータで最も適切に機能します。予測性能が高い SVM モデルを作成するには、特徴量を生成する際に、
fitrsvmの呼び出しでKernelScaleを"auto"として指定します。このように指定すると、SVM カーネル関数に対応する適切なスケール値が特定されます。
バージョン履歴
R2021b で導入TargetLearner が "linear" または "gaussian-svm" の場合、関数 genrfeatures は、IncludeInputVariables が "include" と指定されていても、欠損値を含むカテゴリカルの元の特徴量を常に除外します。つまり、これらの特徴量は生成された特徴量の table NewTbl に含まれません。また、genrfeatures は、それらの欠損値を含むカテゴリカル特徴量からは特徴量を生成しません。
欠損値を含む元のカテゴリカル特徴量を NewTbl に含めるには、事前に関数 rmmissing を使用して、欠損値がある観測値を Tbl から削除しておきます。
ガウス カーネルを使用した SVM モデルに学習させる前に、数値予測子とカテゴリカル予測子が混在するデータ セットから新しい特徴量を設計し、新しい特徴量を選択する手法として近傍成分分析 (NCA) を使用できます (FeatureSelectionMethod="nca")。genrfeatures の呼び出しで TargetLearner を "gaussian-svm" として指定します。
以前のリリースでは、数値予測子を含むデータ セットに対してのみ NCA 特徴選択手法を使用できました。
TargetLearner が "linear" または "gaussian-svm" の場合、関数 genrfeatures は、IncludeInputVariables が "include" と指定されていても、NaN または Inf の値を含む元の特徴量を常に除外します。つまり、これらの特徴量は生成された特徴量の table NewTbl に含まれません。また、genrfeatures は、NaN 値を含む元の特徴量からは特徴量を生成しません。
NaN 値を含む元の特徴量を NewTbl に含めるには、事前に関数 rmmissing を使用して、欠損値がある観測値を Tbl から削除しておきます。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)