fitrensemble
回帰のアンサンブル学習器の当てはめ
構文
説明
Mdl = fitrensemble(Tbl,ResponseVarName)Tbl 内の予測子および応答データを使用して 100 本の回帰木をブースティングした結果が格納されている学習済みのアンサンブル回帰モデル オブジェクト (Mdl) を返します。ResponseVarName は、Tbl 内の応答変数の名前です。
Mdl = fitrensemble(___,Name,Value)Name,Value ペア引数で指定される追加のオプションと、前の構文の入力引数のいずれかを使用します。たとえば、学習サイクル数、アンサンブル集約法、10 分割交差検証の実施を指定できます。
例
アンサンブル回帰に学習をさせる
与えられた気筒数、気筒ごとの排気量、馬力および重量に対して自動車の燃費を予測するアンサンブル回帰を作成します。次に、予測子の数を減らして、別のアンサンブルに学習をさせます。これらのアンサンブルの標本内予測精度を比較します。
carsmall データセットを読み込みます。学習に使用する変数をテーブルに格納します。
load carsmall
Tbl = table(Cylinders,Displacement,Horsepower,Weight,MPG);アンサンブル回帰に学習をさせます。
Mdl1 = fitrensemble(Tbl,'MPG');Mdl1 は RegressionEnsemble モデルです。Mdl1 には、次のような顕著な特徴があります。
アンサンブル集約アルゴリズムは
'LSBoost'です。アンサンブル集約アルゴリズムがブースティング アルゴリズムなので、最大 10 分割を許容する回帰木がアンサンブルを構成します。
100 本の木がアンサンブルを構成します。
MPG は MATLAB® ワークスペースの変数なので、次のように入力すると同じ結果を得ることができます。
Mdl1 = fitrensemble(Tbl,MPG);
学習させたアンサンブル回帰を使用して、排気量が 200 立方インチ、150 馬力、重量 3,000 lbs の 4 気筒搭載車の燃費を予測します。
pMPG = predict(Mdl1,[4 200 150 3000])
pMPG = 25.6467
Displacement を除く Tbl 内の予測子をすべて使用して、新しいアンサンブルに学習をさせます。
formula = 'MPG ~ Cylinders + Horsepower + Weight';
Mdl2 = fitrensemble(Tbl,formula);Mdl1 と Mdl2 の再代入 MSE を比較します。
mse1 = resubLoss(Mdl1)
mse1 = 0.3096
mse2 = resubLoss(Mdl2)
mse2 = 0.5861
すべての予測子に対して学習を行ったアンサンブルの方が、標本内 MSE が小さくなります。
数値予測子の値のビン化による学習の高速化
fitrensemble を使用して、ブースティング回帰木のアンサンブルに学習をさせます。名前と値のペアの引数 'NumBins' を指定して数値予測子をビン化することにより、学習時間を短縮します。学習後、学習済みモデルの BinEdges プロパティと関数discretizeを使用して、ビン化された予測子データを再現できます。
標本データセットを生成します。
rng('default') % For reproducibility N = 1e6; X1 = randi([-1,5],[N,1]); X2 = randi([5,10],[N,1]); X3 = randi([0,5],[N,1]); X4 = randi([1,10],[N,1]); X = [X1 X2 X3 X4]; y = X1 + X2 + X3 + X4 + normrnd(0,1,[N,1]);
最小二乗ブースティング (LSBoost、既定値) を使用して、ブースティング回帰木のアンサンブルに学習をさせます。比較のため、関数の実行時間を測定します。
tic Mdl1 = fitrensemble(X,y); toc
Elapsed time is 78.662954 seconds.
名前と値のペアの引数 'NumBins' を使用して、学習を高速化します。'NumBins' の値として正の整数スカラーを指定した場合、指定した個数の同確率のビンにすべての数値予測子がビン化され、元のデータではなくビンのインデックスに対して木が成長します。カテゴリカル予測子はビン化されません。
tic
Mdl2 = fitrensemble(X,y,'NumBins',50);
tocElapsed time is 43.353208 seconds.
元のデータではなくビン化されたデータを使用すると、処理が約 2 倍高速になります。経過時間はオペレーティング システムによって変化する可能性があることに注意してください。
再代入による回帰誤差を比較します。
rsLoss = resubLoss(Mdl1)
rsLoss = 1.0134
rsLoss2 = resubLoss(Mdl2)
rsLoss2 = 1.0133
この例では、予測子の値をビン化することにより、精度を大きく失わずに学習時間が短縮されました。一般に、この例のような大規模な学習データセットを使用する場合、ビン化オプションを使用すると学習を高速化できますが、精度が低下する可能性があります。さらに学習時間を短縮するには、指定するビンの個数を少なくします。
学習済みモデルの BinEdges プロパティと関数discretizeを使用して、ビン化された予測子データを再現します。
X = Mdl2.X; % Predictor data Xbinned = zeros(size(X)); edges = Mdl2.BinEdges; % Find indices of binned predictors. idxNumeric = find(~cellfun(@isempty,edges)); if iscolumn(idxNumeric) idxNumeric = idxNumeric'; end for j = idxNumeric x = X(:,j); % Convert x to array if x is a table. if istable(x) x = table2array(x); end % Group x into bins by using the discretize function. xbinned = discretize(x,[-inf; edges{j}; inf]); Xbinned(:,j) = xbinned; end
数値予測子の場合、1 からビンの個数までの範囲にあるビンのインデックスが Xbinned に格納されます。カテゴリカル予測子の場合、Xbinned の値は 0 になります。X に NaN が含まれている場合、対応する Xbinned の値は NaN になります。
ブースティング アンサンブルの汎化誤差の推定
ブースティング回帰木のアンサンブルの汎化誤差を推定します。
carsmall データセットを読み込みます。燃費の予測子として、気筒数、気筒ごとの排気量、馬力、重量を選択します。
load carsmall
X = [Cylinders Displacement Horsepower Weight];10 分割の交差検証を使用して、回帰木のアンサンブルを交差検証します。決定木テンプレートを使用して、各木を 1 回だけ分割するように指定します。
rng(1); % For reproducibility t = templateTree('MaxNumSplits',1); Mdl = fitrensemble(X,MPG,'Learners',t,'CrossVal','on');
Mdl は RegressionPartitionedEnsemble モデルです。
10 分割交差検証を行った累積平均二乗誤差 (MSE) をプロットします。アンサンブルの推定汎化誤差を表示します。
kflc = kfoldLoss(Mdl,'Mode','cumulative'); figure; plot(kflc); ylabel('10-fold cross-validated MSE'); xlabel('Learning cycle');
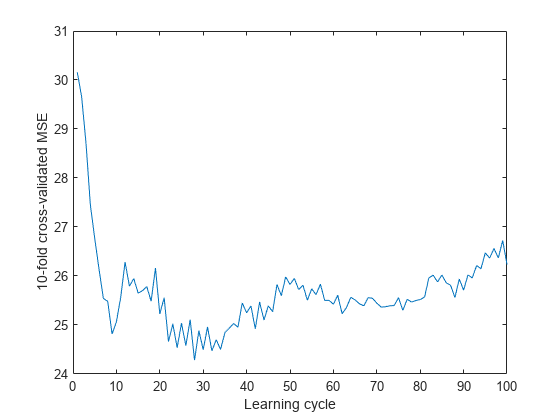
estGenError = kflc(end)
estGenError = 26.2356
既定の設定では、kfoldLoss は汎化誤差を返します。しかし、累積損失をプロットすると、アンサンブル内に弱学習器が蓄積するにつれて損失がどのように変化するかを観察できます。
このアンサンブルでは、約 30 個の弱学習器が蓄積した後の MSE が約 23.5 になっています。
アンサンブルの汎化誤差が満足できるものになった場合は、予測モデルを作成するため、交差検証以外の設定をすべて使用して、再度アンサンブルに学習をさせます。ただし、木あたりの決定分岐の最大数や学習サイクル数などのハイパーパラメーターを調整することをお勧めします。
アンサンブル回帰の最適化
この例では、fitrensemble を使用して自動的にハイパーパラメーターを最適化する方法を示します。この例では、carsmall データを使用します。
データを読み込みます。
load carsmall自動的なハイパーパラメーター最適化を使用して、5 分割交差検証損失を最小化するハイパーパラメーターを求めることができます。
Mdl = fitrensemble([Horsepower,Weight],MPG,'OptimizeHyperparameters','auto')
この例では、再現性を得るため、乱数シードを設定し、'expected-improvement-plus' の獲得関数を使用します。また、ランダム フォレスト アルゴリズムの再現性を得るため、木学習器について名前と値のペアの引数 'Reproducible' として true を指定します。
rng('default') t = templateTree('Reproducible',true); Mdl = fitrensemble([Horsepower,Weight],MPG,'OptimizeHyperparameters','auto','Learners',t, ... 'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName','expected-improvement-plus'))
|===================================================================================================================================| | Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Method | NumLearningC-| LearnRate | MinLeafSize | | | result | log(1+loss) | runtime | (observed) | (estim.) | | ycles | | | |===================================================================================================================================| | 1 | Best | 2.9726 | 14.487 | 2.9726 | 2.9726 | Bag | 413 | - | 1 | | 2 | Accept | 6.2619 | 1.2496 | 2.9726 | 3.6133 | LSBoost | 57 | 0.0016067 | 6 | | 3 | Accept | 2.9975 | 0.58514 | 2.9726 | 2.9852 | Bag | 32 | - | 2 | | 4 | Accept | 4.1897 | 0.81176 | 2.9726 | 2.972 | Bag | 55 | - | 40 | | 5 | Accept | 6.3321 | 1.1966 | 2.9726 | 2.9715 | LSBoost | 55 | 0.001005 | 2 | | 6 | Best | 2.9714 | 0.67399 | 2.9714 | 2.9715 | Bag | 39 | - | 1 | | 7 | Best | 2.9615 | 0.90682 | 2.9615 | 2.9681 | Bag | 55 | - | 1 | | 8 | Accept | 3.017 | 0.3003 | 2.9615 | 2.98 | Bag | 17 | - | 1 | | 9 | Accept | 4.1881 | 3.4903 | 2.9615 | 2.9801 | LSBoost | 164 | 0.93989 | 50 | | 10 | Accept | 3.6972 | 0.33807 | 2.9615 | 2.98 | LSBoost | 12 | 0.99469 | 1 | | 11 | Accept | 3.3742 | 0.37026 | 2.9615 | 2.9801 | LSBoost | 15 | 0.13227 | 1 | | 12 | Accept | 4.1881 | 5.1746 | 2.9615 | 2.9799 | LSBoost | 205 | 0.083595 | 48 | | 13 | Accept | 5.0943 | 0.97022 | 2.9615 | 2.9799 | LSBoost | 48 | 0.014581 | 1 | | 14 | Accept | 5.5926 | 1.1539 | 2.9615 | 2.9796 | LSBoost | 47 | 0.010771 | 50 | | 15 | Accept | 6.39 | 0.6924 | 2.9615 | 2.9793 | LSBoost | 27 | 0.0010688 | 50 | | 16 | Accept | 3.3304 | 1.4641 | 2.9615 | 2.9793 | LSBoost | 78 | 0.32479 | 7 | | 17 | Accept | 4.6487 | 0.41867 | 2.9615 | 2.9795 | LSBoost | 17 | 0.055039 | 5 | | 18 | Accept | 3.264 | 0.30727 | 2.9615 | 2.9796 | LSBoost | 11 | 0.29878 | 1 | | 19 | Accept | 4.1904 | 0.3283 | 2.9615 | 2.9621 | LSBoost | 13 | 0.26663 | 50 | | 20 | Accept | 3.5279 | 9.3142 | 2.9615 | 2.9626 | LSBoost | 499 | 0.25522 | 1 | |===================================================================================================================================| | Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Method | NumLearningC-| LearnRate | MinLeafSize | | | result | log(1+loss) | runtime | (observed) | (estim.) | | ycles | | | |===================================================================================================================================| | 21 | Best | 2.9162 | 6.2751 | 2.9162 | 2.9178 | Bag | 423 | - | 2 | | 22 | Best | 2.9009 | 7.1086 | 2.9009 | 2.9043 | Bag | 499 | - | 3 | | 23 | Accept | 2.9064 | 7.4685 | 2.9009 | 2.9053 | Bag | 499 | - | 3 | | 24 | Accept | 2.909 | 7.1666 | 2.9009 | 2.9065 | Bag | 494 | - | 3 | | 25 | Accept | 2.9011 | 6.9749 | 2.9009 | 2.9051 | Bag | 499 | - | 3 | | 26 | Accept | 3.1863 | 0.26034 | 2.9009 | 2.9048 | LSBoost | 10 | 0.99529 | 10 | | 27 | Accept | 3.5444 | 8.7137 | 2.9009 | 2.9049 | LSBoost | 476 | 0.97599 | 5 | | 28 | Accept | 3.2334 | 0.31321 | 2.9009 | 2.9048 | LSBoost | 12 | 0.55679 | 4 | | 29 | Best | 2.8547 | 7.2372 | 2.8547 | 2.8575 | Bag | 487 | - | 5 | | 30 | Best | 2.84 | 7.2845 | 2.84 | 2.8436 | Bag | 499 | - | 6 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 116.4861 seconds
Total objective function evaluation time: 103.0359
Best observed feasible point:
Method NumLearningCycles LearnRate MinLeafSize
______ _________________ _________ ___________
Bag 499 NaN 6
Observed objective function value = 2.84
Estimated objective function value = 2.8436
Function evaluation time = 7.2845
Best estimated feasible point (according to models):
Method NumLearningCycles LearnRate MinLeafSize
______ _________________ _________ ___________
Bag 499 NaN 6
Estimated objective function value = 2.8436
Estimated function evaluation time = 7.4272
Mdl =
RegressionBaggedEnsemble
ResponseName: 'Y'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
HyperparameterOptimizationResults: [1x1 BayesianOptimization]
NumTrained: 499
Method: 'Bag'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: []
FitInfoDescription: 'None'
Regularization: []
FResample: 1
Replace: 1
UseObsForLearner: [94x499 logical]
Properties, Methods
最適化では、回帰の方式 (Bag および LSBoost)、NumLearningCycles、LSBoost の LearnRate、および木学習器の MinLeafSize に対して探索を行いました。出力は、推定交差検証損失が最小になるアンサンブル回帰です。
交差検証の使用によるアンサンブル回帰の最適化
十分な予測性能をもつブースティング回帰木のアンサンブルを作成する方法の 1 つは、交差検証を使用して決定木の複雑度レベルを調整することです。最適な複雑度レベルを求めるときに、学習率を調整して学習サイクル数の最小化も行います。
この例では、交差検証オプション (名前と値のペアの引数 'KFold') と関数 kfoldLoss を使用して、最適なパラメーターを手動で求めます。あるいは、名前と値のペアの引数 'OptimizeHyperparameters' を使用して自動的にハイパーパラメーターを最適化することもできます。アンサンブル回帰の最適化を参照してください。
carsmall データセットを読み込みます。燃費の予測子として、気筒数、気筒ごとの排気量、馬力、重量を選択します。
load carsmall
Tbl = table(Cylinders,Displacement,Horsepower,Weight,MPG);回帰木をブースティングする場合、木の深さの制御に関する既定値は次のとおりです。
MaxNumSplitsは10。5(次の場合)MinLeafSize10(次の場合)MinParentSize
最適な木の複雑度レベルを求めるため、以下を行います。
一連のアンサンブルを交差検証します。以後のアンサンブルについて、決定株 (1 つの分割) から最大 n - 1 個の分割まで木の複雑度レベルを指数的に増やします。n は標本サイズです。また、各アンサンブル学習率を 0.1 から 1 までの間で変化させます。
アンサンブルごとに交差検証の平均二乗誤差 (MSE) を推定します。
木の複雑度レベル () について、学習サイクル数に対してプロットすることにより、アンサンブルの交差検証済み累積 MSE を比較します。同じ Figure に、各学習率に対応する別々の曲線をプロットします。
MSE が最小になる曲線を選択し、対応する学習サイクルおよび学習率に注目します。
深い回帰木と切り株を交差検証します。欠損値がデータに含まれているので、代理分岐を使用します。これらの回帰木は基準として機能します。
rng(1) % For reproducibility MdlDeep = fitrtree(Tbl,'MPG','CrossVal','on','MergeLeaves','off', ... 'MinParentSize',1,'Surrogate','on'); MdlStump = fitrtree(Tbl,'MPG','MaxNumSplits',1,'CrossVal','on', ... 'Surrogate','on');
5 分割の交差検証を使用して、150 本のブースティング回帰木のアンサンブルを交差検証します。木テンプレートを使用して、以下を行います。
という数列の値を使用して分割の最大数を変化させます。m は、 が n - 1 を超えない値です。
代理分岐を有効にします。
{0.1, 0.25, 0.5, 1} という集合の各値を使用して、それぞれの学習率を調整します。
n = size(Tbl,1); m = floor(log2(n - 1)); learnRate = [0.1 0.25 0.5 1]; numLR = numel(learnRate); maxNumSplits = 2.^(0:m); numMNS = numel(maxNumSplits); numTrees = 150; Mdl = cell(numMNS,numLR); for k = 1:numLR for j = 1:numMNS t = templateTree('MaxNumSplits',maxNumSplits(j),'Surrogate','on'); Mdl{j,k} = fitrensemble(Tbl,'MPG','NumLearningCycles',numTrees, ... 'Learners',t,'KFold',5,'LearnRate',learnRate(k)); end end
各アンサンブルの交差検証済み累積 MSE を推定します。
kflAll = @(x)kfoldLoss(x,'Mode','cumulative'); errorCell = cellfun(kflAll,Mdl,'Uniform',false); error = reshape(cell2mat(errorCell),[numTrees numel(maxNumSplits) numel(learnRate)]); errorDeep = kfoldLoss(MdlDeep); errorStump = kfoldLoss(MdlStump);
アンサンブル内の木の本数が増加すると交差検証済み MSE がどのように変化するかをプロットします。同じプロットに学習率ごとの曲線をプロットし、木の複雑度レベルを変えた別のプロットをそれぞれ作成します。木の複雑度レベルからプロット対象となるサブセットを選択します。
mnsPlot = [1 round(numel(maxNumSplits)/2) numel(maxNumSplits)]; figure; for k = 1:3 subplot(2,2,k) plot(squeeze(error(:,mnsPlot(k),:)),'LineWidth',2) axis tight hold on h = gca; plot(h.XLim,[errorDeep errorDeep],'-.b','LineWidth',2) plot(h.XLim,[errorStump errorStump],'-.r','LineWidth',2) plot(h.XLim,min(min(error(:,mnsPlot(k),:))).*[1 1],'--k') h.YLim = [10 50]; xlabel('Number of trees') ylabel('Cross-validated MSE') title(sprintf('MaxNumSplits = %0.3g', maxNumSplits(mnsPlot(k)))) hold off end hL = legend([cellstr(num2str(learnRate','Learning Rate = %0.2f')); ... 'Deep Tree';'Stump';'Min. MSE']); hL.Position(1) = 0.6;
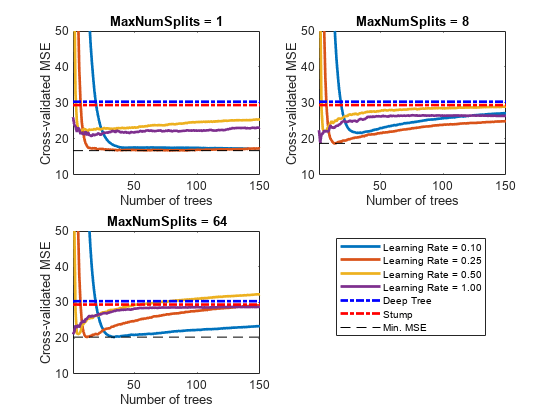
各曲線では、アンサンブル内の木の本数が最適な位置で交差検証の MSE が最小になります。
全体的に MSE が最小になる最大分割数、木の数および学習率を特定します。
[minErr,minErrIdxLin] = min(error(:));
[idxNumTrees,idxMNS,idxLR] = ind2sub(size(error),minErrIdxLin);
fprintf('\nMin. MSE = %0.5f',minErr)Min. MSE = 16.77593
fprintf('\nOptimal Parameter Values:\nNum. Trees = %d',idxNumTrees);Optimal Parameter Values: Num. Trees = 78
fprintf('\nMaxNumSplits = %d\nLearning Rate = %0.2f\n',... maxNumSplits(idxMNS),learnRate(idxLR))
MaxNumSplits = 1 Learning Rate = 0.25
最適なハイパーパラメーターおよび学習セット全体に基づいて予測アンサンブルを作成します。
tFinal = templateTree('MaxNumSplits',maxNumSplits(idxMNS),'Surrogate','on'); MdlFinal = fitrensemble(Tbl,'MPG','NumLearningCycles',idxNumTrees, ... 'Learners',tFinal,'LearnRate',learnRate(idxLR))
MdlFinal =
RegressionEnsemble
PredictorNames: {1x4 cell}
ResponseName: 'MPG'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
NumTrained: 78
Method: 'LSBoost'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [78x1 double]
FitInfoDescription: {2x1 cell}
Regularization: []
Properties, Methods
MdlFinal は RegressionEnsemble です。与えられた気筒数、全気筒の排気量、馬力、重量に対して燃費を予測するため、予測子データと MdlFinal を predict に渡すことができます。
交差検証オプション ('KFold') と関数 kfoldLoss を使用して最適な値を手動で求める代わりに、名前と値のペアの引数 'OptimizeHyperparameters' を使用できます。'OptimizeHyperparameters' を指定すると、ベイズ最適化を使用して、最適なパラメーターが自動的に求められます。'OptimizeHyperparameters' を使用して取得した最適な値は、手動で求めたものと異なる可能性があります。
t = templateTree('Surrogate','on'); mdl = fitrensemble(Tbl,'MPG','Learners',t, ... 'OptimizeHyperparameters',{'NumLearningCycles','LearnRate','MaxNumSplits'})
|====================================================================================================================| | Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | NumLearningC-| LearnRate | MaxNumSplits | | | result | log(1+loss) | runtime | (observed) | (estim.) | ycles | | | |====================================================================================================================| | 1 | Best | 3.3955 | 1.5709 | 3.3955 | 3.3955 | 26 | 0.072054 | 3 | | 2 | Accept | 6.0976 | 7.6745 | 3.3955 | 3.5549 | 170 | 0.0010295 | 70 | | 3 | Best | 3.2914 | 14.374 | 3.2914 | 3.2917 | 273 | 0.61026 | 6 | | 4 | Accept | 6.1839 | 3.5543 | 3.2914 | 3.2915 | 80 | 0.0016871 | 1 | | 5 | Best | 3.0379 | 1.0259 | 3.0379 | 3.0384 | 18 | 0.21288 | 31 | | 6 | Accept | 3.3628 | 0.8195 | 3.0379 | 3.1888 | 10 | 0.17826 | 5 | | 7 | Best | 3.0192 | 0.64526 | 3.0192 | 3.0146 | 10 | 0.27711 | 59 | | 8 | Accept | 4.0882 | 0.98266 | 3.0192 | 3.0185 | 11 | 0.11173 | 99 | | 9 | Accept | 5.762 | 0.78061 | 3.0192 | 3.0189 | 10 | 0.034877 | 3 | | 10 | Accept | 3.1248 | 1.3416 | 3.0192 | 3.0188 | 10 | 0.96615 | 2 | | 11 | Best | 2.9013 | 2.1573 | 2.9013 | 2.9012 | 49 | 0.19137 | 1 | | 12 | Accept | 2.9363 | 0.84709 | 2.9013 | 2.8984 | 14 | 0.4334 | 1 | | 13 | Accept | 3.0536 | 3.0604 | 2.9013 | 2.8996 | 64 | 0.082387 | 98 | | 14 | Accept | 3.581 | 1.5888 | 2.9013 | 2.901 | 34 | 0.98887 | 15 | | 15 | Accept | 3.0163 | 0.57988 | 2.9013 | 2.9014 | 10 | 0.46872 | 4 | | 16 | Accept | 3.0558 | 1.7569 | 2.9013 | 2.902 | 38 | 0.13318 | 13 | | 17 | Accept | 2.9378 | 1.0553 | 2.9013 | 2.9023 | 24 | 0.3038 | 1 | | 18 | Accept | 2.902 | 4.3562 | 2.9013 | 2.9019 | 104 | 0.17821 | 1 | | 19 | Accept | 2.9268 | 0.7675 | 2.9013 | 2.902 | 14 | 0.30099 | 1 | | 20 | Accept | 2.9614 | 3.1682 | 2.9013 | 2.9021 | 71 | 0.30101 | 2 | |====================================================================================================================| | Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | NumLearningC-| LearnRate | MaxNumSplits | | | result | log(1+loss) | runtime | (observed) | (estim.) | ycles | | | |====================================================================================================================| | 21 | Accept | 3.167 | 4.4952 | 2.9013 | 2.9036 | 69 | 0.19565 | 27 | | 22 | Accept | 2.9243 | 3.5797 | 2.9013 | 2.9078 | 86 | 0.064764 | 1 | | 23 | Accept | 2.9343 | 2.4519 | 2.9013 | 2.9109 | 58 | 0.094216 | 1 | | 24 | Accept | 2.9325 | 2.0003 | 2.9013 | 2.9024 | 25 | 0.22177 | 1 | | 25 | Best | 2.8958 | 8.6319 | 2.8958 | 2.8958 | 222 | 0.095888 | 1 | | 26 | Accept | 2.9224 | 7.9968 | 2.8958 | 2.8959 | 213 | 0.2378 | 1 | | 27 | Accept | 3.0618 | 6.5337 | 2.8958 | 2.8959 | 165 | 0.037531 | 99 | | 28 | Accept | 3.1105 | 0.82852 | 2.8958 | 2.9095 | 14 | 0.38101 | 47 | | 29 | Best | 2.8926 | 0.54951 | 2.8926 | 2.9032 | 11 | 0.32723 | 1 | | 30 | Accept | 2.9032 | 0.694 | 2.8926 | 2.9018 | 10 | 0.34846 | 1 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 118.3977 seconds
Total objective function evaluation time: 89.8687
Best observed feasible point:
NumLearningCycles LearnRate MaxNumSplits
_________________ _________ ____________
11 0.32723 1
Observed objective function value = 2.8926
Estimated objective function value = 2.9018
Function evaluation time = 0.54951
Best estimated feasible point (according to models):
NumLearningCycles LearnRate MaxNumSplits
_________________ _________ ____________
11 0.32723 1
Estimated objective function value = 2.9018
Estimated function evaluation time = 0.78254
mdl =
RegressionEnsemble
PredictorNames: {1x4 cell}
ResponseName: 'MPG'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
HyperparameterOptimizationResults: [1x1 BayesianOptimization]
NumTrained: 11
Method: 'LSBoost'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [11x1 double]
FitInfoDescription: {2x1 cell}
Regularization: []
Properties, Methods
入力引数
出力引数
ヒント
NumLearningCyclesは数十から数千までさまざまな数になります。通常、予測力が高いアンサンブルでは数百から数千の弱学習器が必要です。しかし、このような多数のサイクルの学習をアンサンブルが一度に行う必要はありません。数十個の学習器の学習から開始してアンサンブルの性能を調査し、必要な場合はresumeを使用して弱学習器の数を増やすことができます。アンサンブルの性能は、アンサンブルの設定と弱学習器の設定によって決まります。つまり、既定のパラメーターを使用する弱学習器を指定すると、アンサンブルの性能が低下する可能性があります。このため、アンサンブルの設定と同じように、テンプレートを使用して弱学習器のパラメーターを調整し、汎化誤差が最小になる値を選択することをお勧めします。
Resampleを使用してリサンプリングを指定する場合は、データセット全体に対してのリサンプリングをお勧めします。つまり、FResampleの既定設定である1を使用します。モデルに学習をさせた後で、新しいデータについて応答を予測する C/C++ コードを生成できます。C/C++ コードの生成には MATLAB Coder™ が必要です。詳細については、コード生成の紹介を参照してください。
アルゴリズム
アンサンブル集約アルゴリズムの詳細については、アンサンブル アルゴリズムを参照してください。
'Method','LSBoost'を指定した場合、既定では浅い決定木が成長します。木の深さは、templateTreeを使用して名前と値のペアの引数MaxNumSplits、MinLeafSizeおよびMinParentSizeを指定することにより調整できます。デュアルコア以上のシステムの場合、
fitrensembleでは Intel スレッディング ビルディング ブロック (TBB) を使用して学習を並列化します。Intel TBB の詳細については、https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.htmlを参照してください。
参照
[1] Breiman, L. “Bagging Predictors.” Machine Learning. Vol. 26, pp. 123–140, 1996.
[2] Breiman, L. “Random Forests.” Machine Learning. Vol. 45, pp. 5–32, 2001.
[3] Freund, Y. and R. E. Schapire. “A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting.” J. of Computer and System Sciences, Vol. 55, pp. 119–139, 1997.
[4] Friedman, J. “Greedy function approximation: A gradient boosting machine.” Annals of Statistics, Vol. 29, No. 5, pp. 1189–1232, 2001.
[5] Hastie, T., R. Tibshirani, and J. Friedman. The Elements of Statistical Learning section edition, Springer, New York, 2008.
拡張機能
バージョン履歴
R2016b で導入
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)