最新のリリースでは、このページがまだ翻訳されていません。 このページの最新版は英語でご覧になれます。

templateTree

決定木テンプレートの作成

構文

t = templateTree

t = templateTree(Name,Value)

説明

t = templateTree は、アンサンブル (ブースティングおよびバギングされた決定木) または誤り訂正出力符号 (ECOC) マルチクラス モデルの学習に適した、既定の決定木学習器テンプレートを返します。以下を使用する学習器として t を指定します。

• アンサンブル分類の場合は fitcensemble

• アンサンブル回帰の場合は fitrensemble

• ECOC モデル分類の場合は fitcecoc

既定の決定木テンプレートを指定する場合、学習中にすべての入力引数の既定値が使用されます。決定木の型を指定することをお勧めします。たとえば分類木テンプレートには'Type','classification' を指定します。決定木の型を指定し、コマンド ウィンドウに t を表示する場合、Type を除くすべてのオプションは空 ([]) で表示されます。

t = templateTree(Name,Value) は、1 つ以上の名前と値のペアの引数で指定された追加オプションによりテンプレートを作成します。

たとえば、カテゴリカル予測子での最適な分割を検出するためのアルゴリズム、分割基準、分割ごとに選択する予測子の数などを指定できます。

コマンド ウィンドウに t を表示する場合、すべてのオプションは、名前と値のペア引数を使用して指定する場合を除き、空 ([]) で表示されます。学習中、空のオプションに既定値が使用されます。

例

代理分岐による分類テンプレートの作成

代理分岐により決定木テンプレートを作成し、このテンプレートを使用して標本データによるアンサンブル学習を実行します。

フィッシャーのアヤメのデータセットを読み込みます。

load fisheriris

代理分岐を使用する木の切り株の決定木テンプレートを作成します。

t = templateTree('Surrogate','on','MaxNumSplits',1)

t = 
Fit template for Tree.
       Surrogate: 'on'
    MaxNumSplits: 1

テンプレート オブジェクトのオプションは、Surrogate と MaxNumSplits 以外は空です。t を学習関数に渡す場合、空のオプションはそれぞれの既定値で入力されます。

t をアンサンブル分類の弱学習器として指定します。

Mdl = fitcensemble(meas,species,'Method','AdaBoostM2','Learners',t)

Mdl = 
  classreg.learning.classif.ClassificationEnsemble
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: {'setosa'  'versicolor'  'virginica'}
           ScoreTransform: 'none'
          NumObservations: 150
               NumTrained: 100
                   Method: 'AdaBoostM2'
             LearnerNames: {'Tree'}
     ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
                  FitInfo: [100x1 double]
       FitInfoDescription: {2x1 cell}


  Properties, Methods

標本内 (再代入) 誤分類誤差を表示します。

L = resubLoss(Mdl)

L = 0.0333

交差検証の使用によるアンサンブル回帰の最適化

十分な予測性能をもつブースティングされた回帰木のアンサンブルを作成する方法の 1 つは、交差検証を使用して決定木の複雑度レベルを調整することです。最適な複雑度レベルを求めるときに、学習率を調整して学習サイクル数の最小化も行います。

この例では、交差検証オプション (名前と値のペアの引数 'KFold') と関数 kfoldLoss を使用して、最適なパラメーターを手動で求めます。あるいは、名前と値のペアの引数 'OptimizeHyperparameters' を使用して自動的にハイパーパラメーターを最適化することもできます。アンサンブル回帰の最適化を参照してください。

carsmall データセットを読み込みます。燃費の予測子として、気筒数、気筒ごとの排気量、馬力、重量を選択します。

load carsmall
Tbl = table(Cylinders,Displacement,Horsepower,Weight,MPG);

回帰木をブースティングする場合、木の深さの制御に関する既定値は次のとおりです。

• MaxNumSplits は 10。

• 5 (次の場合) MinLeafSize

• 10 (次の場合) MinParentSize

最適な木の複雑度レベルを求めるため、以下を行います。

1. 一連のアンサンブルを交差検証します。以後のアンサンブルについて、決定株 (1 つの分割) から最大 n - 1 個の分割まで木の複雑度レベルを指数的に増やします。n は標本サイズです。また、各アンサンブル学習率を 0.1 から 1 までの間で変化させます。

2. アンサンブルごとに交差検証の平均二乗誤差 (MSE) を推定します。

3. 木の複雑度レベル $$j$$ ($$j=1...J$$) について、学習サイクル数に対してプロットすることにより、アンサンブルの交差検証済み累積 MSE を比較します。同じ Figure に、各学習率に対応する別々の曲線をプロットします。

4. MSE が最小になる曲線を選択し、対応する学習サイクルおよび学習率に注目します。

深い回帰木と切り株を交差検証します。欠損値がデータに含まれているので、代理分岐を使用します。これらの回帰木は基準として機能します。

rng(1) % For reproducibility
MdlDeep = fitrtree(Tbl,'MPG','CrossVal','on','MergeLeaves','off', ...
    'MinParentSize',1,'Surrogate','on');
MdlStump = fitrtree(Tbl,'MPG','MaxNumSplits',1,'CrossVal','on', ...
    'Surrogate','on');

5 分割の交差検証を使用して、150 本のブースティングされた回帰木のアンサンブルを交差検証します。木テンプレートを使用して、以下を行います。

• $$\{2^0,2^1,...,2^m\}$$ という数列の値を使用して分割の最大数を変化させます。m は、$$2^m$$ が n - 1 を超えない値です。

• 代理分岐を有効にします。

{0.1, 0.25, 0.5, 1} という集合の各値を使用して、それぞれの学習率を調整します。

n = size(Tbl,1);
m = floor(log2(n - 1));
learnRate = [0.1 0.25 0.5 1];
numLR = numel(learnRate);
maxNumSplits = 2.^(0:m);
numMNS = numel(maxNumSplits);
numTrees = 150;
Mdl = cell(numMNS,numLR);

for k = 1:numLR
    for j = 1:numMNS
        t = templateTree('MaxNumSplits',maxNumSplits(j),'Surrogate','on');
        Mdl{j,k} = fitrensemble(Tbl,'MPG','NumLearningCycles',numTrees, ...
            'Learners',t,'KFold',5,'LearnRate',learnRate(k));
    end
end

各アンサンブルの交差検証済み累積 MSE を推定します。

kflAll = @(x)kfoldLoss(x,'Mode','cumulative');
errorCell = cellfun(kflAll,Mdl,'Uniform',false);
error = reshape(cell2mat(errorCell),[numTrees numel(maxNumSplits) numel(learnRate)]);
errorDeep = kfoldLoss(MdlDeep);
errorStump = kfoldLoss(MdlStump);

アンサンブル内の木の本数が増加すると交差検証済み MSE がどのように変化するかをプロットします。同じプロットに学習率ごとの曲線をプロットし、木の複雑度レベルを変えた別のプロットをそれぞれ作成します。木の複雑度レベルからプロット対象となるサブセットを選択します。

mnsPlot = [1 round(numel(maxNumSplits)/2) numel(maxNumSplits)];
figure;
for k = 1:3
    subplot(2,2,k)
    plot(squeeze(error(:,mnsPlot(k),:)),'LineWidth',2)
    axis tight
    hold on
    h = gca;
    plot(h.XLim,[errorDeep errorDeep],'-.b','LineWidth',2)
    plot(h.XLim,[errorStump errorStump],'-.r','LineWidth',2)
    plot(h.XLim,min(min(error(:,mnsPlot(k),:))).*[1 1],'--k')
    h.YLim = [10 50];    
    xlabel('Number of trees')
    ylabel('Cross-validated MSE')
    title(sprintf('MaxNumSplits = %0.3g', maxNumSplits(mnsPlot(k))))
    hold off
end
hL = legend([cellstr(num2str(learnRate','Learning Rate = %0.2f')); ...
        'Deep Tree';'Stump';'Min. MSE']);
hL.Position(1) = 0.6;

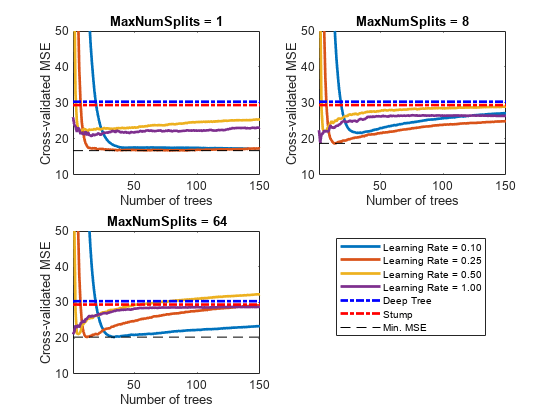
各曲線では、アンサンブル内の木の本数が最適な位置で交差検証の MSE が最小になります。

全体的に MSE が最小になる最大分割数、木の数および学習率を特定します。

[minErr,minErrIdxLin] = min(error(:));
[idxNumTrees,idxMNS,idxLR] = ind2sub(size(error),minErrIdxLin);
fprintf('\nMin. MSE = %0.5f',minErr)

Min. MSE = 17.01148

fprintf('\nOptimal Parameter Values:\nNum. Trees = %d',idxNumTrees);

Optimal Parameter Values:
Num. Trees = 38

fprintf('\nMaxNumSplits = %d\nLearning Rate = %0.2f\n',...
    maxNumSplits(idxMNS),learnRate(idxLR))

MaxNumSplits = 4
Learning Rate = 0.10

最適なハイパーパラメーターおよび学習セット全体に基づいて予測アンサンブルを作成します。

tFinal = templateTree('MaxNumSplits',maxNumSplits(idxMNS),'Surrogate','on');
MdlFinal = fitrensemble(Tbl,'MPG','NumLearningCycles',idxNumTrees, ...
    'Learners',tFinal,'LearnRate',learnRate(idxLR))

MdlFinal = 
  classreg.learning.regr.RegressionEnsemble
           PredictorNames: {'Cylinders'  'Displacement'  'Horsepower'  'Weight'}
             ResponseName: 'MPG'
    CategoricalPredictors: []
        ResponseTransform: 'none'
          NumObservations: 94
               NumTrained: 38
                   Method: 'LSBoost'
             LearnerNames: {'Tree'}
     ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
                  FitInfo: [38×1 double]
       FitInfoDescription: {2×1 cell}
           Regularization: []


  Properties, Methods

MdlFinal は RegressionEnsemble です。与えられた気筒数、全気筒の排気量、馬力、重量に対して燃費を予測するため、予測子データと MdlFinal を predict に渡すことができます。

交差検証オプション ('KFold') と関数 kfoldLoss を使用して最適な値を手動で求める代わりに、名前と値のペアの引数 'OptimizeHyperparameters' を使用できます。'OptimizeHyperparameters' を指定すると、ベイズ最適化を使用して、最適なパラメーターが自動的に求められます。'OptimizeHyperparameters' を使用して取得した最適な値は、手動で求めたものと異なる可能性があります。

t = templateTree('Surrogate','on');
mdl = fitrensemble(Tbl,'MPG','Learners',t, ...
    'OptimizeHyperparameters',{'NumLearningCycles','LearnRate','MaxNumSplits'})

|====================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | NumLearningC-|    LearnRate | MaxNumSplits |
|      | result |             | runtime     | (observed)  | (estim.)    | ycles        |              |              |
|====================================================================================================================|
|    1 | Best   |      3.3989 |       0.702 |      3.3989 |      3.3989 |           26 |     0.072054 |            3 |
|    2 | Accept |      6.0978 |      4.5175 |      3.3989 |      3.5582 |          170 |    0.0010295 |           70 |
|    3 | Best   |      3.2848 |      7.3601 |      3.2848 |       3.285 |          273 |      0.61026 |            6 |
|    4 | Accept |      6.1839 |      1.9371 |      3.2848 |      3.2849 |           80 |    0.0016871 |            1 |
|    5 | Best   |      3.0154 |     0.33314 |      3.0154 |       3.016 |           12 |      0.21457 |            2 |
|    6 | Accept |      3.3146 |     0.32962 |      3.0154 |        3.16 |           10 |      0.18164 |            8 |
|    7 | Accept |      3.0512 |     0.31776 |      3.0154 |      3.1213 |           10 |      0.26719 |           16 |
|    8 | Best   |      3.0013 |     0.29751 |      3.0013 |      3.0891 |           10 |      0.27408 |            1 |
|    9 | Best   |      2.9797 |     0.31657 |      2.9797 |      2.9876 |           10 |      0.28184 |            2 |
|   10 | Accept |      3.0646 |     0.59906 |      2.9797 |      3.0285 |           23 |       0.9922 |            1 |
|   11 | Accept |      2.9825 |     0.31056 |      2.9797 |       2.978 |           10 |      0.54187 |            1 |
|   12 | Best   |      2.9526 |     0.31189 |      2.9526 |      2.9509 |           10 |      0.49116 |            1 |
|   13 | Best   |      2.9281 |     0.98544 |      2.9281 |      2.9539 |           38 |      0.30709 |            1 |
|   14 | Accept |       2.944 |     0.60449 |      2.9281 |      2.9305 |           20 |      0.40583 |            1 |
|   15 | Best   |      2.9128 |     0.50753 |      2.9128 |      2.9237 |           20 |      0.39672 |            1 |
|   16 | Best   |      2.9077 |     0.58614 |      2.9077 |       2.919 |           21 |      0.38157 |            1 |
|   17 | Accept |      3.3932 |     0.36691 |      2.9077 |       2.919 |           10 |      0.97862 |           99 |
|   18 | Accept |      6.2938 |     0.33318 |      2.9077 |      2.9204 |           10 |    0.0074886 |           95 |
|   19 | Accept |      3.0049 |      0.4842 |      2.9077 |      2.9114 |           15 |      0.45073 |            9 |
|   20 | Best   |      2.9072 |      2.2091 |      2.9072 |      2.9111 |           87 |        0.152 |            1 |
|====================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | NumLearningC-|    LearnRate | MaxNumSplits |
|      | result |             | runtime     | (observed)  | (estim.)    | ycles        |              |              |
|====================================================================================================================|
|   21 | Accept |      2.9217 |     0.53329 |      2.9072 |      2.9154 |           21 |      0.31845 |            1 |
|   22 | Best   |      2.8994 |      4.8548 |      2.8994 |       2.917 |          189 |     0.098534 |            1 |
|   23 | Accept |      2.9055 |      7.6922 |      2.8994 |      2.9166 |          310 |      0.15505 |            1 |
|   24 | Accept |      2.9264 |      1.4456 |      2.8994 |      2.9012 |           61 |      0.23387 |            1 |
|   25 | Accept |      3.0869 |     0.34623 |      2.8994 |      2.9169 |           10 |      0.48674 |           27 |
|   26 | Best   |      2.8942 |      7.7285 |      2.8942 |      2.8912 |          319 |      0.11093 |            1 |
|   27 | Accept |      3.0175 |     0.97891 |      2.8942 |      2.8889 |           38 |      0.32187 |            4 |
|   28 | Accept |      2.9049 |      3.4053 |      2.8942 |      2.8941 |          141 |      0.13325 |            1 |
|   29 | Accept |      3.0477 |     0.30373 |      2.8942 |      2.8939 |           10 |      0.28155 |           97 |
|   30 | Accept |      3.0563 |      0.3135 |      2.8942 |       2.894 |           10 |      0.53101 |            3 |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 91.847 seconds.
Total objective function evaluation time: 51.012

Best observed feasible point:
    NumLearningCycles    LearnRate    MaxNumSplits
    _________________    _________    ____________

           319            0.11093          1      

Observed objective function value = 2.8942
Estimated objective function value = 2.894
Function evaluation time = 7.7285

Best estimated feasible point (according to models):
    NumLearningCycles    LearnRate    MaxNumSplits
    _________________    _________    ____________

           319            0.11093          1      

Estimated objective function value = 2.894
Estimated function evaluation time = 7.9767

mdl = 
  classreg.learning.regr.RegressionEnsemble
                       PredictorNames: {'Cylinders'  'Displacement'  'Horsepower'  'Weight'}
                         ResponseName: 'MPG'
                CategoricalPredictors: []
                    ResponseTransform: 'none'
                      NumObservations: 94
    HyperparameterOptimizationResults: [1×1 BayesianOptimization]
                           NumTrained: 319
                               Method: 'LSBoost'
                         LearnerNames: {'Tree'}
                 ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
                              FitInfo: [319×1 double]
                   FitInfoDescription: {2×1 cell}
                       Regularization: []


  Properties, Methods

並列計算の使用による予測子の重要度の不偏推定

carsmall データセットを読み込みます。与えられた加速、気筒数、エンジン排気量、馬力、製造業者、モデル年および重量に対して自動車の燃費の平均を予測するモデルを考えます。Cylinders、Mfg および Model_Year はカテゴリカル変数であるとします。

load carsmall
Cylinders = categorical(Cylinders);
Mfg = categorical(cellstr(Mfg));
Model_Year = categorical(Model_Year);
X = table(Acceleration,Cylinders,Displacement,Horsepower,Mfg,...
    Model_Year,Weight,MPG);

カテゴリカル変数で表現されるカテゴリの個数を表示します。

numCylinders = numel(categories(Cylinders))

numCylinders = 3

numMfg = numel(categories(Mfg))

numMfg = 28

numModelYear = numel(categories(Model_Year))

numModelYear = 3

Cylinders と Model_Year には 3 つしかカテゴリがないので、予測子分割アルゴリズムの標準 CART ではこの 2 つの変数よりも連続予測子が分割されます。

データセット全体を使用して、500 本の回帰木のランダム フォレストに学習をさせます。偏りの無い木を成長させるため、予測子の分割に曲率検定を使用するよう指定します。データには欠損値が含まれているので、代理分岐を使用するよう指定します。無作為な予測子の選択を再現するため、rng を使用して乱数発生器のシードを設定し、'Reproducible',true を指定します。

rng('default'); % For reproducibility
t = templateTree('PredictorSelection','curvature','Surrogate','on', ...
    'Reproducible',true); % For reproducibility of random predictor selections
Mdl = fitrensemble(X,'MPG','Method','bag','NumLearningCycles',500, ...
    'Learners',t);

out-of-bag 観測値を並べ替えることにより、予測子の重要度の尺度を推定します。並列計算を実行します。

options = statset('UseParallel',true);
imp = oobPermutedPredictorImportance(Mdl,'Options',options);

Starting parallel pool (parpool) using the 'local' profile ...
Connected to the parallel pool (number of workers: 6).

棒グラフを使用して推定を比較します。

figure;
bar(imp);
title('Out-of-Bag Permuted Predictor Importance Estimates');
ylabel('Estimates');
xlabel('Predictors');
h = gca;
h.XTickLabel = Mdl.PredictorNames;
h.XTickLabelRotation = 45;
h.TickLabelInterpreter = 'none';

このケースでは、最も重要な予測子は Model_Year であり、次に重要なのは Cylinders です。これらの結果を予測子の重要度の推定の結果と比較します。

ECOC マルチクラス学習のアンサンブル テンプレートの作成

fitcecocで使用するためのアンサンブル テンプレートを作成します。

不整脈データセットを読み込みます。

load arrhythmia
tabulate(categorical(Y));

  Value    Count   Percent
      1      245     54.20%
      2       44      9.73%
      3       15      3.32%
      4       15      3.32%
      5       13      2.88%
      6       25      5.53%
      7        3      0.66%
      8        2      0.44%
      9        9      1.99%
     10       50     11.06%
     14        4      0.88%
     15        5      1.11%
     16       22      4.87%

rng(1); % For reproducibility

一部のクラスでは、データ内の相対的頻度が小さいです。

分類木の AdaBoostM1 アンサンブルに対するテンプレートを作成し、100 個の学習器および 0.1 という縮小を使用するよう指定します。既定の設定では、ブースティングは切り株 (たとえば葉のセットをもつ 1 つのノード) を成長させます。頻度の小さいクラスがあるので、少数のクラスが十分な感度をもつように、ツリーのリーフ数を多くしなければなりません。葉ノードの観測値の最小数を 3 に指定します。

tTree = templateTree('MinLeafSize',20);
t = templateEnsemble('AdaBoostM1',100,tTree,'LearnRate',0.1);

Method と Type および関数呼び出し内の名前と値のペア引数の対応するプロパティを除き、テンプレート オブジェクトのすべてのプロパティは空です。t を学習関数に渡す場合、空のプロパティはそれぞれの既定値で入力されます。

t を ECOC マルチクラス モデルのバイナリ学習器として指定します。既定の 1 対 1 の 符号化設計を使用して学習させます。

Mdl = fitcecoc(X,Y,'Learners',t);

• Mdl は ClassificationECOC マルチクラス モデルです。

• Mdl.BinaryLearners は CompactClassificationEnsemble モデルの 78 行 1 列の cell 配列です。

• Mdl.BinaryLearners{j}.Trained は、j = 1,...,78 の場合に CompactClassificationTree モデルの 100 行 1 列の cell 配列です。

view を使用して、バイナリ学習器のいずれかが、切り株ではない弱学習器を含むことを検証できます。

view(Mdl.BinaryLearners{1}.Trained{1},'Mode','graph')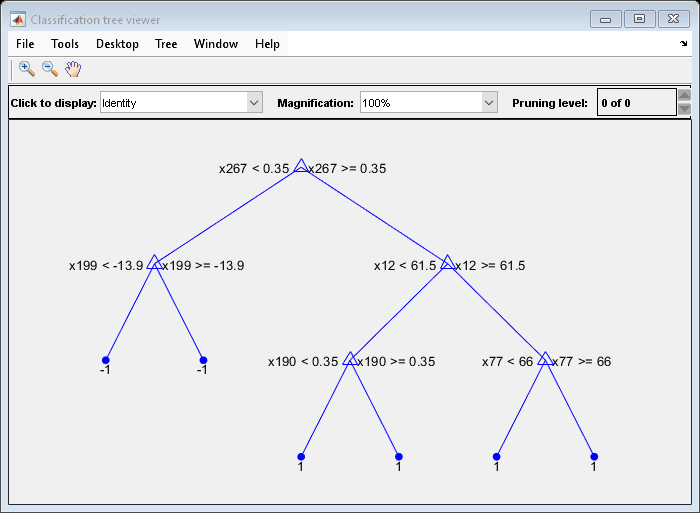

標本内 (再代入) 誤分類誤差を表示します。

L = resubLoss(Mdl,'LossFun','classiferror')

L = 0.0575

入力引数

名前と値のペアの引数

オプションの Name,Value 引数のコンマ区切りペアを指定します。Name は引数名で、Value は対応する値です。Name は引用符で囲まなければなりません。Name1,Value1,...,NameN,ValueN のように、複数の名前と値のペアの引数を、任意の順番で指定できます。

例: 'Surrogate','on','NumVariablesToSample','all' は代理分岐によるテンプレートを指定し、各分割で使用可能なすべての予測子を使用します。

分類木と回帰木

'MaxNumSplits' — 決定分岐の最大数

正の整数

木ごとの決定分岐 (枝ノード) の最大数。'MaxNumSplits' と正の整数をコンマ区切りのペアとして指定します。templateTree では、枝ノードの数が MaxNumSplits 以下になるように分割します。分割の動作についての詳細は、アルゴリズムを参照してください。

ECOC モデルの決定木バイナリ学習器とバギングされた決定木の場合、既定値は n – 1 です。n は学習標本内の観測値の個数です。ブースティングされた決定木の場合、既定値は 10 です。

例: 'MaxNumSplits',5

データ型: single | double

'MergeLeaves' — 葉マージ フラグ

'off' | 'on'

葉マージ フラグ。'MergeLeaves' と 'on' または 'off' のいずれかで構成されるコンマ区切りのペアとして指定します。

値が 'on' の場合、決定木は同じ親ノードから派生した葉をマージし、その親ノードに関連するリスク以上のリスク値の総和を与えます。'off' の場合、決定木は葉をマージしません。

ブースティングおよびバギングされた決定木の場合、既定値は 'off' です。ECOC モデルの決定木バイナリ学習器の場合、既定値は 'on' です。

例: 'MergeLeaves','on'

'MinLeafSize' — 葉ごとの観測値の最小数

正の整数値

葉ごとの観測値の最小数。'MinLeafSize' と正の整数値で構成されるコンマ区切りのペアとして指定します。各葉には少なくともツリー葉あたり MinLeafSize の観測値があります。MinParentSize と MinLeafSize の両方を指定した場合、決定木では葉の数が多くなる方の設定を使用します。つまり、MinParentSize = max(MinParentSize,2*MinLeafSize) です。

ブースティングされた決定木とバギングされた決定木を使用する場合、分類の既定値は 1、回帰の既定値は 5 です。ECOC モデルの決定木バイナリ学習器の場合、既定値は 1 です。

例: 'MinLeafSize',2

'MinParentSize' — 枝ノードごとの観測値の最小数

正の整数値

枝ノードごとの観測値の最小数。'MinParentSize' と正の整数値で構成されるコンマ区切りのペアとして指定します。ツリーの各枝ノードには少なくとも MinParentSize の観測値があります。MinParentSize と MinLeafSize の両方を指定した場合、決定木では葉の数が多くなる方の設定を使用します。つまり、MinParentSize = max(MinParentSize,2*MinLeafSize) です。

ブースティングされた決定木とバギングされた決定木を使用する場合、分類の既定値は 2、回帰の既定値は 10 です。ECOC モデルの決定木バイナリ学習器の場合、既定値は 10 です。

例: 'MinParentSize',4

'NumVariablesToSample' — 各分割についてランダムに選択する予測子の数

正の整数値 | 'all'

分割ごとにランダムに選択する予測子の数。'NumVariablesToSample' と正の整数値で構成されるコンマ区切りのペアとして指定します。また、'all' を指定すると、使用可能なすべての予測子が使用されます。

多数の予測子が学習データに含まれている場合に予測子の重要度を分析するには、'NumVariablesToSample' として 'all' を指定します。このようにしないと、重要度が過小評価されて一部の予測子が選択されない可能性があります。

無作為な選択を再現するには、rng を使用して乱数発生器のシードを設定し、'Reproducible',true を指定しなければなりません。

ECOC モデル内のブースティングされた決定木および決定木バイナリ学習器の場合、既定値は 'all' です。バギングされた決定木の場合の既定値は、分類については予測子の個数の平方根、回帰については予測子の個数の 3 分の 1 です。

例: 'NumVariablesToSample',3

データ型: single | double | char | string

'PredictorSelection' — 最適な分割予測子の選択に使用するアルゴリズム

'allsplits' (既定値) | 'curvature' | 'interaction-curvature'

各ノードで最適な分割予測子の選択に使用するアルゴリズム。'PredictorSelection' と次の表の値から構成されるコンマ区切りのペアとして指定します。

値	説明
'allsplits'	標準 CART — すべての予測子に対して可能なすべての分割について分割基準ゲインを最大化する分割予測子を選択します[1]。
'curvature'	曲率検定 — 各予測子と応答の間の独立性に対するカイ二乗検定の p 値を最小化する分割予測子を選択します[3][4]。学習速度は標準 CART と同等です。
'interaction-curvature'	交互作用検定 — 各予測子と応答の間の独立性に対するカイ二乗検定の p 値、および予測子の各ペアと応答の間の独立性に対するカイ二乗検定の p 値を最小化する分割予測子を選択します[3]。学習速度は標準 CART より遅くなる可能性があります。

'curvature' と 'interaction-curvature' では、すべての検定で p 値が 0.05 を超える場合、MATLAB^® はノードの分割を停止します。

ヒント

• 決定木をブースティングする場合、曲率検定と交互作用検定は推奨されません。精度が高いブースティングされた木のアンサンブルに学習をさせるには、代わりに標準 CART を使用してください。

• 標準 CART アルゴリズムには、相違する値が少ない分割予測子 (カテゴリカル変数など) よりも、相違する値が多い分割予測子 (連続変数など) を選択する傾向があります[4]。予測子データセットが異種混合である場合や、一部の予測子が相違する値を他の変数よりも相対的に少なく含んでいる場合は、曲率検定または交互作用検定の指定を検討してください。

  • 相違する値の個数が他の予測子よりも比較的少ない予測子がある場合 (予測子データセットが異種混合である場合など)。

  • 予測子の重要度の分析が目標である場合。予測子の重要度の推定に関する詳細については、分類問題の場合は oobPermutedPredictorImportance を、回帰問題の場合は oobPermutedPredictorImportance を参照してください。

• 標準 CART を使用して成長させた木は、予測子変数の交互作用の影響を受けません。また、多くの無関係な予測子が存在する状況では、このような木によって重要な変数が特定される可能性は、交互作用検定を適用した場合より低くなります。このため、予測子の交互作用を考慮し、重要度変数の特定を多くの無関係な変数が存在する状況で行うには、交互作用検定を指定します[3]。

• 'PredictorSelection' の値は、予測速度に影響を与えません。

templateTree が分割予測子を選択する方法の詳細については、ノード分割規則(分類)、ノード分割規則(回帰) および分割予測子選択手法の選択を参照してください。

例: 'PredictorSelection','curvature'

'Prune' — 枝刈りされた部分木の最適シーケンスを推定するフラグ

'off' | 'on'

枝刈りされた部分木の最適なシーケンスを推定するフラグ。'Prune' と 'on' または 'off' で構成されるコンマ区切りのペアとして指定します。

Prune が 'on' の場合、分類木学習器の学習で枝刈りは行われませんが、ECOC モデルの決定木バイナリ アンサンブルまたはアンサンブルの学習器のそれぞれに対して、枝刈りした部分木の最適シーケンスが推定されます。それ以外の場合、分類木学習器の学習では、枝刈りした部分木の最適シーケンスが推定されません。

ブースティングおよびバギングされた決定木の場合、既定値は 'off' です。

ECOC モデルの決定木バイナリ学習器の場合、既定値は 'on' です。

例: 'Prune','on'

'PruneCriterion' — 枝刈り条件

'error' | 'impurity' | 'mse'

枝刈り条件。'PruneCriterion' と木のタイプに対して有効な枝刈り条件から構成されるコンマ区切りのペアとして指定します。

• 分類木の場合、'error' (既定の設定) または 'impurity' を指定できます。'impurity' を指定した場合、templateTree は名前と値のペアの引数 'SplitCriterion' によって指定された不純度の尺度を使用します。

• 回帰木の場合、'mse' (既定値) のみを指定できます。

例: 'PruneCriterion','impurity'

'Reproducible' — 再現性を強制するためのフラグ

false (logical 0) (既定値) | true (logical 1)

モデルの学習の反復実行における再現性を強制するためのフラグ。'Reproducible' と false または true から構成されるコンマ区切りのペアとして指定します。

'NumVariablesToSample' が 'all' ではない場合、各分岐で予測子が無作為に選択されます。無作為な選択を再現するには、'Reproducible',true を指定し、rng を使用して乱数発生器のシードを設定しなければなりません。'Reproducible' を true に設定すると学習速度が低下する可能性があることに注意してください。

例: 'Reproducible',true

データ型: logical

'SplitCriterion' — 分割条件

'gdi' | 'twoing' | 'deviance' | 'mse'

分割条件。'SplitCriterion' と木のタイプに対して有効な分割条件から構成されるコンマ区切りのペアとして指定します。

• 分類木の場合、次のようになります。

  • ジニ多様性指数の場合は 'gdi' (既定の設定)

  • twoing 規則の場合は 'twoing'

  • 最大逸脱度減少量 (クロス エントロピー) の場合は 'deviance'

• 回帰木の場合、次のようになります。

  • 平均二乗誤差の場合は 'mse' (既定の設定)

例: 'SplitCriterion','deviance'

'Surrogate' — 代理決定分岐

'off' (既定値) | 'on' | 'all' | 正の整数値

代理決定分岐フラグ。'Surrogate' と、'off'、'on'、'all' または正の整数で構成される、コンマ区切りのペアとして指定します。

• 'off' に設定すると、決定木は枝ノードで代理分岐を検出しません。

• 'on' に設定すると、決定木は各枝ノードで最大 10 個の代理分岐を検出します。

• 'all' に設定すると、決定木は各枝ノードですべての代理分岐を検出します。'all' に設定すると、処理時間およびメモリ消費量が非常に増加する可能性があります。

• 正の整数値に設定すると、決定木は各枝ノードで最大で指定された数の代理分岐を探します。

代理分岐を使用すると、欠損値をもつデータの予測精度が改善されます。また、予測子同士の関連性予測尺度も計算できます。

例: 'Surrogate','on'

データ型: single | double | char | string

分類木の場合のみ、次のようになります。

'AlgorithmForCategorical' — 最適なカテゴリカル予測子の分割のアルゴリズム

'Exact' | 'PullLeft' | 'PCA' | 'OVAbyClass'

データの C 個のカテゴリと K (3 以上) 個のクラスをもつデータのカテゴリカル予測子での最適な分割を検索するアルゴリズム。'AlgorithmForCategorical' と次のいずれかで構成されるコンマ区切りのペアとして指定されます。

値	説明
'Exact'	2C–1 – 1 のすべての組み合わせを検討します。
'PullLeft'	右枝にあるすべての C カテゴリから開始します。残りのカテゴリにおいて K クラスの最小不純度を実現するように、各カテゴリを左枝に移動することを検討してください。このシーケンスから、最小の不純度をもつ分割を選択します。
'PCA'	(中心となるクラス確率行列の) 重み付け共分散行列の最初の主成分とそのカテゴリに対するクラス確率のベクトル間の内積を使用して、各カテゴリのスコアを計算します。スコアを昇順に並べ替え、C - 1 とおりの分割すべてを検討します。
'OVAbyClass'	右枝にあるすべての C カテゴリから開始します。クラスごとに、そのクラスの確率に基づいてカテゴリの順序を設定します。最初のクラスでは、各カテゴリを左枝に順番に移動し、各移動の不純度基準を記録します。残りのクラスに対して同じ作業を繰り返します。このシーケンスから、最小の不純度をもつ分割を選択します。

カテゴリカル予測子の既知のクラス数およびレベル数を使用して、各分割について最適なアルゴリズムのサブセットが選択されます。2 クラスの場合、常に厳密探索が実行されます。'AlgorithmForCategorical' 名前と値のペアの引数を使用して、特定のアルゴリズムを指定します。

詳細は、分類木のカテゴリカル予測子の分割を参照してください。

例: 'AlgorithmForCategorical','PCA'

'MaxNumCategories' — 分割ノードのカテゴリ レベルの最大数

10 (既定値) | 非負のスカラー値

分割ノードのカテゴリ レベルの最大数。'MaxNumCategories' と非負のスカラー値から構成されるコンマ区切りのペアとして指定します。分割ノードにおける予測子のレベル数が最大で MaxNumCategories である場合、分類木では厳密探索アルゴリズムを使用してカテゴリカル予測子が分割されます。それ以外の場合、厳密ではないアルゴリズムのいずれかを使用して最適なカテゴリカル分割が探索されます。渡す値が小さい場合、計算時間とメモリの負荷が増加することがあります。

例: 'MaxNumCategories',8

回帰木の場合のみ、次のようになります。

'QuadraticErrorTolerance' — 二次誤差の許容誤差

1e-6 (既定値) | 正のスカラー値

ノードあたりの二次誤差の許容誤差。'QuadraticErrorTolerance' と正のスカラー値で構成されるコンマ区切りのペアとして指定します。ノードあたりの重み付き平均二乗誤差が QuadraticErrorTolerance*ε より小さくなると回帰木のノード分割が停止します。ここで ε は、決定木を成長させる前に計算された、n 個の応答すべての重み付き平均二乗誤差です。

$$\epsilon ={\displaystyle \sum _{i=1}^n{w}_i{\left(y_i-\overline{y}\right)}^2}.$$

w_i は、すべての観測値の重みの合計が 1 になる ($${\displaystyle \sum _{i=1}^n{w}_i}=1$$) と仮定した場合の観測値 i の重みです。

$$\overline{y}={\displaystyle \sum _{i=1}^n{w}_i}{y}_i$$

は、すべての応答の加重平均です。

例: 'QuadraticErrorTolerance',1e-4

出力引数

t — 分類または回帰の決定木テンプレート

テンプレート オブジェクト

アンサンブル (ブースティングおよびバギンされた決定木) または誤り訂正出力符号 (ECOC) マルチクラス モデルの学習に適した、分類または回帰用の決定木テンプレート。テンプレート オブジェクトとして返します。t を fitcensemble、fitrensemble または fitcecoc に渡して、アンサンブル分類、アンサンブル回帰または ECOC モデル用の決定木をそれぞれ作成する方法を指定します。

コマンド ウィンドウで t を表示する場合、すべての未指定のオプションは空 ([]) で表示されます。しかし、空のオプションは学習中に対応する既定値に置き換えられます。

アルゴリズム

• MaxNumSplits に対応するため、現在の "レイヤー" に含まれているすべてのノードを分割してから枝ノードの数をカウントします。レイヤーとは、ルート ノードから同じ距離にあるノードの集合です。枝ノードの数が MaxNumSplits を超えた場合、以下の処理が行われます。

  1. 現在のレイヤーに含まれている枝ノード数が、最大でも MaxNumSplits になるように、分割を解除する数を判断する。

  2. 不純度順に枝ノードを並べ替える。

  3. 適切ではない分岐の分割を解除する。

  4. それまでに成長させた決定木を返す。

  この手順は、バランスが最大の木を生成することを目指しています。

• 次の条件のいずれかが満たされるまで、枝ノードをレイヤー単位で分割します。

  • MaxNumSplits + 1 個の枝ノードが存在している。

  • 推奨されている分割を行うと、少なくとも 1 つの枝ノードで観測値の数が MinParentSize より少なくなる。

  • 推奨される分割を行うと、少なくとも 1 つの葉ノードで観測値の数が MinLeafSize より少なくなる。

  • レイヤー内で適切な分割を検出できない。つまり、現在の枝刈り基準 (PruneCriterion 参照) では、レイヤー内で推奨されている分割を行っても状況が改善されない。このイベントの特殊なケースは、すべてのノードが純粋 (ノード内のすべての観測値が同じクラス) になる場合です。

  • PredictorSelection の値が 'curvature' または 'interaction-curvature' の場合に、すべての検定で p 値が 0.05 を超える。

  MaxNumSplits と MinLeafSize は、既定値で行われる分割に影響を与えません。'MaxNumSplits' を設定した場合、MaxNumSplits 回の分割が発生する前に、MinParentSize の値が原因となって分割が停止することもあります。

• 決定木を成長させるときの分割予測子の選択とノード分割アルゴリズムの詳細については、分類木の場合はアルゴリズムを、回帰木の場合はアルゴリズムを参照してください。

参照

[1] Breiman, L., J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Boca Raton, FL: CRC Press, 1984.

[2] Coppersmith, D., S. J. Hong, and J. R. M. Hosking. “Partitioning Nominal Attributes in Decision Trees.” Data Mining and Knowledge Discovery, Vol. 3, 1999, pp. 197–217.

[3] Loh, W.Y. “Regression Trees with Unbiased Variable Selection and Interaction Detection.” Statistica Sinica, Vol. 12, 2002, pp. 361–386.

[4] Loh, W.Y. and Y.S. Shih. “Split Selection Methods for Classification Trees.” Statistica Sinica, Vol. 7, 1997, pp. 815–840.

参考

ClassificationTree | RegressionTree | fitcecoc | fitcensemble | fitctree | fitrensemble | templateEnsemble

R2014a で導入

×

例を開く

この例の変更されたバージョンがシステム上にあります。代わりにこのバージョンを開きますか?

いいえ、変更されたバージョンを上書きします。 はい