回帰用の自動特徴量エンジニアリング
関数 genrfeatures では、特徴量エンジニアリング プロセスを機械学習ワークフローのコンテキストで自動化できます。表形式の学習データを回帰モデルに渡す前に、genrfeatures を使用してデータ内の予測子から新しい特徴量を作成できます。返されたデータを使用してモデルに学習させます。
新しい特徴量を機械学習ワークフローに基づいて生成します。
解釈可能な回帰モデル用の特徴量を生成するには、
genrfeaturesの呼び出しでTargetLearnerに既定値の"linear"を使用します。その後、返されたデータを使用して線形回帰モデルに学習させることができます。例については、生成された特徴量をもつ線形モデルの解釈を参照してください。モデル予測の向上につながるような特徴量を生成するには、
genrfeaturesの呼び出しでTargetLearner="bag"またはTargetLearner="gaussian-svm"を指定します。その後、返されたデータを使用してバギング アンサンブル回帰モデルまたはガウス カーネルを使用したサポート ベクター マシン (SVM) 回帰モデルに学習させることができます。例については、新しい特徴量の生成によるバギング アンサンブルの性能の向上を参照してください。
生成された特徴量について詳しく確認するには、FeatureTransformer オブジェクトの関数 describe を使用します。学習セットと同じ特徴変換をテスト セットや検証セットに適用するには、FeatureTransformer オブジェクトの関数 transform を使用します。
生成された特徴量をもつ線形モデルの解釈
自動特徴量エンジニアリングを使用して新しい特徴量を生成します。生成された特徴量を使用して線形回帰モデルに学習をさせます。生成された特徴量と学習させたモデルの関係を解釈します。
patients データ セットを読み込みます。変数のサブセットから table を作成します。テーブルの最初の数行を表示します。
load patients Tbl = table(Age,Diastolic,Gender,Height,SelfAssessedHealthStatus, ... Smoker,Weight,Systolic); head(Tbl)
Age Diastolic Gender Height SelfAssessedHealthStatus Smoker Weight Systolic
___ _________ __________ ______ ________________________ ______ ______ ________
38 93 {'Male' } 71 {'Excellent'} true 176 124
43 77 {'Male' } 69 {'Fair' } false 163 109
38 83 {'Female'} 64 {'Good' } false 131 125
40 75 {'Female'} 67 {'Fair' } false 133 117
49 80 {'Female'} 64 {'Good' } false 119 122
46 70 {'Female'} 68 {'Good' } false 142 121
33 88 {'Female'} 64 {'Good' } true 142 130
40 82 {'Male' } 68 {'Good' } false 180 115
Tbl の変数から新しい特徴量を 10 個生成します。応答として変数 Systolic を指定します。genrfeatures では、既定では新しい特徴量を線形回帰モデルの学習に使用すると見なします。
rng("default") % For reproducibility [T,NewTbl] = genrfeatures(Tbl,"Systolic",10)
T =
FeatureTransformer with properties:
Type: 'regression'
TargetLearner: 'linear'
NumEngineeredFeatures: 10
NumOriginalFeatures: 0
TotalNumFeatures: 10
NewTbl=100×11 table
zsc(d(Smoker)) q8(Age) eb8(Age) zsc(sin(Height)) zsc(kmd8) q6(Height) eb8(Diastolic) q8(Diastolic) zsc(fenc(c(SelfAssessedHealthStatus))) q10(Weight) Systolic
______________ _______ ________ ________________ _________ __________ ______________ _____________ ______________________________________ ___________ ________
1.3863 4 5 1.1483 -0.56842 6 8 8 0.27312 7 124
-0.71414 6 6 -0.3877 -2.0772 5 2 2 -1.4682 6 109
-0.71414 4 5 1.1036 -0.21519 2 4 5 0.82302 3 125
-0.71414 5 6 -1.4552 -0.32389 4 2 2 -1.4682 4 117
-0.71414 8 8 1.1036 1.2302 2 3 4 0.82302 1 122
-0.71414 7 7 -1.5163 -0.88497 4 1 1 0.82302 5 121
1.3863 3 3 1.1036 -1.1434 2 6 6 0.82302 5 130
-0.71414 5 6 -1.5163 -0.3907 4 4 5 0.82302 8 115
-0.71414 1 2 -1.5163 0.4278 4 3 3 0.27312 9 115
-0.71414 2 3 -0.26055 -0.092621 3 5 6 0.27312 3 118
-0.71414 7 7 -1.5163 0.16737 4 2 2 0.27312 2 114
-0.71414 6 6 -0.26055 -0.32104 3 1 1 -1.8348 5 115
-0.71414 1 1 1.1483 -0.051074 6 1 1 -1.8348 7 127
1.3863 5 5 0.14351 2.3695 6 8 8 0.27312 10 130
-0.71414 3 4 0.96929 0.092962 2 3 4 0.82302 3 114
1.3863 8 8 1.1483 -0.049336 6 7 8 0.82302 8 130
⋮
T は新しいデータの変換に使用できる FeatureTransformer オブジェクトで、newTbl には Tbl のデータから生成された新しい特徴量が格納されます。
生成された特徴量について詳しく確認するには、FeatureTransformer オブジェクトのオブジェクト関数 describe を使用します。たとえば、生成された最初の 2 つの特徴量を調べます。
describe(T,1:2)
Type IsOriginal InputVariables Transformations
___________ __________ ______________ ___________________________________________________________
zsc(d(Smoker)) Numeric false Smoker Variable of type double converted from an integer data type
Standardization with z-score (mean = 0.34, std = 0.4761)
q8(Age) Categorical false Age Equiprobable binning (number of bins = 8)
newTbl の 1 つ目の特徴量は数値変数で、最初に変数 Smoker の値を double 型の数値変数に変換してから、その結果を z スコアに変換して作成されています。newTbl の 2 つ目の特徴量はカテゴリカル変数で、変数 Age の値を 8 個の同確率のビンにビン化して作成されています。
生成された特徴量を使用して、正則化なしで線形回帰モデルを当てはめます。
Mdl = fitrlinear(NewTbl,"Systolic",Lambda=0);Mdl の学習に使用された予測子の係数をプロットします。fitrlinear では、モデルを当てはめる前にカテゴリカル予測子が展開されることに注意してください。
p = length(Mdl.Beta); [sortedCoefs,expandedIndex] = sort(Mdl.Beta,ComparisonMethod="abs"); sortedExpandedPreds = Mdl.ExpandedPredictorNames(expandedIndex); bar(sortedCoefs,Horizontal="on") yticks(1:2:p) yticklabels(sortedExpandedPreds(1:2:end)) xlabel("Coefficient") ylabel("Expanded Predictors") title("Coefficients for Expanded Predictors")
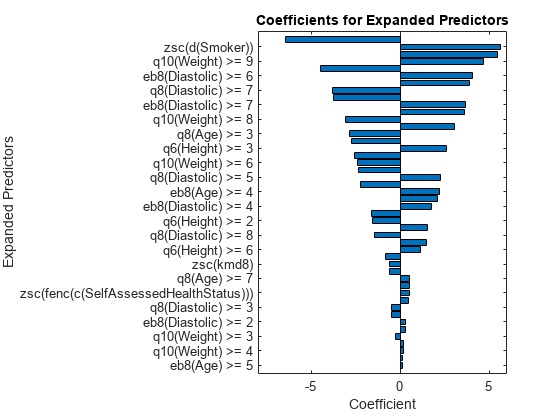
係数の絶対値が大きい予測子を特定します。
bigCoefs = abs(sortedCoefs) >= 4; flip(sortedExpandedPreds(bigCoefs))
ans = 1×6 cell
{'eb8(Diastolic) >= 5'} {'zsc(d(Smoker))'} {'q8(Age) >= 2'} {'q10(Weight) >= 9'} {'q6(Height) >= 5'} {'eb8(Diastolic) >= 6'}
部分依存プロットを使用して、絶対値に関して大きな係数をもつレベルのカテゴリカル特徴量を解析できます。たとえば、eb8(Diastolic) >= 5 と eb8(Diastolic) >= 6 のレベルで係数の絶対値が大きくなっている変数 eb8(Diastolic) の部分依存プロットを調べます。これらの 2 つのレベルは、予測した Systolic の値の目立った変化に対応します。
plotPartialDependence(Mdl,"eb8(Diastolic)",NewTbl);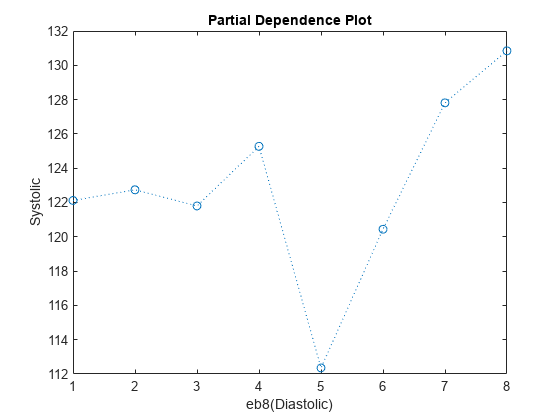
新しい特徴量の生成によるバギング アンサンブルの性能の向上
バギング アンサンブル回帰モデルに学習させる前に、genrfeatures を使用して新しい特徴量を設計します。新しいデータの予測の前に同じ特徴変換を新しいデータ セットに適用します。設計した特徴量を使用するアンサンブルのテスト セット性能と元の特徴量を使用するアンサンブルのテスト セット性能を比較します。
停電のデータをワークスペースに table として読み込みます。欠損値がある観測値を削除し、table の最初の数行を表示します。
outages = readtable("outages.csv");
Tbl = rmmissing(outages);
head(Tbl) Region OutageTime Loss Customers RestorationTime Cause
_____________ ________________ ______ __________ ________________ ___________________
{'SouthWest'} 2002-02-01 12:18 458.98 1.8202e+06 2002-02-07 16:50 {'winter storm' }
{'SouthEast'} 2003-02-07 21:15 289.4 1.4294e+05 2003-02-17 08:14 {'winter storm' }
{'West' } 2004-04-06 05:44 434.81 3.4037e+05 2004-04-06 06:10 {'equipment fault'}
{'MidWest' } 2002-03-16 06:18 186.44 2.1275e+05 2002-03-18 23:23 {'severe storm' }
{'West' } 2003-06-18 02:49 0 0 2003-06-18 10:54 {'attack' }
{'NorthEast'} 2003-07-16 16:23 239.93 49434 2003-07-17 01:12 {'fire' }
{'MidWest' } 2004-09-27 11:09 286.72 66104 2004-09-27 16:37 {'equipment fault'}
{'SouthEast'} 2004-09-05 17:48 73.387 36073 2004-09-05 20:46 {'equipment fault'}
変数の中には、OutageTime や RestorationTime など、fitrensemble のような回帰モデル学習関数でサポートされないデータ型の変数も含まれています。
データを学習セットとテスト セットに分割します。観測値の約 70% を学習データとして使用し、観測値の約 30% をテスト データとして使用します。データの分割には cvpartition を使用します。
rng("default") % For reproducibility of the partition c = cvpartition(size(Tbl,1),Holdout=0.30); TrainTbl = Tbl(training(c),:); TestTbl = Tbl(test(c),:);
学習データを使用して、バギング アンサンブルの当てはめに使用する新しい特徴量を 30 個生成します。既定では、30 個の特徴量の中にバギング アンサンブルで予測子として使用できる元の特徴量が含まれます。
[Transformer,NewTrainTbl] = genrfeatures(TrainTbl,"Loss",30, ... TargetLearner="bag"); Transformer
Transformer =
FeatureTransformer with properties:
Type: 'regression'
TargetLearner: 'bag'
NumEngineeredFeatures: 27
NumOriginalFeatures: 3
TotalNumFeatures: 30
オブジェクト Transformer に格納された変換をテスト データに適用して NewTestTbl を作成します。
NewTestTbl = transform(Transformer,TestTbl);
元の学習セット TrainTbl を使用してバギング アンサンブルに学習させ、元のテスト セット TestTbl でモデルの平均二乗誤差 (MSE) を計算します。fitrensemble が使用できる 3 つの予測子変数 (Region、Customers、および Cause) のみ指定し、2 つの datetime 予測子変数 (OutageTime および RestorationTime) を省略します。次に、変換後の学習セット NewTrainTbl を使用してバギング アンサンブルに学習させ、変換後のテスト セット NewTestTbl でモデルの MSE を計算します。
originalMdl = fitrensemble(TrainTbl,"Loss ~ Region + Customers + Cause", ... Method="bag"); originalTestMSE = loss(originalMdl,TestTbl)
originalTestMSE = 1.8999e+06
newMdl = fitrensemble(NewTrainTbl,"Loss",Method="bag"); newTestMSE = loss(newMdl,NewTestTbl)
newTestMSE = 1.8617e+06
newTestMSE が originalTestMSE より小さくなっており、変換後のデータで学習させたバギング アンサンブルの方が元のデータで学習させたバギング アンサンブルよりも性能がわずかに高くなっていることを示しています。
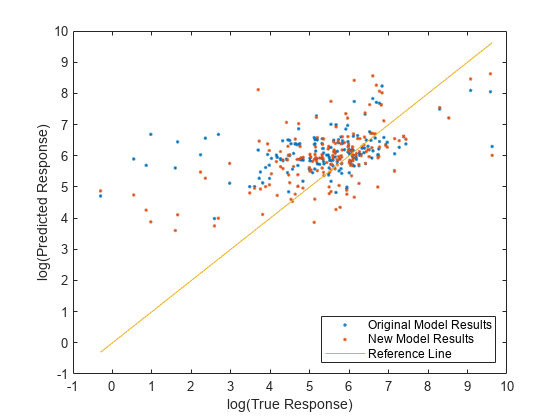
テスト セットの予測応答値と実際の応答値を両方のモデルで比較します。予測応答の対数を縦軸に、実際の応答 (Loss) の対数を横軸に沿ってプロットします。基準線上にある点は予測が正しいことを示します。優れたモデルでは、生成された予測が線の近くに分布します。
predictedTestY = predict(originalMdl,TestTbl); newPredictedTestY = predict(newMdl,NewTestTbl); plot(log(TestTbl.Loss),log(predictedTestY),".") hold on plot(log(TestTbl.Loss),log(newPredictedTestY),".") hold on plot(log(TestTbl.Loss),log(TestTbl.Loss)) hold off xlabel("log(True Response)") ylabel("log(Predicted Response)") legend(["Original Model Results","New Model Results","Reference Line"], ... Location="southeast") xlim([-1 10]) ylim([-1 10])
参考
genrfeatures | FeatureTransformer | describe | transform | fitrlinear | fitrensemble | fitrsvm | plotPartialDependence | gencfeatures