システム アルゴリズムのモデル化

ステップ 7 - 1: 基本的なモデル化のワークフロー

• 1
• 2
• 3

不完全なシステム要件や開発中のシステム設計が原因でファイル管理やモデル アーキテクチャを事前に定義できない場合でも、基本的なシステム アルゴリズムをモデル化することはできます。モデルを入力、出力、システムに整理することで、モデルの構築を進めながらモデル コンポーネントの全体的なフレームワークを作成します。

限られた情報で開始するモデリング ワークフローの第 1 ステージを示すために、この例では質量、バネ、ダンパーで構成された単純な機械システムを使用します。

次の 2 次微分方程式によってシステムが特徴付けられます。

$$\mathit{m}\ddot{\mathrm{x}}+\mathit{c}\dot{\mathrm{x}}+\mathrm{kx}=\mathit{F}$$

この方程式は、以下を意味します。

• $$m$$ は質量。

• $$c$$ は減衰係数。

• $$k$$ はバネ定数。

• $$\underset{}{\overset{¨}{x}}$$ は加速度。

• $$\underset{}{\overset{\dot{}}{x}}$$ は速度。

• $$x$$ は変位。

• $$F$$ は外力。

$$\underset{}{\overset{¨}{x}}$$ について解くと、より明確に Simulink® モデルにマッピングする次のような形式の方程式が示されます。

$$\ddot{\mathit{x}}=\frac{1}{\mathit{m}}\left(\mathit{F}-\mathit{c}\dot{\mathrm{x}}-\mathrm{kx}\right)$$

BasicModelingSimpleSystem という名前のモデルはこの方程式を表します。

mdl = "BasicModelingSimpleSystem";
open_system(mdl);

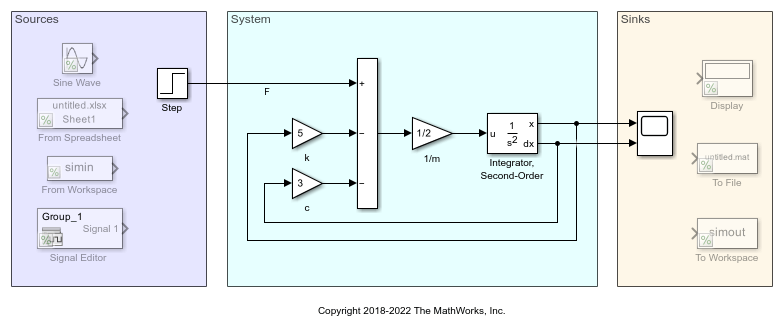
Sum ブロックは質量に働く正味の力を計算します。1/m というラベルの付いた Gain ブロックは、正味の力に $$1/m$$ を乗算して質量の加速度を計算します。Integrator, Second-Order ブロックは質量の速度と位置を解きます。

モデルでは、ブロックが次の 3 つの領域に整理されています。

• Sources という名前の領域にはシステム入力が含まれています。

• System という名前の領域にはシステムまたはプラントを表すブロックが含まれています。

• Sinks という名前の領域にはシステム出力が含まれています。

モデルを事前に整理することで、モデルの構築を進めながらモデル コンポーネントの全体的なフレームワークを作成します。

この例では、開発の予備段階でのモデルが示されているため、実際の入力の力は不明であり、さまざまな標準ソース ブロックによって表すことができます。モデルは、入力としてシステムに接続された Step ブロックを使用します。代替のソース ブロックがいくつか示されていますが、コメントアウトされています。たとえば、From Spreadsheet ブロックを使用して、使用可能な実測データを読み込むことができます。

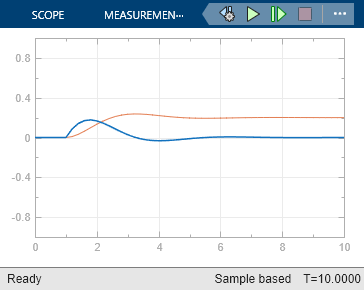
同様に、さまざまな Sink ブロックが出力の変位を受け入れることができます。シミュレーション結果が予測と一致するかどうかを確認するために、モデルは Scope ブロックを使用して信号を可視化します。

sim(mdl);

参考

トピック

• Sources
• Sinks

ステップ 7 - 1: 基本的なモデル化のワークフロー

• 1
• 2
• 3