stepz

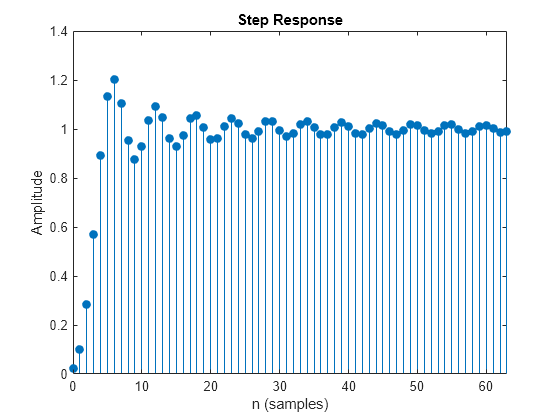
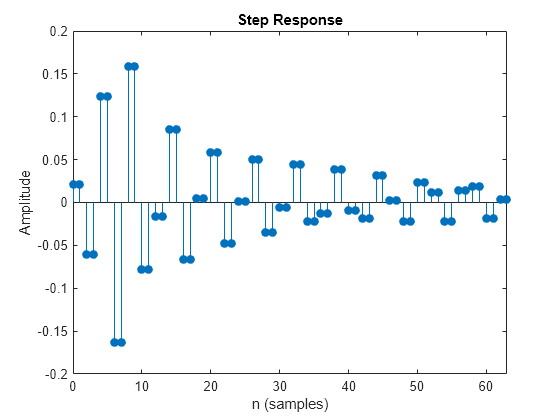
デジタル フィルターのステップ応答

構文

[h,t] = stepz(b,a)

[h,t] = stepz(B,A,"ctf")

[h,t] = stepz({B,A,g},"ctf")

[h,t] = stepz(d)

[h,t] = stepz(sos)

[h,t] = stepz(___,n)

[h,t] = stepz(___,n,fs)

stepz(___)

説明

[h,t] = stepz(b,a) は、指定されたデジタル フィルターのステップ応答を返します。分子係数 b と分母係数 a をもつデジタル フィルターを指定します。この関数は、ステップ応答ベクトルを h で返し、サンプル時間を t で返します。

[h,t] = stepz(B,A,"ctf") は、分子係数 B と分母係数 A をもつCascaded Transfer Functions (CTF) として表されるデジタル フィルターのステップ応答を返します。 (R2024b 以降)

[h,t] = stepz({B,A,g},"ctf") は、デジタル フィルターのステップ応答を CTF 形式で返します。分子係数 B、分母係数 A、およびフィルター セクション全体のスケーリング値 g を使用してフィルターを指定します。 (R2024b 以降)

[h,t] = stepz(d) では、デジタル フィルター d のステップ応答が返されます。

[h,t] = stepz(sos) では、2 次セクション行列 sos に対応するステップ応答が返されます。

[h,t] = stepz(___,n) では、ステップ応答の最初の n 個のサンプルが計算されます。この構文には、前の構文の入力引数を任意に組み合わせて含めることができます。

[h,t] = stepz(___,n,fs) では、n 個のサンプルが計算され、サンプル間隔が 1/fs 単位の間隔になるようなベクトル t が生成されます。

出力引数なしで stepz(___) を使用すると、フィルターのステップ応答がプロットされます。

例

バタワース フィルターのステップ応答

正規化された電力半値周波数 $$0.4\pi$$ ラジアン/サンプルをもつ 3 次のバタワース フィルターを作成します。そのステップ応答を表示します。

[b,a] = butter(3,0.4);
stepz(b,a)

designfilt を使用して同じフィルターを作成し、そのステップ応答を表示します。

d = designfilt('lowpassiir','FilterOrder',3,'HalfPowerFrequency',0.4);
stepz(d)

楕円フィルターのステップ応答

正規化された通過帯域周波数 $$0.4\pi$$ ラジアン/サンプルをもつ 4 次のローパス楕円フィルターを設計します。0.5 dB の通過帯域リップルと 20 dB の阻止帯域の減衰量を指定します。フィルターのステップ応答の最初の 50 個のサンプルをプロットします。

[b,a] = ellip(4,0.5,20,0.4);
stepz(b,a,50)

designfilt を使用して同じフィルターを作成し、そのステップ応答を表示します。

d = designfilt('lowpassiir','FilterOrder',4,'PassbandFrequency',0.4, ...
               'PassbandRipple',0.5,'StopbandAttenuation',20, ...
               'DesignMethod','ellip');
stepz(d,50)

カスケード伝達関数のステップ応答

R2024b 以降

阻止帯域エッジ周波数が 0.4、阻止帯域の減衰量が 50 dB の 40 次ローパス チェビシェフ II 型デジタル フィルターを設計します。CTF 形式のフィルター係数を使用して、フィルターのステップ応答に含まれる最初の 64 個のサンプルをプロットします。

[B,A] = cheby2(40,50,0.4,"ctf");

stepz(B,A,"ctf",64)

通過帯域エッジ周波数が 0.3 と 0.7、通過帯域リップルが 0.1 dB、阻止帯域の減衰量が 50 dB の 30 次バンドパス楕円デジタル フィルターを設計します。CTF 形式のフィルター係数とゲインを使用して、フィルターのステップ応答に含まれる最初の 64 個のサンプルをプロットします。

[B,A,g] = ellip(30,0.1,50,[0.3 0.7],"ctf");
stepz({B,A,g},"ctf",64)

入力引数

b, a — 伝達関数の係数

ベクトル

伝達関数の係数。ベクトルで指定します。b と a によるこの伝達関数式は次になります。

$$H(z)=\frac{B(z)}{A(z)}=\frac{b_1+b_2{z}^{-1}\cdots +b_n{z}^{-\left(n-1\right)}+b_{n+1}{z}^{-n}}{a_1+a_2{z}^{-1}\cdots +a_m{z}^{-\left(m-1\right)}+a_{m+1}{z}^{-m}}$$

例: b = [1 3 3 1]/6 と a = [3 0 1 0]/3 は、正規化された 3 dB の周波数 0.5π ラジアン/サンプルをもつ 3 次のバタワース フィルターを指定します。

データ型: double | single
複素数のサポート: あり

B,A — カスケード伝達関数 (CTF) 係数

スカラー | ベクトル | 行列

R2024b 以降

カスケード伝達関数 (CTF) 係数。スカラー、ベクトル、または行列として指定します。B と A は、それぞれカスケード伝達関数の分子係数と分母係数をリストします。

B のサイズは L 行 (m + 1) 列、A のサイズは L 行 (n + 1) でなければなりません。ここで、

• L はフィルター セクションの数を表します。

• m はフィルターの分子の次数を表します。

• n はフィルターの分母の次数を表します。

カスケード伝達関数の形式と係数行列の詳細については、CTF 形式によるデジタル フィルターの指定を参照してください。

メモ

A(:,1) のいずれかの要素が 1 と等しくない場合、stepz はフィルター係数を A(:,1) で正規化します。この場合、A(:,1) はゼロ以外でなければなりません。

データ型: double | single
複素数のサポート: あり

g — スケール値

スカラー | ベクトル

R2024b 以降

スケール値。実数値のスカラー、または L + 1 個の要素をもつ実数値のベクトルとして指定します。ここで、L は CTF セクションの数です。スケール値は、カスケード フィルター表現のセクション全体にわたるフィルター ゲインの分布を表します。

stepz 関数は、g の指定方法に応じて、scaleFilterSections 関数を使用してフィルター セクションにゲインを適用します。

• スカラー — この関数は、すべてのフィルター セクションにわたってゲインを均一に配分します。

• ベクトル — この関数は、最初の L 個のゲイン値を対応するフィルター セクションに適用し、最後のゲイン値をすべてのフィルター セクションに均一に配分します。

データ型: double | single

d — デジタル フィルター

digitalFilter オブジェクト

デジタル フィルター。digitalFilter オブジェクトで指定します。デジタル フィルターを周波数応答仕様に基づいて生成するには、関数 designfilt を使用します。

例: d = designfilt('lowpassiir','FilterOrder',3,'HalfPowerFrequency',0.5) は、正規化された 3 dB の周波数 0.5π ラジアン/サンプルをもつ 3 次のバタワース フィルターを指定します。

sos — 2 次セクションの係数

行列

2 次セクションの係数。行列として指定します。sos は K 行 6 列の行列で、セクション数 K が 2 以上でなければなりません。セクション数が 2 未満の場合、関数は入力を分子ベクトルとして扱います。sos の各行は 2 次 (双二次) フィルターの係数に対応しています。sos の i 行目は [bi(1) bi(2) bi(3) ai(1) ai(2) ai(3)] に対応しています。

例: s = [2 4 2 6 0 2;3 3 0 6 0 0] は、正規化された 3 dB の周波数 0.5π ラジアン/サンプルをもつ 3 次のバタワース フィルターを指定します。

データ型: double | single
複素数のサポート: あり

n — 応答を求める点の数

正の整数スカラー | 正の整数ベクトル

応答を求める点の数。正の整数スカラーまたは正の整数ベクトルとして指定します。n が正の整数スカラー (t = [0:n-1]') である場合、関数は、ステップ応答の最初の n 個のサンプルを計算します。n が整数のベクトルである場合、ステップ応答は、その整数値の時点 (0 を時間軸の原点として) のみで計算されます。

データ型: double

fs — サンプル レート

正のスカラー

サンプル レート。正のスカラーで指定します。時間の単位が秒の場合、fs は Hz で表されます。

データ型: double

出力引数

h — ステップ応答

列ベクトル

ステップ応答。列ベクトルとして返されます。stepz への入力が単精度の場合、関数によってステップ応答が単精度演算で計算されます。出力 h は単精度です。

t — サンプル時間

ベクトル

サンプル時間。ベクトルとして返されます。

詳細

カスケード伝達関数

IIR デジタル フィルターをカスケード セクションに分割すると、数値安定性が向上し、係数の量子化誤差の影響を受けにくくなります。L 個の伝達関数 H₁(z)、H₂(z)、…、H_L(z) による伝達関数 H(z) のカスケード形式は次のとおりです。

$$H(z)={\displaystyle \prod _{l=1}^L{H}_l(z)}=H_1(z)\times H_2(z)\times \cdots \times H_L(z).$$

CTF 形式によるデジタル フィルターの指定

解析、可視化、信号フィルター処理で使用するため、CTF 形式でデジタル フィルターを指定できます。係数 B と A をリストしてフィルターを指定します。スカラーまたはベクトルの g を指定することで、セクション全体にフィルターのスケーリング ゲインを含めることもできます。

フィルター係数

係数を L 行の行列

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1,m+1}\\ b_{21}& b_{22}& \cdots & b_{2,m+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{L1}& b_{L2}& \cdots & b_{L,m+1}\end{array}\right],A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1,n+1}\\ a_{21}& a_{22}& \cdots & a_{2,n+1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{L,n+1}\end{array}\right],$$

として指定した場合、L 個のカスケード伝達関数のシーケンスとしてフィルターを指定したものとみなされます。このとき、フィルターの完全な伝達関数は次のようになります。

$$H\left(z\right)=\frac{b_{11}+b_{12}{z}^{-1}+\cdots +b_{1,m+1}{z}^{-m}}{a_{11}+a_{12}{z}^{-1}+\cdots +a_{1,n+1}{z}^{-n}}\times \frac{b_{21}+b_{22}{z}^{-1}+\cdots +b_{2,m+1}{z}^{-m}}{a_{21}+a_{22}{z}^{-1}+\cdots +a_{2,n+1}{z}^{-n}}\times \cdots \times \frac{b_{L1}+b_{L2}{z}^{-1}+\cdots +b_{L,m+1}{z}^{-m}}{a_{L1}+a_{L2}{z}^{-1}+\cdots +a_{L,n+1}{z}^{-n}},$$

ここで、m ≥ 0 はフィルターの "分子次数"、n ≥ 0 は "分母次数" です。

• B と A の両方をベクトルとして指定した場合、基になるシステムは 1 つのセクションから成る IIR フィルター (L = 1) であるとみなされます。このとき、B は伝達関数の分子を表し、A はその分母を表します。

• B がスカラーの場合、フィルターは全極 IIR フィルターのカスケードであるとみなされます。このとき、各セクションの全体的なシステム ゲインは B に等しくなります。

• A がスカラーの場合、フィルターは FIR フィルターのカスケードであるとみなされます。このとき、各セクションの全体的なシステム ゲインは 1/A に等しくなります。

メモ

• 2 次セクションの行列をカスケード伝達関数に変換するには、sos2ctf 関数を使用します。

• 零点-極-ゲイン フィルター表現をカスケード伝達関数に変換するには、zp2ctf 関数を使用します。

係数とゲイン

全体的なスケーリング ゲイン、または係数値から共通因数としてくくりだされた複数のスケーリング ゲインがある場合、係数とゲインを {B,A,g} 形式の cell 配列として指定できます。フィルター セクションのスケーリングは、固定小数点演算を使用して各フィルター セクションの出力の振幅レベルを確実に同等にする場合に特に重要であり、数値精度の制限によるフィルター応答の不正確さを回避するのに役立ちます。

ゲインは、全体的なゲインを表すスカラー、またはセクションのゲインを表すベクトルとして指定できます。

• ゲインがスカラーの場合、その値はすべてのカスケード フィルター セクションに均一に適用されます。

• ゲインがベクトルの場合、カスケード内のフィルター セクションの数 L よりも 1 つ多い要素をもたなければなりません。最初の L 個のスケール値はそれぞれ対応するフィルター セクションに適用され、最後の値はすべてのカスケード フィルター セクションに均一に適用されます。

係数行列とゲイン ベクトルを

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1,m+1}\\ b_{21}& b_{22}& \cdots & b_{2,m+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{L1}& b_{L2}& \cdots & b_{L,m+1}\end{array}\right],A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1,n+1}\\ a_{21}& a_{22}& \cdots & a_{2,n+1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{L,n+1}\end{array}\right],g=\left[\begin{array}{ccccc}{g}_1& g_2& \cdots & g_L& g_{\text{S}}\end{array}\right],$$

として指定した場合、フィルター システムの伝達関数は次であるとみなされます。

$$H\left(z\right)=g_{\text{S}}\left(g_1\frac{b_{11}+b_{12}{z}^{-1}+\cdots +b_{1,m+1}{z}^{-m}}{a_{11}+a_{12}{z}^{-1}+\cdots +a_{1,n+1}{z}^{-n}}\times g_2\frac{b_{21}+b_{22}{z}^{-1}+\cdots +b_{2,m+1}{z}^{-m}}{a_{21}+a_{22}{z}^{-1}+\cdots +a_{2,n+1}{z}^{-n}}\times \cdots \times g_L\frac{b_{L1}+b_{L2}{z}^{-1}+\cdots +b_{L,m+1}{z}^{-m}}{a_{L1}+a_{L2}{z}^{-1}+\cdots +a_{L,n+1}{z}^{-n}}\right).$$

ヒント

• スケーリング ゲインを含むフィルターを CTF 形式で取得できます。butter、cheby1、cheby2、ellip などのデジタル IIR フィルター設計関数の出力を使用します。これらの関数で、"ctf" フィルタータイプ引数を指定し、スケール値を取得するために B、A、g を返すように指定します。 (R2024b 以降)

アルゴリズム

stepz では、以下のコマンドを使用して長さ n のステップ シーケンスがフィルター処理され、

filter(b,a,ones(1,n))

stem を使用して、結果をプロットします。

長さを自動設定する場合に n を計算するために、stepz では、FIR の場合は n = length(b) を使用し、length(a) が 1 より大きい場合は p = roots(a) を使用して極をまず検出します。

フィルターが不安定な場合、n は最大の極をもつ項が元の値の 10⁶ 倍に達する位置に存在するものとして選択されます。

フィルターが安定している場合、n は、振幅が最大の極をもつ項が元の振幅の 5 × 10^–5 倍になる位置に存在するものとして選択されます。

フィルターが振動する (単位円上の極のみ) 場合、stepz では、最も遅い振動の周期の 5 倍が n とされます。

フィルターに振動項と減衰項の両方が含まれている場合は、発振が最も遅くなる 5 周期、または、(単位でない) 最大の振幅の極をもつ項が元の振幅の 5 × 10^–5 倍になる値の、いずれか大きい方に n が選択されます。

stepz では、分子多項式に遅延を含むことができます。遅延の数は、サンプル数の計算に組み込まれています。

参照

[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• stepz 関数に CTF 係数を入力する場合、コードを生成するには、stepz 構文に "ctf" 入力引数を含めなければなりません。

• stepz への最初の入力は、コンパイル時に可変サイズの行列である場合、実行時にベクトルにしてはなりません。

バージョン履歴

R2006a より前に導入

R2024b: カスケード伝達関数を使用したフィルターの解析

stepz 関数は、カスケード伝達関数 (CTF) 形式の入力をサポートします。

参考

アプリ

• フィルター アナライザー | フィルター デザイナー

関数

• ctffilt | designfilt | digitalFilter | freqz | grpdelay | impz | phasez | zplane